微张力算法在活套控制中的应用
2019-09-03于景辉赵德琦
于景辉,赵德琦
(1马鞍山钢铁股份有限公司 制造部,安徽 马鞍山243000;2北京科技大学设计研究院有限公司,北京 100083)
1 前言
众所周知,张力是连轧过程的一个重要现象,各机架通过带钢张力传递影响、传递能量而互相发生联系。张力是由于机架间速度差而产生的,从两个机架间来看,如果由于某种原因(外扰量或调节量变动时)而使i号轧机带钢出口速度减小(可能是轧辊速度减小,也可能是由于压下率等其他工艺参数变动,造成前滑量减小),结果使i号和i+1号机架间的带钢拉直而产生张力[1]。在轧制某些规格的带钢时,精轧区域过程控制级(简称L2)向基础自动化级(简称L1)下发的设定由于计算的秒流量不匹配造成前后机架压下率或者速度不匹配。通常这种前后机架压下率或者速度设定不匹配的情况会引起机架间带钢套量过大或者过小,后者俗称“拉钢”。而拉钢现象明显体现于前后机架穿带后电流相差过大(后机架>前机架),活套角度低于正常设定角度。当带钢对活套施加一定外力情况下,传统的液压活套油压传感器检测计算得到的带钢张力就不能反映真实的带钢张力。
针对这种拉钢现象,在某带钢热连轧现场利用传统的微张力算法对其进行简化得到一种新的带钢张力检测方法,通过这种方法判断当前是否处在拉钢现象并及时对活套高度闭环做出补偿,在一定程度上缓解了由于拉钢引起的带钢头部拉窄拉薄等不良现象。
2 活套控制系统构成与拉钢问题
在传统的活套控制策略中,活套的高度是闭环调节的,张力由于缺乏有效的检测手段,一般是开环控制。本系统中,保证张力恒定,根据活套机械结构(见图1),通过检测活套驱动液压缸两侧(无杆腔,有杆腔)油压得到的液压力矩计算得到实际带钢张力:

式中:MT为活套张力矩;FHydraulic为液压缸力;Y为液压缸作用力的垂直方向与活套动力臂的夹角;MS为带钢自重力矩;Ml为活套自重力矩。而FHydraulic可以由公式(2)计算得到:

式中:PO为无杆腔油压;PI为有杆腔油压;SO为无杆腔面积;SI为有杆腔面积。

图1 活套机构动力示意图
通过以上两式能够反算得到带钢张力,实际带钢张力与二级模型设定带钢张力形成张力闭环控制。本系统的活套控制器由位置闭环、张力闭环和高度闭环3个闭环组成。如图2所示,活套在等待过钢时处于位置闭环,根据上下游机架的负荷继电器信号切换到张力闭环和高度闭环。而高度闭环投入的时间则通过是否建张来判定。活套高度闭环与张力闭环之间相互独立,高度闭环通过设定角度换算的套量和实际角度换算的套量之间的偏差调节上游机架的速度达到套量恒定。张力闭环则通过油压传感器检测计算到的带钢张力与设定张力比较从而维持带钢张力恒定。
在轧制某些规格(极厚)的带钢时,精轧区域L2向L1下发的设定由于计算的秒流量不匹配造成前后机架压下率或者速度不匹配。“拉钢”现象直观体现于前后机架间的活套实际角度低于正常设定角度,如图3所示。拉钢现象的危害是显而易见的,当出现拉钢后,带钢头部往后的一段距离的厚度同样被拉薄。

图2 活套控制系统示意图

图3 拉钢现象
3 微张力算法建模与补偿
当轧制处于拉钢的状态时,活套系统的实际带钢张力与角度如图4所示。由图4可知,7#活套处于拉钢的状态时,活套角度(套量)远低于设定值。而通过油压传感器检测计算得到的带钢张力在曲线中却一直处于设定值范围。此时油压传感器已不能反映真实的带钢张力,而实际的带钢张力在拉钢区域要比设定值大。

图4 活套角度与带钢张力
在现场活套辊没有测压头同时传统的油压传感器检测计算方式又不能真实反映带钢张力的情况下,是否能够找到另外一种方法准确得到真实的带钢张力,很多书籍及资料中利用微张力算法进行小张力轧制。但是这种算法需要计算大量且复杂的过程参数,同时仅适用于速度较慢的机架。
对活套上游机架的主电机建立电机负载模型如图5所示。
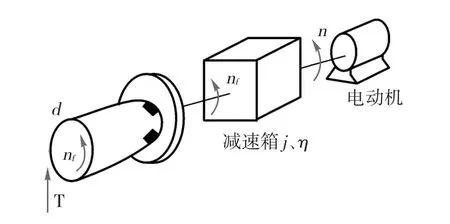
图5 电机负载模型
通过已知的电机转速n,电机功率P,经过减速箱的转速nf,减速比j、实际电机效率η以及工作辊直径d,由公式(3)~(7),可以推导出公式(8):

式中:σ为带钢张应力,n/mm2;Pm为上游机架实时输出功率,kW;η为上游机架各级传动效率;j为上游机架减速比;B为上游机架出口宽度,mm;h为上游机架出口厚度,mm;n为上游机架电机转速,r/min;d为上游机架工作辊直径,mm。
根据式(3)中计算得到的结果就能够通过电机的信息得到实际的带钢张力/张应力。针对拉钢这种现象,可以根据实际带钢的张力/张应力对高度闭环进行相应的补偿。图6即为针对高度闭环进行补偿的算法原理图,设定张力与主电机实际功率计算得到的带钢相张力比较的结果首先进入折线控制器中,而折线控制器能够输出非线性的补偿,只针对正向偏差输出即拉钢的情况才会输出,随后乘以一定的增益(可调)后为避免振荡,最终的输出要经过积分。

图6 补偿算法
补偿算法的输出量和原高度闭环控制器的输出叠加进入上游机架主传动装置。如此,一旦发生拉钢的现象,在L1(一级基础自动化)系统中会调节对应的上游机架主传动系统速度,从而让活套抬起至设定角度。
4 应用效果
为验证算法的有效性,在某带钢热连轧现场将此算法投入。将算法中的比例增益K=1,积分时间TN=5 000 ms,根据现场发生的实际拉钢现象投入。投入前后的效果对比如图7和图8所示。
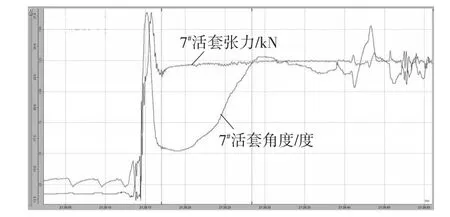
图7 算法投入前

图8 算法投入后
对比图7和图8,首先可以看出当通过检测电机功率计算得到的带钢张力>设定张力时带钢处于拉钢状态,而通过油压传感器检测计算得到的带钢张力不能反映带钢的真实张力;其次高度闭环的输出相比较算法投入前也更加快速,活套从被拉低的角度恢复到设定角度的时间也大大缩短。而带钢头部的宽度厚度相比投入前也有明显的改善,如图9所示。
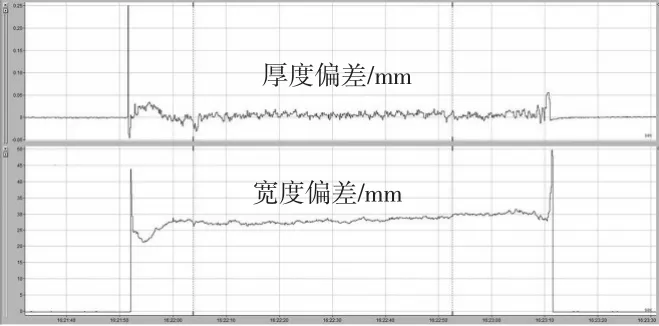
图9 算法投入后的带钢质量
5 结语
利用主电机的信息对传统的微张力算法进行改进,建立简易带钢张力模型。同时针对L2设定误差造成拉钢的现象对活套系统中高度闭环进行及时补偿,证明这种思想有利于拓展活套控制系统中对于张力检测的手段。传统的油压传感器检测在某些场合不能准确有效的反映实际带钢张力,而压头的成本又相对较高,因此本文所提出来的算法可以作为一种新的有效检测手段。笔者在某带钢热连轧现场投入使用取得了一定的效果,但该算法还需要进一步的改进,才能最终保证算法的准确性。
