无需重线性化的NTRU型全同态加密方案*

汤殿华 ， 曹云飞

（1.保密通信重点实验室，四川 成都 610041；2.中国电子科技集团公司第三十研究所，四川 成都 610041）

0 引 言

全同态加密是一种功能强大的加密技术，能够在加密数据上执行任意的计算，同时将对应的计算映射到相应的明文中，其计算结果是为密文。可以说，全同态加密技术能够全密态处理数据。采用该加密技术，用户可以将数据以加密形式外包给任何不可信服务器进行“密文计算”来获取服务，保证数据安全。全同态加密技术具有广阔的应用前景，例如云安全、加密数据库、大数据安全、搜索引擎的加密询问等。

同态密码技术对我们并不陌生，例如RSA[1]、ElGamal[2]、Paillier[3]等加密方案。这些加密算法都具有同态性，但只有单个同态运算性质，不能同时具有“加同态”和“乘同态”，以致不能够执行任意的密文计算。1978年，Rivest，Adleman，Dertouzos[4]首次提出了“隐私同态”的概念，希望解决密文任意计算问题。直至2009年，Gentry基于理想格提出了第一个全同态加密方案[5]，实现了“隐私同态”的构想。

采用Gentry的设计方法，后续出现了许多全同态加密方案。按照方案设计类型可以分为整数型[6]、GGH型[7]、Regev型[8-9]、NTRU型[10]。这些方案都引入的噪声，随着同态操作的进行，噪声将增大，当噪声规模超过某个门限值时，将不能被正确解密。因此，噪声管理是全同态密码研究的一个重点问题。

在BLLN方案[10]的基础上，基于NTRU加密方案，我们提出了一个全同态加密方案。与同类NTRU方案相比，该方案去除了重线性化算法，并且具有更为简洁的同态操作，更小的噪声增长率。

1 准备知识

1.1 符号定义

对于一个非零正整数q，令模值为q的剩余类所构成的整数环为ℤq。当q为奇数时，ℤq的元素集合表示为(-q2,q2]∩ℤ；当q为偶数时，ℤq元素集合表示为(-q2,q2]∩ℤ。特别当q=2时，ℤq元素集合为{0,1}。

对于一个实数z和一个整数t，用qt(z)表示z除以t的商，rt(z)∈(-t/2,t/2)表示余数。即qt(z)=也用 [z]t表示rt(z)。

除特殊说明外，一般使用a=(a0,a1,…,an-1)表示列向量，b=[b0,b1,…,bn-1]表示行向量。

我们将在整系数多项式环R= ℤ [x]Φd(x)上进行构造方案，其中Φd(x)为d阶分圆多项式，一般选择为Φd(x) =xd/2+1，其中d= 2m,m∈ℕ，为了方便令n=d/2。令q是非零正整数，定义表示Rq上所有可逆元素组成的集合。

令D1和D2为离散集合E上的概率分布。则他们的统计距离表示为我们用z←D表示从分布D随机抽样一个随机变量。

给定Rq上一个元素u(x)=u0+u1x+…+un-1xn-1，可以将其写成向量形式u=(u0,u1,…,un-1)，其2-范数为和无穷范数为（未做特别说明，||u||都表示为u的无穷范数）。R上的乘法扩展因子

1.2 离散高斯分布

离散高斯分布广泛用于格基密码方案的设计，尤其是基于错误学习问题（Learning With errors problem，LWE）和环上的错误学习问题（Ring Learning With Errors problem，RLWE）问题的密码方案。下面给出有关离散高斯分布相关概念。

均值为0且方差为σ2的正太分布N(0,σ2)，其概率密度函数为对于1个n实数域上的向量x∈ℝn，一个正实数s＞0，令函数由于则v=ρ/sn ss是一个∈ℝn上的概率密度函数。对于一个可数集合定义对于任何一个向量定义是对ρs(x)进行一个向量c的平移。

定义1B有界分布。如果分布χ满足：Pre←χ[|e|＜B]≤1-negl(n)。则称其为B有界分布。

对于均值为0，方差为σ2的高斯分布N(0,σ2)，成立不等式那么当k＞9.2时即高斯分布式一个有界分布。同理离散高斯分布DZn,σ也是一个有界分布，可以取界B=9.2σ。

1.3 RLWE问题

首先定义一个分布As,χ：设χ是Rq上的一个分布，此处χ一般将取为离散高斯分布。令s∈Rq，a←Rq为随机均匀选取，随机抽样一个错误e←χ，计算b=a·s+e，则得到两个环元素(a,b)所构成的新分布定义为As,χ。同时将Rq×Rq上的均匀分布定义为U。

Lyubaskevsky，Peikert和 Regev提出了 RLWE问题[11]，并将此困难问题归约到多项式环理想格中的近似最短向量问题（Shortest Vector Problem，SVP）。下面给出其定义：

定义 2 判别 RLWE 问题假设：DRLWEn,q,χ。由 (a,b=a·s+e)产生的分布As,χ与Rq×Rq上的均匀分布U是计算不可区分的，即As,χ≈U。

当s取自分布χ时，DRLWEn,q,χ仍然是一个困难问题。

1.4 DSPR问题

Stehle和Steinfeld在研究NTRU的可证明安全性时， 研究了DSPR问题[12]（Decisional small Polynomial Ratio Problem），并得出q为素数，分圆多项式环条件下，h=g/f（g、f取自离散高斯分布χ）所形成的分布与Rq上的均匀分布是不可区分的。微软研究中心的Joppe W. Bos等人将该DSPR进行了推广[10]。

定义4 DSPR问题：DSPRn,q,χ。对于安全参数为λ，n、q为整数，为Rq上的分布，令即t为Rq上的可逆元素。则DSPRn,q,χ问题为：h=(y1+t·χz1)/(y2+t·χz2)modq所形成的分布与Rq上的均匀分布是不可区分的。

一般χ为分布表示限制于上的离散高斯分布Dℤn,σ。DRq,σ表示限制于Rq上的离散高斯分布Dℤn,σ，该分布可以对每个系数采用Dℤn,σ抽样来获得。

定理1 令d≥8是一个2的幂，q≥5是一个素数，令Φd(x)=xd/2+1，设Φd(x)在模q上可分解为个不可约多项式因子令表示中心为z∈Rq的离散高斯分布则分布与均匀分布的统计距离为：

由定理1可知，通过设置参数可以保障h和两个分布的统计距离可忽略，并且推断出h=g/f（g、f取自离散高斯分布χ）所形成的分布与是统计不可区分的。

1.5 同态加密方案的定义

定义5 同态加密方案。一个同态加密方案是概率多项式时间算法的一个四元组HE=（KeyGen，Enc，Dec，Evaluate），如下：

KeyGen：根据安全参数λ，生成方案的私钥sk、公钥pk、计算公钥evk。

Enc：给出一个明文m，用公钥pk加密明文m，得到密文c。

Dec：输入私钥和密文c，进行解密运算，输出明文m´。

Evaluate：输入公钥pk，t输入线电路Cir，一组密文c=(c1,c2,…,ct)，其中。ci=Encpk(mi),i=1,2,…,t输出c*=Evaluate(pk,Cir,c)，且以极大的概率满足Dec(sk,c*)=Cir(m1,m2,…,mt)。

既然同态加密能够对密文进行计算，那么需要对其密文计算的程度进行衡量。也就是Evaluate算法所支持的运算集合。

定义6C -同态。设C是一个电路集合，HE是一个同态加密方案，任取一个电路Cir∈C，设其输入线有t个。如果对任意的一组明文m1,m2,…,mt和所对应的一组密文c=(c1,c2,…,ct)（其中ci=Encpk(mi),i=1,2,…,t），有下面的等式成立：

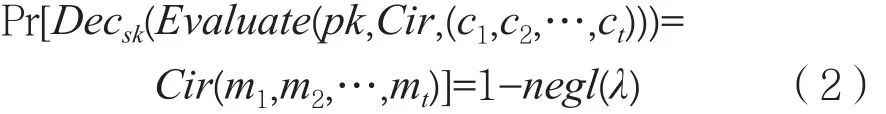
则称该方案为C-同态，或者方案对于一个电路集合C 是正确的，同时也称C为方案HE的可许电路集合，当C是一个有限电路集合时，也称方案为类同态加密方案。

定义7 紧同态加密。如果存在一个多项式g=g(λ)，使得HE方案的Evaluate算法的输出比特长度不超过g。则称HE是一个紧同态加密方案。

注意：g与所运算的电路Cir、输入密文数无关。表明随着同态操作的进行，密文的尺寸始终保持在一个界之内，其尺寸独立于同态操作数。

定义8 紧运算。如果HE是紧的且对电路集合C 是正确的。称该同态加密方案HE紧运算C 中的电路。

定义9 全同态加密方案。一个方案HE对所有的电路既是紧的，又是同态的，则称其是一个全同态加密方案。

定理2 自举转化定理。如果一个同态加密方案HE能够同态计算自身的解密电路，并且之后还能计算一个乘法电路，HE方案满足循环安全，那么该方案可以转化为一个全同态加密方案。

1.6 比特分解算法与比特分解逆算法

整数环ℤq上的数b∈ℤq，可以表示成比特长度为l= ⌊logq⌋+1的二进制数据(bl-1bl-2…b0)2，将其按住从低位到高位的顺序写成l维向量(b0,b1,…,bl-1)。

对于b∈ℤq，其比特分解算法BD，规定为：

同理，对于n维向量其比特分解算法BD，规定为：BD(a)=(BD(a0),BD(a1),…,BD(an-1))，即 BD(a)=(a00,a01,…,a0,l-1,a10,a11,…,

可以将BDI写成矩阵表达的形式为：

对于m×n阶矩阵其比特分解算法BD和比特分解逆算法BDI类似。即将每一行看着1个n维向量处理，然后调用向量的BD和BDI算法。

令c∈Rq，其比特分解算法规定为：BD(c)=

令Rq上的l维向量c=(c0,c1,…,cl-1)，则其比特分解逆算法BDI，规定为

令Rq上的m维向量则比特分解算法BD，规定为BD(c)=(BD(c0),BD(c1),…,BD(cm-1))。类似可以定义Rq上向量的比特分解逆算法，以及Rq上矩阵的比特分解算法和逆分解算法。

特别地， 对于Rq上的l单位矩阵Il×l，BDI(Il×l)=(1,2,…,2l-1)。 则对于c∈Rq，有同理对于同样有

2 全同态加密方案

2.1 类同态加密方案NSHE

本小节基于RLWE问题和DSPR问题提出了一个NTRU型的类同态加密方案（Somewhat Homomorphic Encryption），命名为NSHE方案。该方案具有一定深度的同态计算能力，并且其密文计算算法形式简单，不需要重线性化算法来控制密文尺寸增长。基于此同态加密方案，可以利用自举转化定理进一步构造全同态加密方案。令本方案的运算均为上的运算，下面将给出类同态加密方案的具体描述。

SH.KeyGen(1λ)：输入安全参数λ，生成分圆多项式环离散高斯分布和为明文空间的模值，则明文空间为：在离散高斯分布上随机选择f´←DRq,σkey，令f=t·f´+1，并检测f是否可逆。如果不可逆，重选择f´，止到选择出可逆的f。计算f-1，然后随机选择计算

SH.Enc(m,pk)：输入消息m∈Rt，随机选择根据公钥pk=h计算：

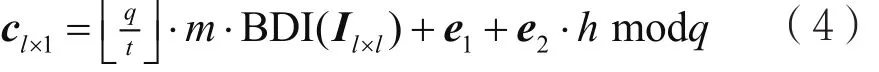
其中Il×l为l阶单位矩阵。

SH.Dec(c,sk)： 输入密文cl×1=(c0,c1,…,cl-1)， 使用私钥sk=f进行解密，

SH.Add(c,c´)： 输入两个密文c,c´， 计算

SH.Mult(c,c´)：输入两个密文c,c´和计算密钥evk。计算最后得到

2.2 解密正确性条件

定理3 令密文c是由本方案SH.Enc(m,pk)所产生，令e2,0·g，则本密文c能够被正确解密的条件为：

证明：根据类同态加密方案的解密算法，存在多项式向量kc´∈R，使得成立如下等式：

令v=e1·f+e2·g，kc=kc´·f-e2·kg，v,kc为l维列向量。由2.6节可知，BDI(Il×l)=(1,2,…,2l-1)。由于Δ·t=q-rt(q)，f=t·f´+1 则有：

进一步得到：

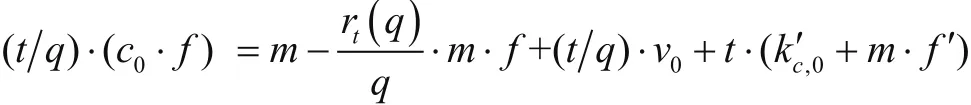
可以进一步推广定理3的结论，得到定理4。

定理4 设经过同态操作后的密文或者由SH.Enc(m,pk)产生的密文c，其存在这样的表达式(t/q)·(c·f)=m·BDI(Il×l)+v+t·kc，其中那么c能够被正确解密的条件为：

对于密文c，称(t/q)·(c·f)表达式中的v为噪声，噪声大小为||v0||∞。

那么由SH.Enc(m,pk)直接产生的密文c的噪声为其噪声规模为

2.3 同态操作的噪声分析

由于密文中含有噪声，那么随着同态加法和同态乘法操作进行，密文中的噪声不断地在增大，一旦噪声的规模不满足解密正确性条件，将导致解密错误。下面分析同态加法和同态乘法的噪声增长率，令两个输入密文c、c´，且在代入私钥sk=f时具有如下表达形式：

存在kc,kc´∈Rl，使得成立：

设这两密文的噪声规模分别为E、E´。根据t·kc=(t/q)·(c·f)-m·BDI(Il×l)-v， 可以推断出

（1）同态加法

由于密文c、c´所对于的消息m∈Rt、m´∈Rt，其消息在Rt加法运算为m+m´=[m+m´]t+radd·t，||radd||≤1。由同态加法算法SH.Add(c,c´)可知，存在kAdd∈Rl使得cAdd=c+c´+q·kAdd。则有：

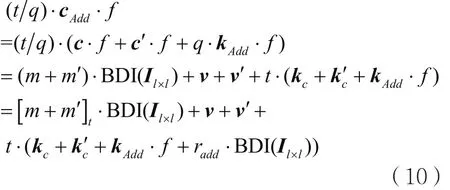
由以上运算可以得出cAdd的噪声项为vAdd=v+v´。则其噪声规模为EAdd=||v0+v0´||∞≤E+E´。

（2）同态乘法

同态乘法的噪声分析相对较为复杂。令消息m∈Rt、m´∈Rt在Rt上的乘法运算为m·m´=[m·m´]t+t·rMult，||rMult||≤δR·t/4+1/2。根据同态乘法，存在kM,kr∈Rl， 成立cMult=BD(c´Mult)·r+q·kM，则有：

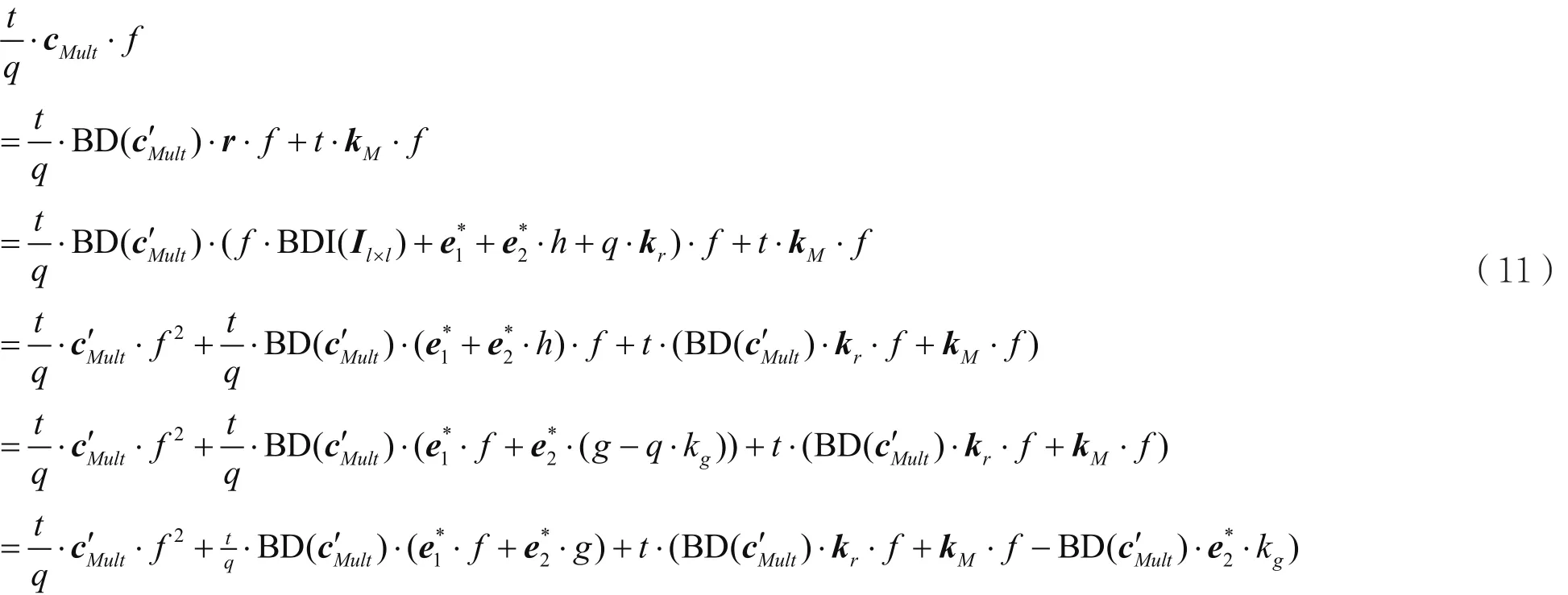
那么：

综上所述，所得：

则密文cMult的噪声为：

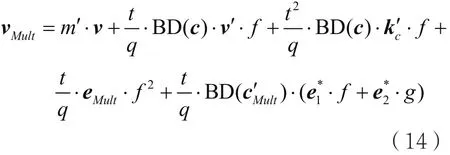
根据分析可知密文c´中噪声分量的规模都是小于E´，c的情况也一样，因此cMult噪声规模为：

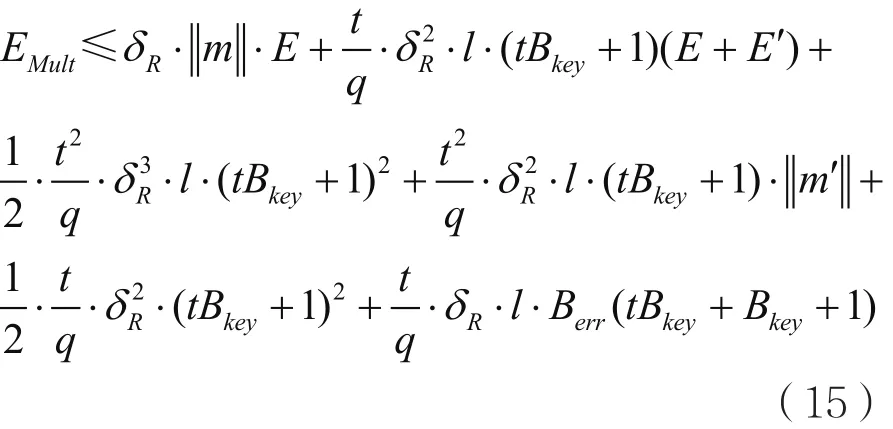
由同态加法和同态乘法操作的噪声分析可知。同态加法的噪声增长比较小，可粗略看为两个密文的噪声相加；同态乘法的噪声增长较大，可粗略看为两个密文噪声的线性组合。综上所述，本方案的同态操作的噪声增长均为线性。

2.4 同态计算能力

定理4类同态加密方案NSHE能够同态计算的电路深度L满足以下条件：

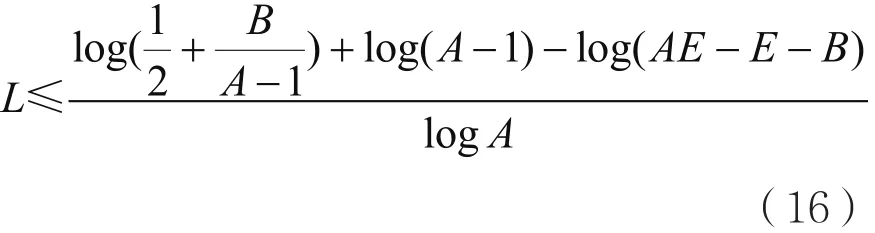
其中：

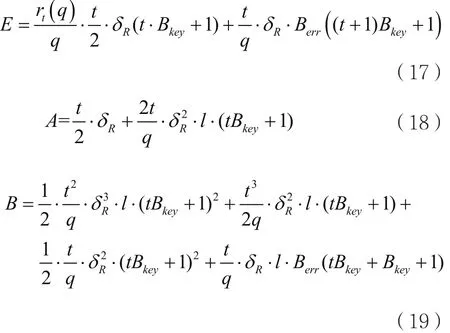
证明：根据同态操作的噪声分析，可以看出“同态乘法”所引入的噪声比“同态加法”要大很多，所以我们粗略地使用“方案能够计算的乘法深度”来作为方案能够同态计算的电路深度。

由类同态加密方案NSHE可知，密文的新鲜噪声规模为：

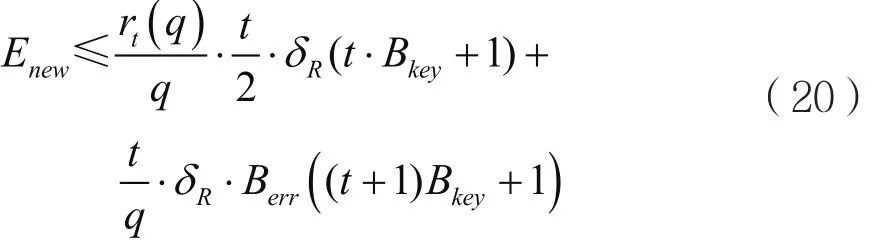
那么两个新鲜密文经过一次同态乘法之后，噪声规模为：

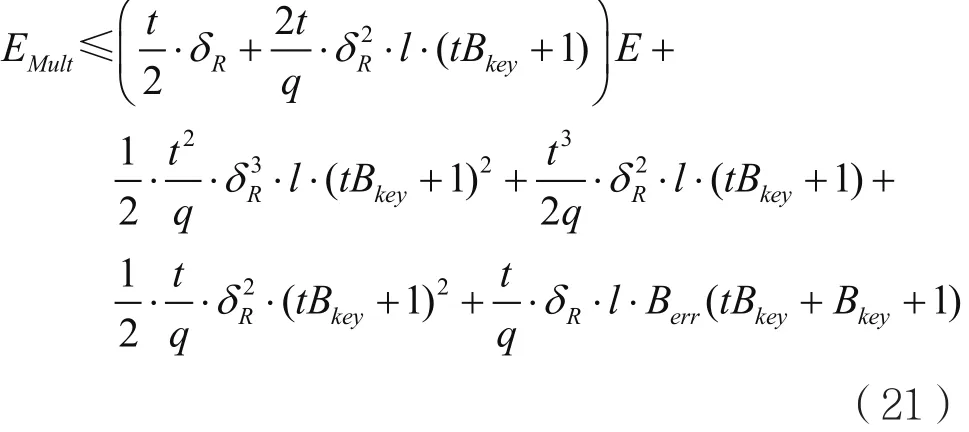
则：E1＜A·E+B。

再经过一次同态乘法，噪声规模为：E2＜A·E1+B＜A(A·E+B)+B＜A2·E+A·B+B。

依次类推，经过深度为L同态乘法，噪声规模为：

为了保证经过深度为L的同态乘法运算之后的密文能够被正确解密，那么必须满足即

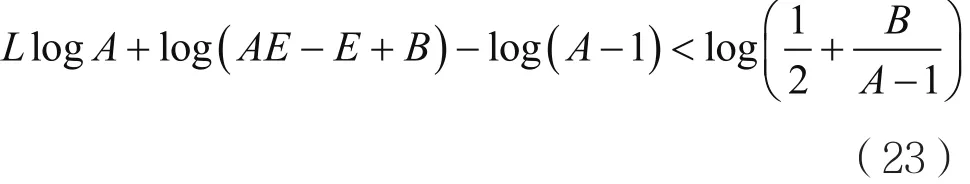
对该不等式求解，得到：

2.5 全同态加密方案

根据Gentry的自举转化定理可知，当类同态加密方案能够在满足自举性质时，可以通过自举转化定理转化为一个全同态加密方案。所谓自举性就是：类同态加密方案能够同态计算自身的解密电路，并且之后还能计算一次同态乘法。

根据文献[8]对解密结构的分析，本方案当t=2时解密电路的电路深度为：

当解密电路的深度加1后小于方案的同态计算能力时，类同态加密方案可以由自举转化成为全同态加密方案。要求成立以下不等式

类同态加密方案不天然具有自举性，必须通过一些技术，在保证其同态计算能力不变的情况下，对解密算法进行处理，降低解密算法的电路深度。

（1）方法1：采用模转换技术（Modulus Switching），降低模值q´，从而降低解密电路的深度。

（2）方法2：采用密钥转换技术（Key Switching），转换为一个更为“简单”私钥。例如非零系数项数较少，系数小的私钥f*。下面给出密钥转换技术。

密钥转换技术需要一个辅助信息ks，可以理解为在新公私钥(pk*,sk*)=(h*,f*)下，对原私钥f加密。即其中。h*=g*/f*那么密钥转换算法为：

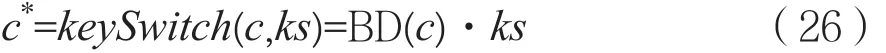
其存在kks,v*,kc*∈Rl，成立等式：

通过分析可知，c*所由私钥f*解密，对应的消息仍然为m。

3 安全性证明

本节将给出2.1节所给出的同态加密方案在vDRLWEn,m,q,χ困难问题下具有IND-CPA安全。

定理5在DRLWEn,q,χ困难问题假设下，类同态加密方案NSHE是不可区分选择明文安全的（Indistinguishability Under Chosen-plaintext Attack，IND-CPA）。

证明：采用Stehle和Steinfeld在文献[12]中的证明方法来证明方案安全性，具体如下：

令A 是一个对本方案IND-CPA攻击者。B 是一个对vDRLWEn,m,q,χ困难问题的挑战者，能够访问预先设定秘密信息s←DRql,σerr的谕言机O，返回一个U(Rq×Rql)或者As,m,χ抽样。攻击-挑战游戏模型如下：

B 访问谕言机O，获得一个抽样 (h´,c´)，令pk=h´，并将pk发送给攻击者A 。

A 在消息空间Rt中随机选择两个消息m0,m1，并发送给挑战者B 。

B随机选取一个比特b←{0,1}，计算挑战密文c=Δ·mb·BDI(Il×l)+c´，将c发送给攻击者A 。

A根据自己攻击能力，猜测b的值为b´，并将b´发送给B 。

如果b´=b，B输出1，否则输出0。

由于t在Rq上可逆，且通过DSPR问题的定理1可知，h´与真实的公钥h分布是统计不可区分的。又因为当B 访问谕言机O，响应的是一个As,m,χ抽样 (h´,c´=s·h´+e)，则c=Δ·mb·BDI(Il×l)+c´=Δ·mb·BDI(Il×l)+s·h´+e是符合真实密文分布的。因此B和A间的挑战-攻击游戏建立了正确的IND-CPA模型。vDRLWEn,m,q,χ是困难的，那么NSHE方案是满足IND-CPA安全的。

4 结 语

全同态密码由于具有密态计算功能，能够保证数据计算处理的信息安全，特别满足当前云计算，大数据的安全需求，这使得全同态密码具有广阔的应用前景。虽然全同态密码的同态操作已经处于毫秒级水平，但这仍然不能满足复杂环境的时钟级速度。因此全同态密码的效率仍然是研究的重点。我们基于NTRU提出一个全同态加密方案，与同类NTRU方案相比，该方案去除了重线性化算法，并且具有更为简洁的同态操作，更小的噪声增长率。