多终端约束条件的任意加权最优制导律
2019-09-02易文俊袁丹丹
黄 磊,易文俊,管 军,袁丹丹
(南京理工大学 瞬态物理国家重点实验室, 南京 210094)
随着现代战争形式的演变,对制导律提出了更高的要求。现代制导武器在末端实施精确打击的同时,还要求以特定的落角来打击目标的薄弱部位,以提高毁伤效果。基于此,多终端约束条件的制导律已成为国内外学者研究的热点,这些制导律在满足脱靶量为零的同时,还要求满足特定的性能指标,例如大落角、飞行时间最短、控制能量最小等。近年来,多种控制理论在制导律设计中得到应用,其中基于最优控制理论设计的制导律能得到解析的、状态反馈形式的制导指令,所以得到了广泛的应用。
文献[1]中利用拉格朗日乘子法推导出了满足单片机工作要求的限制落点与落角的最优制导律,制导律形式包含弹目视线角、弹目视线角速率、终点弹道高及终点导弹速度项,最终结果不具有一般性。文献[2]中利用线性二次型最优控制理论研究了带落角的最优制导律,这种方法虽然精度高,但计算复杂,推导公式过程比较繁琐。文献[3]中在比例导引法的基础上研究了二次型最优制导律。文献[4]中依据一阶驾驶仪动力学特性研究了带角度约束的最优制导律。为此,文献[5]中根据卫星制导炸弹的弹道特点通过求解黎卡提微分方程研究了次优制导律,一定程度上简化了计算过程,降低了推导难度。文献[6]中研究了针对侵彻制导武器的多终端约束的制导律。文献[7]利用Schwarz不等式研究了带落角约束的任意加权函数最优制导律,但对加权函数有一定的限制。文献[8]中研究了带落角约束的间接Gauss伪谱最优制导律,简化了对复杂加权函数的求解难度。文献[9]中利用最优控制理论设计了带落角约束的制导律。
本研究利用极小值原理和求解线性二次型最优控制方程,对任意加权函数进行求解,扩展了加权函数的选取范围,可根据制导目的不同,任意选取加权函数。本研究选取两种在最优控制领域最经典的加权函数进行求解,均推导出了解析形式的最优制导律,并进行了仿真验证。采用蒙特卡洛打靶发研究了风和测量误差对制导精度的影响。
1 系统模型的建立
图1为导弹末制导段弹目相对运动二维关系图,图中:M为导弹,T为目标,θm为导弹速度倾角,q为弹目视线角,θf为期望落角,vm为导弹速度,a为垂直于导弹速度方向的加速度,R为弹目相对距离。

图1 末制导弹目相对运动二维关系
由图1,可得到弹目相对运动的导引关系方程为:

(1)
式中:v为y轴方向上的速度。u(t)为制导指令。假设导弹的速度vm为常值,θm为坐标系下的小角度,则式(1)可线性化为:
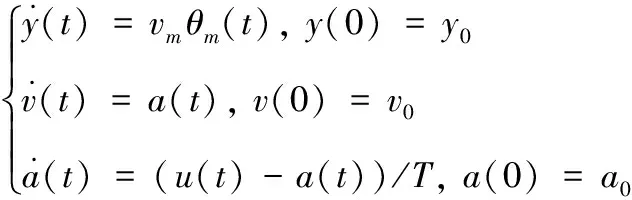
(2)
运动方程式(2)的状态方程为
(3)
式中:

(4)

(5)
由图1可知,要满足零脱靶量和终端落角要求,即满足

(6)
写成矩阵形式为
Cx(t)=D
(7)
式中
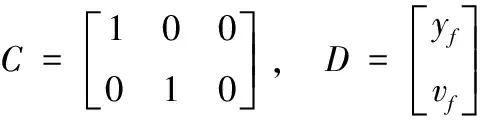
(8)
在满足上述约束条件时,寻找u(t)使得以一般函数R(t)为加权函数的控制能量最小:
(9)
由文献[10]中可知上述最优控制问题的解为:
u*(t)=R-1BTFH-1(FTx(t)-D)
(10)
式中:
(11)
(12)
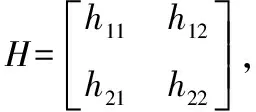
(13)
2 最优制导率的求解
2.1 R-1(t)=1的情况
2.1.1考虑控制系统为一阶惯性环节时的最优制导律
由式(12)可得到
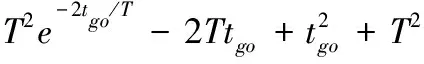
(14)
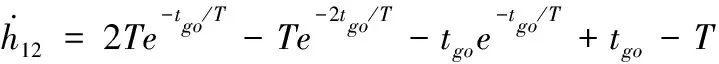
(15)
(16)
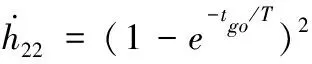
(17)
对式(14)~式(17)式分别在区间[tf,t]积分,得到
(18)

(19)
h21=h12
(20)
h22=Te-2tgo/T/2-2Te-tgo/T-tgo+3/2T
(21)
将式(18)~式(21)及式(2)、式(6)及q(t)=-y(t)/R代入式(10)得到
(K1tgo+K2)vmθm+(K1f31+K2f32)a(t)-K2vmθf]
(22)
式中,
K1=f31h22-f32h21
K2=f32h11-f31h12
(23)
2.1.2不考虑控制系统惯性时的最优制导律
当时间常数相对于飞行时间较小或者系统反应滞后较小时,可以忽略动力学系统时间常数的影响。即T→0,则
(24)
(25)
h21=h12
(26)
h22=-tgo
(27)
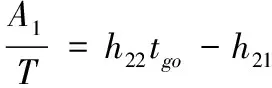
(28)
(29)
此时,式(22)变为
(30)
式(30)的结果与文献[11]和文献[12]中的带落角约束的最优控制制导律是一致的。
2.2 R-1(t)=eNtgo的情况
2.2.1考虑控制系统为一阶惯性环节时的最优制导律
此时,由式(12)可得:
(31)
Te-2tgo/T+Ntgo+tgoeNtgo-TeNtgo
(32)
(33)
对式(31)~式(33)式分别在区间[tf,t]积分,得到
(34)

(35)
(36)
将式(34)~式(36)式代入式(10)得到控制系统为一阶惯性环节时的最优制导律
(K1tgo+K2)vmθm+(K1f31+
K2f32)a(t)-K2vmθf]
(37)
式中
K1=f31h22-f32h21
K2=f32h11-f31h12
(38)
2.2.2不考虑控制系统惯性时的最优制导律
当时间常数相对于飞行时间较小或者系统反应滞后较小时,可以忽略动力学系统时间常数的影响。即T→0,则
(39)
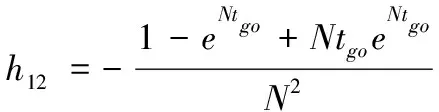
(40)
(41)
(42)
(43)
将式(39)~式(41)代入式(10)得到不考虑控制系统惯性环节时的最优制导律
(K3+h11/tgo)θm-K4θf/tgo]
(44)
式中
K3=tgoh22-h21
K4=h11-tgoh12
(45)
3 仿真分析
在本小节中对推导出来的最优制导律进行仿真验证,采用控制变量法从不同终端落角、不同初始射角、不同初始弹道高等三方面进行了验证,通过仿真数据对制导过程中的相关特性进行了全面分析。分析结果表明,本文推导的制导律满足脱靶量、大落角等性能要求。
以R-1=1为加权函数,以控制能量函数为性能函数,现有大量文献已做了较为全面的分析[13-16]。基于此,本研究只对指数加权函数下的最优制导律进行仿真分析,并分别考虑控制系统为一阶惯性环节和无惯性环节两种情况。以下将最优导引律式(44)、式(37)分别简称为OGL1和OGL2。仿真初始参数如表1所示,导航系数N=0.6,时间常数T=0.3。脱靶量和落角误差如表2所示。弹道倾角图和弹道轨迹图如图2所示。
从表2、图2可以看出在OGL1和OGL2制导律的作用下导弹都能以期望的落角去要求。从图2(b)可以看出,弹道倾角向期望落角收敛的速率较快。从图2(c)可以看出,最大制导指令出现在制导初始段,随着弹道倾角向期望落角趋近时,制导指令也会随之减小,当弹道倾角达到期望落角时,制导指令会随之趋近于0。
图3的仿真初始条件为:弹道高ym=2 800、2 600、2 400 m,落角为75°,其他参数不变。从图3(a)可以看出,不同初始弹道高在OGL1和OGL2情况下都能以预期的落角、落角击中目标,且误差满足要求。如图3(b)所示,制导初始段法向过载较大,在制导末段制导指令会趋近零,弹道倾角会以较快速度向期望落角收敛。

表1 仿真初始参数

表2 制导结果
图4的仿真初始条件为:初始弹道倾角θm0=-10°、-20°、-30°,期望落角为75°,其他仿真初始参数不变。从图4中可以看出,在OGL1和OGL2作用下均能以预期落角、落点击中目标,且误差满足要求。

图2 不同终端落角下的仿真结果

图3 不同弹道高情况下的仿真结果

图4 不同初始弹道倾角情况下的仿真结果
由于在制导末端风的干扰是客观存在的,这会对制导结果产生不利的影响,因此,研究所设计制导律的抗风干扰能力是必要的。本文以期望落角为90°为例,给导弹速度全程加上±10%的偏差,采用蒙特卡洛方法研究落点和落角误差,仿真计算200次,落点和落角仿真结果如图5所示。
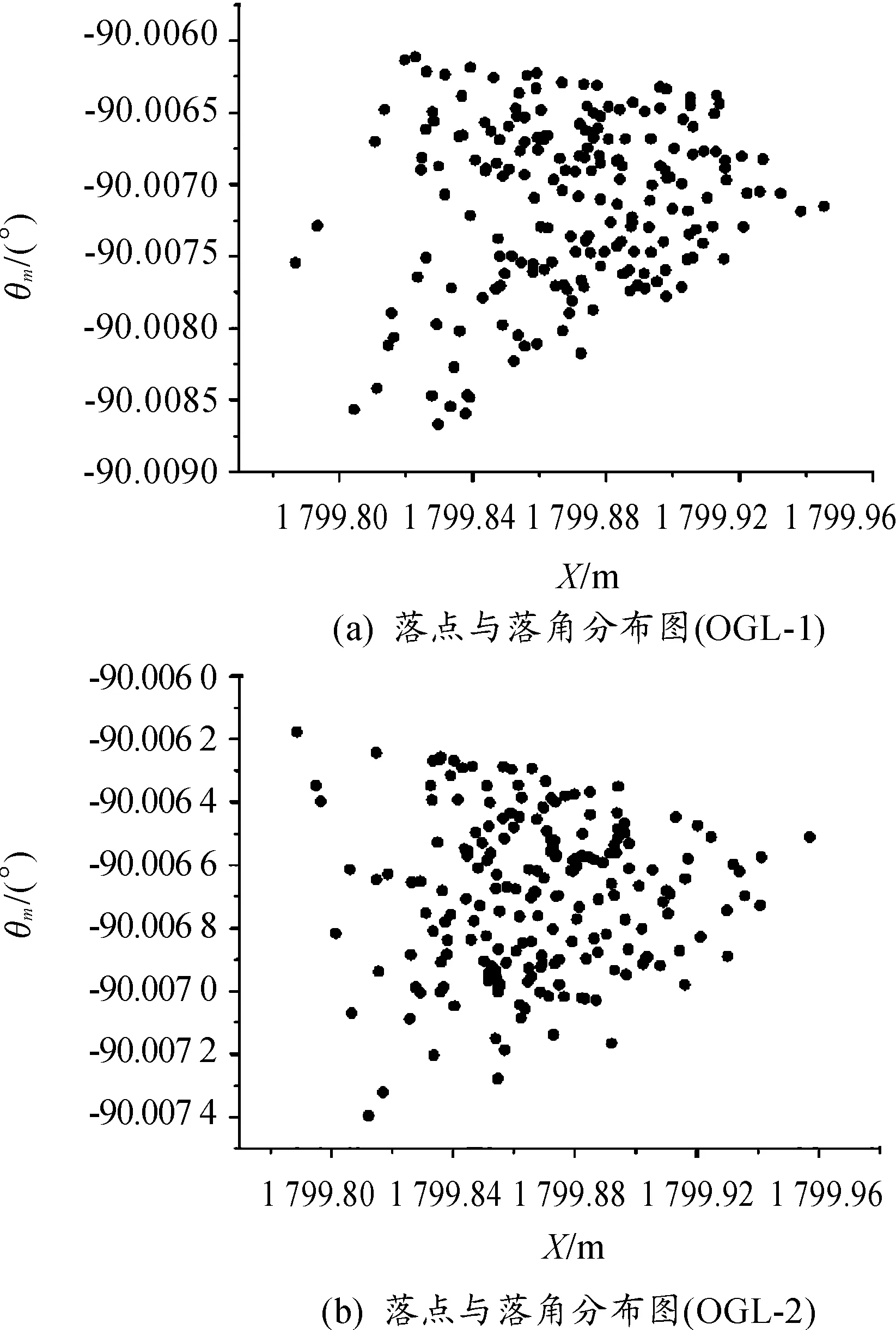
图5 考虑风的仿真结果
由图5可知,OGL-1制导律在给导弹速度全程加±10%的偏差的情况下落点误差在0.24 m以内,落角误差在0.009°以内;OGL-2制导律落点误差在0.22 m以内,落角误差在0.007 4°以内。落点和落角误差都在允许范围之内。
测量误差在末制导阶段也是客观存在的,也会对制导精度产生不利影响。对于本文两种制导律来说,主要是剩余飞行时间的估算误差会对制导精度产生影响。仿真时,考虑5%的测量误差,采用蒙特卡洛方法计算200次,落点和落角仿真结果如图6所示。
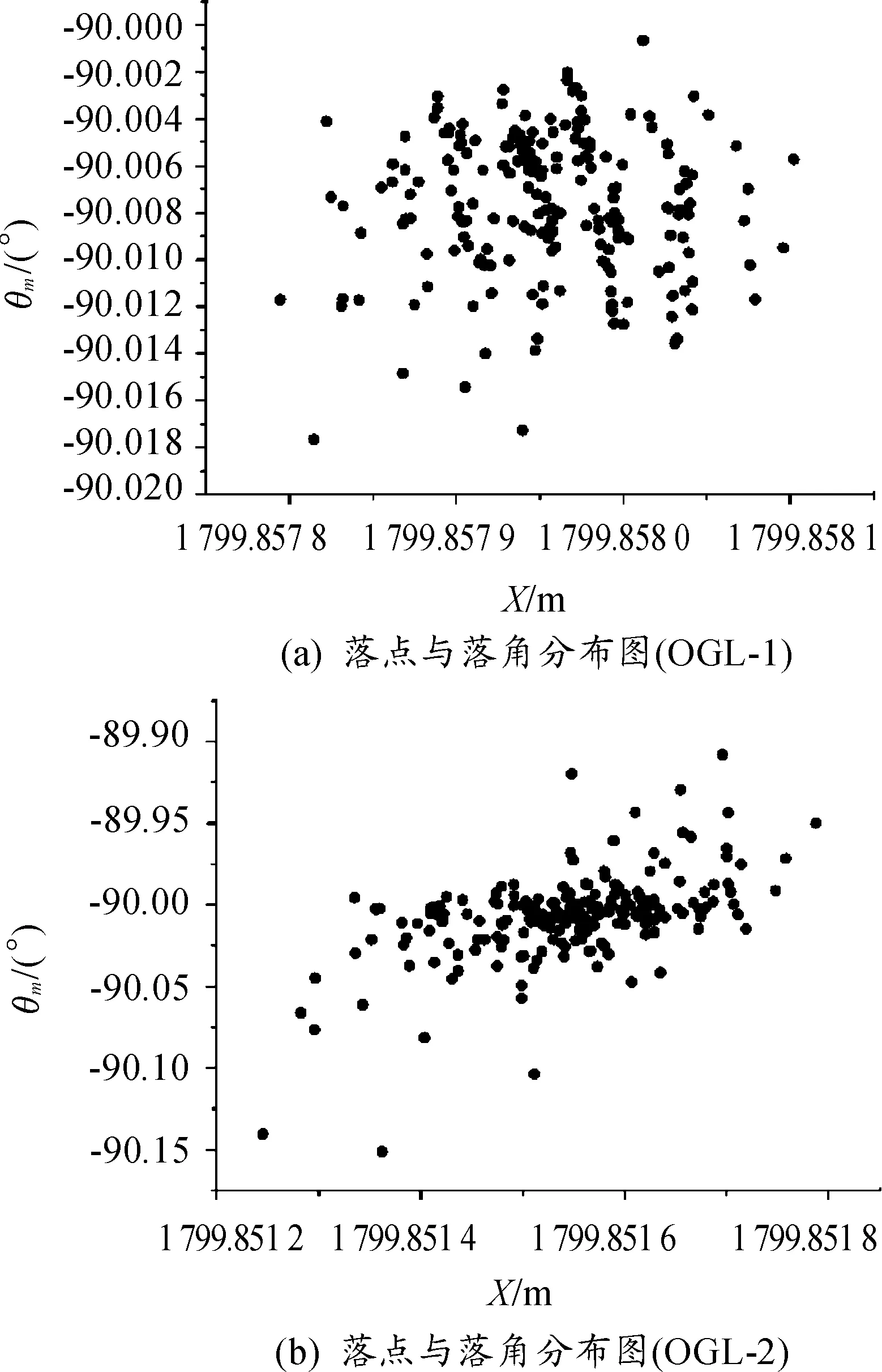
图6 考虑测量误差的仿真结果
由图6可知,在考虑5%的测量误差的情况下,OGL-0的落点误差在0.260 m以内,落角误差在0.020°以内;OGL-1最优制导律的落点误差在0.25 m以内,落角误差在0.1°以内。
4 结论
研究了多终端约束条件的任意加权最优制导律。对给定的加权函数通过本文的研究方法都能得到解析形式的最优制导率。可根据制导目的的不同,选取不同的加权函数进行求解,拓展了加权函数的选择范围。
通过本文方法推导出来的最优制导律形式简单,仅包含弹目视线角、落角、弹道倾角、法向加速度项,这些数据的获取在工程上都较容易获取,所以本文的最优制导率可为工程实践提供一定的理论指导。
拓展了指数加权函数情况下的仿真内容,采用控制变量法分别验证了制导律在不同期望落角、不同弹道高、不同弹道倾角下的准确性,分析了相关弹道特性。
在制导末端风对落点和落角的影响时,两种最优制导律在制导末端抗风能力较强。本文推导的两种带落点和落角的最优制导律稳定性较好,可靠性较高,对工程实践有一定的指导意义。
