三维裂纹扩展轨迹的厚度效应研究

赵 慧，吕 毅，窦鹏鹏

(1.西安航空学院 飞行器学院， 西安 710077； 2.西北工业大学 航空学院， 西安 710072)

工程构件和机器零部件的失效常常发生在有应力集中的裂纹位置。在载荷的作用下，裂纹一般表现为三维裂纹，这些裂纹往往会造成受力构件的强度下降甚至零件断裂。研究表明裂纹扩展对几何形状、应力和裂纹的大小及位置非常敏感，特别是三维裂纹内部具有十分复杂的应力应变场。在进行三维裂纹分析时，必须考虑三维裂纹应力应变场的影响[1]。在当前的工程分析中，普遍的做法是使用二维裂纹扩展理论或者是工程经验来对三维裂纹进行扩展预测，但是以二维断裂力学理论为基础的疲劳寿命模型往往考虑不到一些三维因素，例如构件的厚度和应力状态等。因此，研究工程结构中三维裂纹扩展轨迹的厚度效应具有重要的工程实用意义。

结构厚度对裂纹扩展轨迹有着显著的影响，近年来，国内外学者针对厚度对裂纹扩展轨迹的影响做了大量的研究。应力状态的不同是导致厚度效应的主要原因，Irwin[2]最早提出用约束效应研究裂纹扩展中的厚度影响。1981年，Newman[3]提出总体约束因子，考察了不同厚度下的裂纹尖端拘束和断裂韧性之间的关系。张晓彤[5]建立了考虑厚度效应的裂纹前缘塑性区评估公式，为含裂纹损伤构件的疲劳寿命评估提供了参考。赵凌燕等[6]认为由于裂尖拘束效应的影响，含裂纹的厚试样具有更大的裂纹扩展驱动力。张胜等[7]对不同厚度的缺口试样进行了疲劳裂纹扩展试验，并对裂纹前沿形貌进行了方程拟合，取得了与试验相符合的结果。高潮、伍黎明和何宇廷等[8]通过能量释放率的概念，对三维裂纹前缘进行了模拟仿真，取得了与试验相符合的结果。

厚度不仅仅体现在对应力状态的影响，还体现在对裂纹扩展断口形貌的影响。对于大多数铝合金材料，会发生如图1所示的裂纹扩展断口形貌。因为裂纹长短不同则裂尖应力状态不同，应力状态不同则最大剪应力所在平面就不同，最终导致断口形式不相同。因此，裂纹在疲劳载荷作用下，其断口从平面应变对应的平断口逐步转变为平面应力对应的斜断口[9]。Newman[10]对转换后的断裂参数进行研究后发现，该扩展模式的转变与结构厚度有着密切关系。

图1 裂纹扩展从拉伸模式转换为剪切模式

本研究基于ANSYS有限元软件对三维穿透裂纹结构进行参数化建模，将含裂结构分为非裂纹体和含裂纹体，对它们进行独立建模和划分网格，通过位移法求解裂纹前缘的应力强度因子，对受拉伸载荷作用的三维薄板穿透裂纹和三维大厚度板穿透裂纹进行裂纹扩展轨迹分析，揭示出厚度对于三维穿透裂纹扩展轨迹的影响规律。

1 三维裂纹扩展轨迹模拟方法

1.1 基本思路

利用有限元软件ANSYS进行裂纹扩展轨迹模拟的基本思路是：① 建立初始含裂模型；② 加载求解；③ 位移法[11]计算应力强度因子值；④ 计算裂纹扩展增量和扩展方向；⑤ 建立新的裂纹和有限元模型，并不断重复②～⑤即可实现裂纹扩展轨迹的自动扩展。

在对含有三维裂纹的结构进行有限元建模过程中，裂纹前缘通常划分出许多的结点。这些结点在复杂的受力状态以及厚度效应的影响下呈现出不同的应力应变场，所以各结点的扩展方向及扩展增量也各不相同。为了得到裂纹扩展规律，需要对裂纹前缘各个结点的扩展方向(偏转角度θ0)和扩展增量Δa进行全面分析。

1.2 确定扩展增量

在确定裂纹前缘各结点扩展增量时，先确定裂纹前缘某一结点的扩展增量，则其余结点的扩展增量可通过Paris公式[12]间接求得，Paris公式一般形式为：

(1)

式中：C、n为材料常数，一般由试验确定，且随应力比R的改变而改变；ΔK=Kmax-Kmin为应力强度因子的幅值。

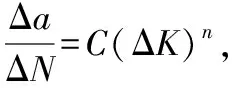
(2)

1.3 确定扩展方向

预测裂纹扩展行为的过程中存在大量的冗长计算，为了便于实际应用，Richard[14]提出了一个近似函数，该判据采用的是标准化的应力强度因子作为裂纹扩展的主要控制参量，因此避免了大量繁琐复杂的计算，有很大的工程实用价值，其中标准化的应力强度因子由式(3)～(5)计算得到：

(3)

(4)

(5)

其中，KⅠ、KⅡ和KⅢ分别为Ⅰ型、Ⅱ型和Ⅲ型裂纹的应力强度因子。

该判据定义下的裂纹扩展角按如下公式计算：

(6)

(7)

由式(6)可知，对Ⅰ型裂纹而言，当KⅡ=0时θ0=0°，裂纹将沿着原来的裂纹面扩展，不发生偏转；而对于KⅢ=0，ψ0=0°的Ⅰ-Ⅱ复合型断裂问题，裂纹扩展的方向完全由θ0确定。分析二维裂纹时，A=155.5°，B=-83.4°；分析三维裂纹时，A=140°，B= -70°。θ0的正负由Ⅱ型的应力强度因子决定，即KⅡ>0时，θ0<0°；KⅡ<0时，θ0>0°。由于本文模型不涉及Ⅲ型裂纹，对C和D的取值不再赘述。

对于本文所分析的三维穿透裂纹结构，先由位移法计算得到裂纹前缘各结点的应力强度因子值，再由Richard判据计算得到各结点的偏转角θ10,θ20…,θm0,…。

1.4 裂纹扩展程序

对于三维穿透裂纹，裂纹前缘可用曲线来描述，为充分表征其裂纹扩展规律，在网格划分阶段适当控制裂纹前缘结点个数，通过各个结点的扩展规律来控制新的裂纹前缘的扩展形态与轨迹。在确定各结点扩展方向之后，结合其扩展增量，可得出扩展后的位置，为了使新的裂纹前缘更加规范，通过三次样条曲线来拟合构建新的裂纹前缘的几何形状，如图2所示。

图2 裂纹前缘扩展示意图

得到新的裂纹前缘后，将原有裂纹模型删除，根据新的裂纹前缘建立新的裂纹体。利用ANSYS软件APDL语言对裂纹体与非裂纹体进行参数化建模，然后对新的模型进行加载求解得到下一步扩展后的裂纹前缘结点，利用三次样条曲线拟合得到新的裂纹前缘。对上述步骤循环多次后，通过三次样条曲线在每一步扩展过程中拟合得出的裂纹前缘形状，即为对应裂纹的扩展形态，而裂纹扩展过程中的路径即为裂纹扩展轨迹。

本研究根据以上数值模拟的思想，使用数学方法并结合ANSYS参数化语言(APDL语言)编制了相应的子程序，实现了基于ANSYS软件的三维裂纹扩展轨迹研究仿真系统。

2 三维穿透裂纹扩展模拟

2.1 三维薄板穿透裂纹扩展模拟

2.1.1模型几何参数

首先分析含穿透裂纹的三维薄板结构，在拉伸载荷作用下的裂纹扩展，结构如图3所示。模型几何参数为：长80 mm，宽40 mm，厚度20 mm，含穿透边裂纹，裂纹初始长度a=6 mm，受轴向载荷σ=100 MPa。模型材料为2024-T62 铝合金，材料参数为：弹性模量E=71 000 MPa，泊松比ν=0.33。

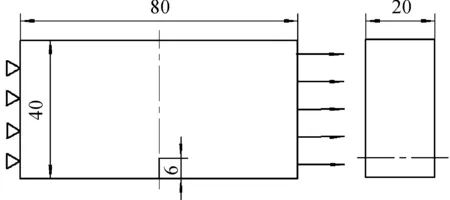
图3 穿透边裂纹受单向拉伸模型

2.1.2有限元模型

为了体现裂纹尖端奇异性，在模拟裂纹尖端应力应变场时采用奇异单元，对于三维结构，在裂纹尖端前缘采用三维20结点六面体单元的楔形退化形式，单元类型如图4所示，对于其他部位采用二次四面体单元。

图4 20结点单元及退化楔形单元

为了兼顾计算的速度与精确度，将有限元模型分为非裂纹体模型和裂纹体模型以便划分不同类型的网格[15]，此模型的几何形状独立性还表现在被镶嵌体自由表面不局限于平面，可以实现任意形状的裂纹扩展，增强程序的通用性。图5为含裂结构几何构造过程示意图。

图5 含裂结构几何构造过程示意图

对于三维裂纹结构，由于三维裂纹的前缘往往是较为复杂的形状，ANSYS软件中并没有提供类似于二维裂纹那样的方法来直接建立裂纹尖端局部网格，ANSYS的命令流也无法直接进行裂纹模拟，可以通过先对裂纹体的表面使用KSCON命令进行二维裂纹模拟，然后通过扫略VSWEEP方式来生成整个裂纹体的三维网格同时删除表面的二维网格。裂纹前缘单元为20结点等参元(SOLID186)的楔形退化形式，如图6所示。裂纹体有限元网格模型如图7所示。

图6 裂纹前缘楔形网格

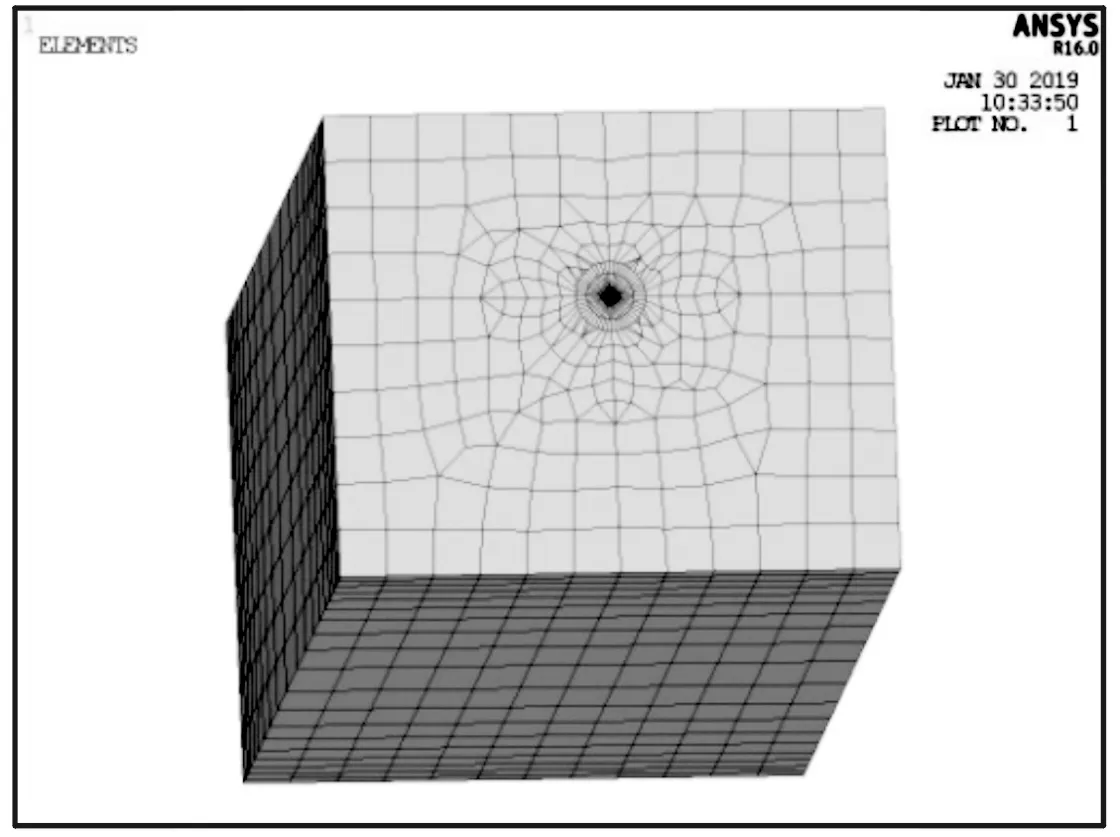
图7 裂纹体有限元网格模型

再对模型的非裂纹体部分进行有限元网格划分。为了提高计算速度，其他部分的网格单元密度较小，选用二次四面体单元自由划分。整体模型的有限元网格如图8。

图8 整体模型有限元网格

完成上述的建模后对结构进行加载和分析，由ANSYS后处理功能可得到结构的应力分布，如图9和图10所示。

2.1.3裂纹前缘应力强度因子

本算例中的三维裂纹受到自由表面和厚度效应的影响，靠近自由表面两端处于平面应力状态，中间部位处于平面应变状态。在初始裂纹前缘网格划分过程中，裂纹前缘布置20个结点，两边较密，中间较疏，如图11所示。由于ANSYS计算应力强度因子是要求X轴与裂纹面平行，Y轴与裂纹面垂直，故在裂纹尖端位置建立局部坐标系，生成的局部坐标系如图12所示。

图9 结构应力云图

图10 裂纹前缘应力云图

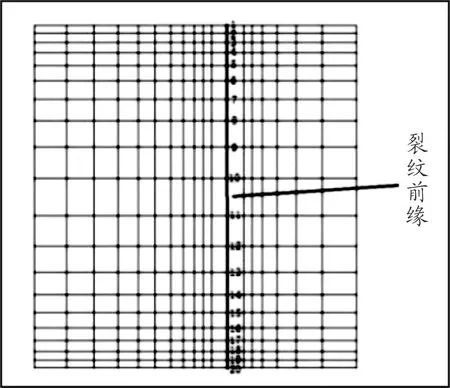
图11 裂纹前缘结点分布示意图

图12 裂纹尖端局部坐标

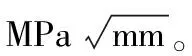
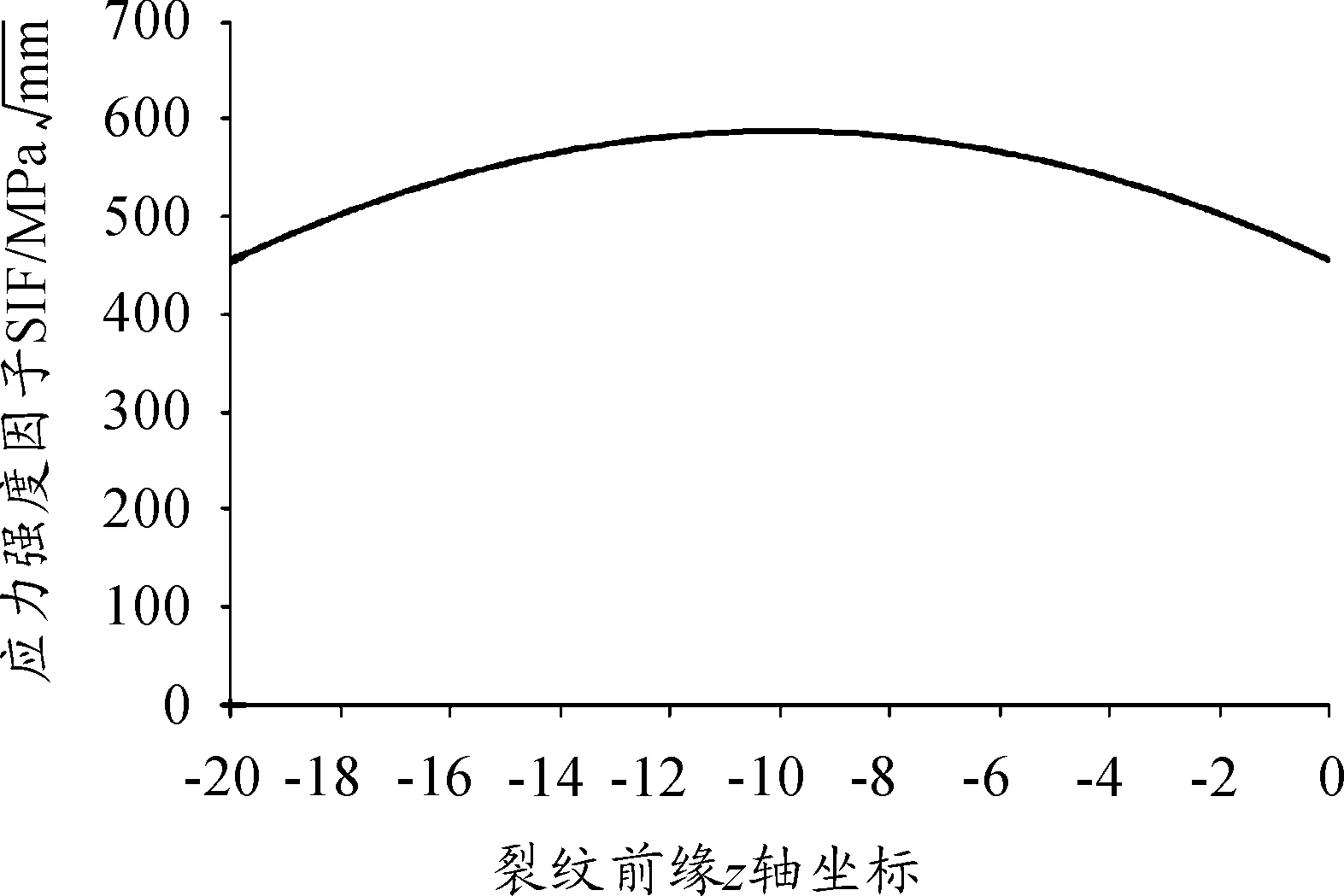
图13 裂纹前缘各结点应力强度因子分布

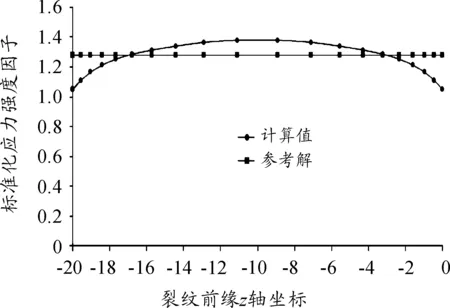
图14 裂纹前缘标准化应力强度因子计算值与理论解[16]曲线

从图14可以看出，考虑厚度效应时，裂纹前缘接近自由表面的点处的应力强度因子值小于理论解，中间点处的应力强度因子值大于理论解。因此在进行裂纹扩展分析过程中，不能忽略裂纹前缘的厚度效应。

对该模型进行了6次裂纹扩展模拟，图15给出了每次扩展时裂纹前缘结点沿厚度方向(即为Z轴方向)的应力强度因子分布规律(其中crack代表初始裂纹前缘应力强度因子，crack1-crack6分别代表扩展1次到扩展6次的裂纹前缘应力强度因子)。

图15 裂纹前缘各结点的应力强度因子曲线

从图15可以看出，前4次扩展裂纹前缘各结点的应力强度因子分布与裂纹初始状态时的应力强度因子分布相似，而后2次扩展时裂纹前缘应力强度因子分布“杂乱无章”，反映了裂纹扩展过程中应力场的变化，即：即：三维薄板穿透裂纹在单向拉伸载荷作用下，裂纹沿初始裂纹面扩展，靠近自由表面两端处于平面应力状态，中间部位处于平面应变状态，即位于中间部位的裂纹应力强度因子比靠近自由表面的应力强度因子大，但扩展到后期时沿裂纹前缘的应力强度因子并不完全遵循这样的变化规律，由于厚度效应的影响，应力强度因子分布成为随机排布。

2.1.4裂纹扩展形态与轨迹分析

在计算裂纹扩展时，假设裂纹前缘各结点之中应力强度因子最大值所对应的结点的扩展增量Δai=1 mm，则其余各结点的扩展增量可由式(2)依次得出，计算出各个结点扩展量之后，利用三次样条曲线拟合出新的裂纹前缘(即裂纹扩展形态)，之后更新有限元模型，进行裂纹扩展分析。图16给出了6次扩展时的裂纹形态(其中crack代表初始裂纹前缘形态，crack1-crack6分别代表扩展1次到扩展6次的裂纹前缘形态，Z轴为厚度方向，Y轴为裂纹扩展方向)。可以看出沿厚度方向，两边扩展较慢，中间扩展较快，裂纹前缘在扩展多次后呈现隧道型。

图16 裂纹前缘形态

2.2 三维大厚度板穿透裂纹扩展模拟

2.2.1模型几何参数

图17给出的是含穿透裂纹的大厚度板三维结构。模型参数为：长80 mm，宽40 mm，厚度60 mm，含穿透边裂纹，初始裂纹长度a=6 mm，受轴向载荷σ=100 MPa。模型材料为2024-T62 铝合金，材料参数为：弹性模量E=71 000 MPa，泊松比ν=0.33。

图17 含穿透边裂纹的三维大厚度板

2.2.2有限元模型

网格划分时裂纹尖端前缘仍然采用三维20结点六面体单元的楔形退化形式(SOLID186)(如图4所示)。有限元建模[17]仍然分为两部分：非裂纹体和裂纹体进行建模，裂纹体有限元模型如图18所示。

图18 裂纹体有限元模型

2.2.3裂纹扩展形态与轨迹

分析流程与薄板结构裂纹扩展分析流程相同，利用本文建立的三维裂纹扩展轨迹仿真系统，对该模型进行裂纹扩展分析。图19给出了经过5次扩展的裂纹前缘形态(其中crack代表初始裂纹前缘形态，crack1-crack5分别代表扩展1次到扩展5次的裂纹前缘形态，Z轴为厚度方向，Y轴为裂纹扩展方向)。从图19可以看出，随着裂纹扩展的发展，裂纹前缘呈现出双隧道型，说明对于大厚度结构裂纹前缘应力状态更加复杂。对于三维大厚度板穿透裂纹在拉伸载荷作用下，内部呈现出复杂的应力应变状态，可近似认为靠近自由表面两端与中间部位处于平面应力状态，而中间与两端之间的部分处于平面应力状态，即中间与两端的应力强度因子小于内部的应力强度因子，故中间与两端的裂纹前缘扩展较快，因此裂纹前缘会呈现 “双隧道型”。

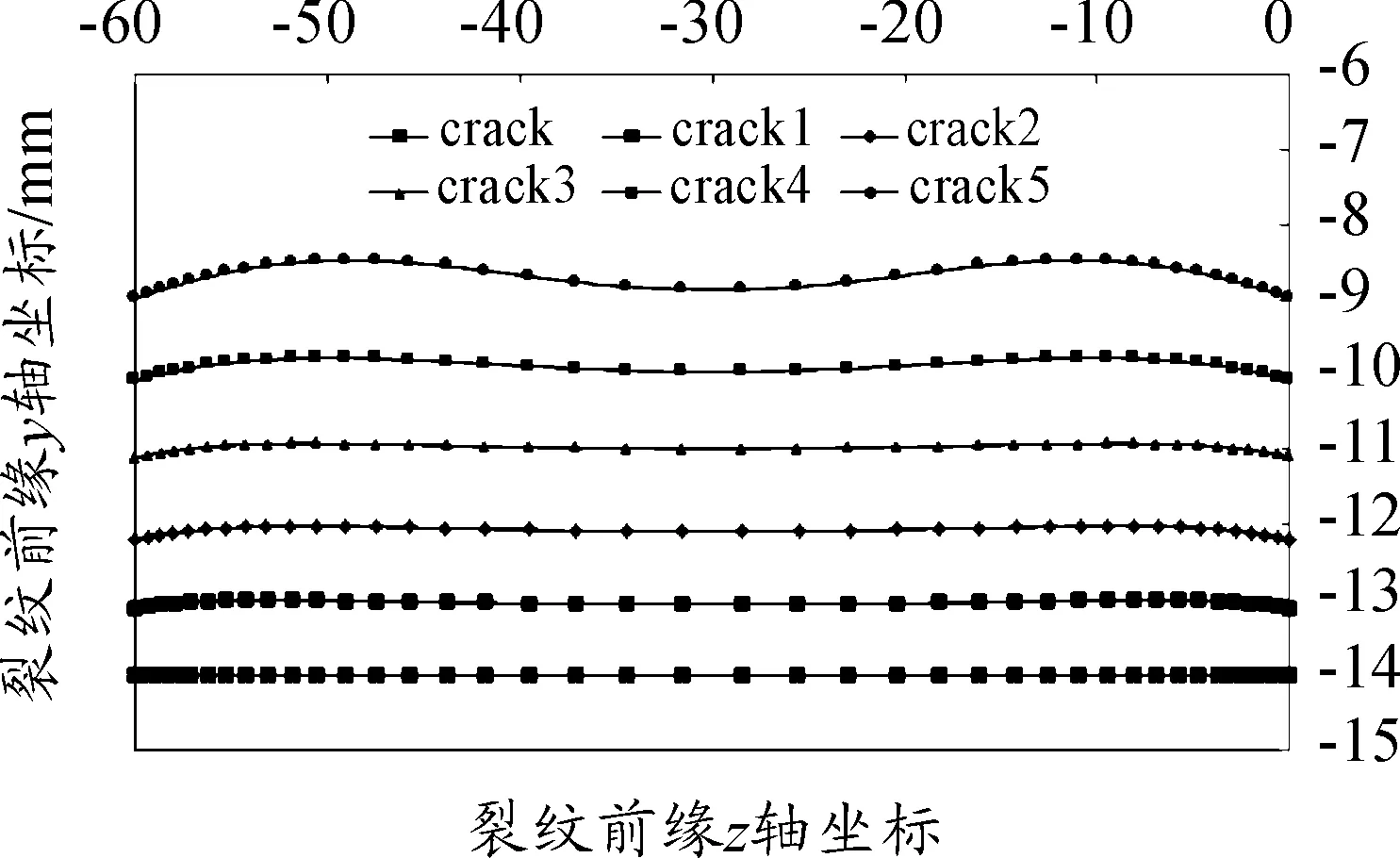
图19 裂纹前缘形态

3 验证

三维穿透裂纹在扩展过程中表现为“隧道效应”的特征[18-19]，即对于包含有初始直线裂纹前缘的穿透裂纹试样，随着试样经受循环加载，中心处裂纹扩展速率大于靠近自由表面两端处裂纹，形成隧道形状的裂纹前缘形貌，称之为“隧道效应”。

在文献[20]中开展的厚度分别为20 mm、60 mm的7050-T7451铝合金单侧裂纹板(L-T方向)拉伸疲劳裂纹扩展试验中也发现，随着试样厚度的增加，裂纹前缘形貌发生改变，“隧道效应”减弱。一般当试样厚度增大到大于试样的宽度时，甚至会出现了“双隧道效应”(或称“马鞍效应”)，裂纹前缘形貌呈“马鞍型”。试验载荷及环境工况见表1，疲劳载荷为常幅载荷，正弦波形，应力比为0.06。两组试样断口宏观形貌如图20和图21所示，其中图20为厚20 mm试样的断口形貌，图21为厚60 mm试样的断口形貌。

表1 不同厚度板单侧裂纹扩展试验载荷及环境条件

图20 厚20 mm试样的断口形貌

图21 厚60 mm试样的断口形貌

对比仿真模拟结果与文献[20]试验结果，可以看出裂纹前缘仿真结果与试验结果吻合较好，说明本文仿真方法可行。

4 结论

1) 基于ANSYS软件建立了三维裂纹扩展轨迹仿真系统。利用该系统模拟了拉伸载荷作用下三维穿透裂纹的扩展轨迹，研究了裂纹前缘应力强度因子的分布规律，揭示出裂纹扩展规律，并与试验结果进行了对比，证明了本文建立的仿真系统的可靠性和准确性。

2) 三维薄板穿透边裂纹在单向拉伸载荷作用下，中间的应力强度因子大于两端，但扩展到一定阶段后沿裂纹前缘的应力强度因子变得“杂乱无章”。裂纹沿初始裂纹面扩展，内部可认为是平面应变状态，且中间裂纹的扩展速度比两边裂纹的扩展速度要快，裂纹前缘形态呈“隧道型”。

3) 三维大厚度板穿透边裂纹在拉伸载荷作用下，内部呈现出复杂的应力应变状态，不能简单地认为是平面应变状态。裂纹前缘会呈现出“马鞍型”，即为“双隧道型”。

4) 本文数值仿真结果与文献[20]试验结果证明对于不同厚度的三维裂纹，内部的应力应变场相差很大，裂纹前缘也呈现出完全不同的形态。