优化提问策略，提升课堂效率*

☉江苏省泰州市姜堰区实验初级中学 黄 静

“课堂提问”是一门具有深奥性和哲理性的教学艺术.在课堂教学中，教师以“提问”为教学手段，复习旧知、引入新课，引导学生在探究中获取数学思想方法，习得数学经验和智慧.不过，如何提问才是最有效的，才能真正造就高效的品质课堂呢？本文中，笔者结合自身的教学实践，就如何优化提问策略，提升课堂效率，谈谈自身的几点思考.

一、以提问为指向创设问题情境，激发学生的学习欲望

教学方法的有效性在于能否触碰学生的情感领域，能否磨炼学生的意志品质，能否深入学生的内心需求.在课堂教学中，教师需创设合理的问题情境，借助情境的导入，指明教学的方向，凸显教学主要内容，激发学生的学习欲望，引领学生的探究激情.

例如，笔者在教学“相交线中的角”这一内容的过程中，以已学知识“两条直线相交所构成的角”导入，借助旧知的回顾，自然引入新课的学习.以问题为载体，以实践活动为主线，引导学生在“三线八角”的探究中渐入课堂，点明主题.具体教学过程如下：

1.回顾引新，创设情境

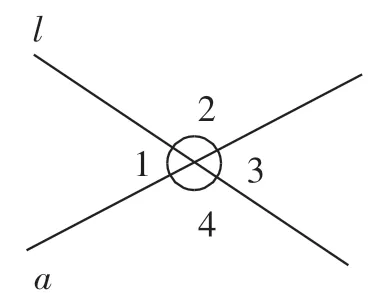
图1

例1 如图1所示，已知直线a和直线l相交，并得4个角：∠1、∠2、∠3、∠4.仔细观察这4个角的位置特征及数量关系，得出其中对顶角有（ ），邻补角有（ ）.

2.积极思考，实践探究

引导学生在两条直线相交的平面内，再画出一条直线b，使之与直线l相交，并请学生思考：“可以画出多少种不同情形的直线？此时图形中所增设的不同位置的角你能否全部厘清？”

由于新问题的添置，一些角的关系再无法用已学知识进行表述.这样一来，一方面贴近学生的认知需求，迎合了学生的探究兴趣，激发了他们的学习欲望；另一方面，点明了本课学习的主题，为新课学习奠定了坚实的基础.

二、课堂提问须因“才”施“问”，树立学生的自信心

在课堂教学中，教师对问题的设置既需具有针对性，又需具有一定的难度.教师需牢牢把握难度，以学生通过努力思考可以解决的难度为最佳.因此，教师课前需做足功课，分析学生的知识缺失点和困难点，并针对不同层次的学生，提出不同的问题，使每个学生都可以收获成功的快乐，并在各自的水平上有所提升，有所发展.

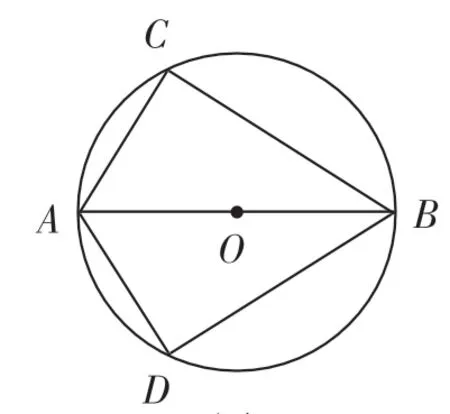
图2

例2如图2所示，已知圆O的直径为AB，并有AC=AD.

笔者提出分层问题，如下：

（1）请求出∠C、∠D的度数.

（2）你认为△ABC和△ABD全等吗？请说出理由.

（3）请尝试用多种方法证明△ABC和△ABD是全等三角形.

此例题层层递进，大部分学生都能很快完成问题（1）和（2），一小部分学优生可以完成问题（3）.这种将问题的难度分拆、分散的教学策略，使不同层次的学生在各自的水平上都能得到锻炼，取得进步.分层后，知识呈现螺旋上升的原则，每个学生都能选择适合自己的问题，充分调动学生学习的积极性，让学生主动、积极、乐学，进而实现所有学生在各自不同基础上的共同进步，从而提升教学质量.

三、课堂提问设置一定的悬念，吸引学生的注意力

在课堂教学中，教师设置具有一定悬念、别出心裁的问题，可以充分吸引学生的注意力，激发学生进一步探究的欲望.课堂伊始，教师可以从具体实际出发，通过制造问题中的“悬疑点”，积极引导学生进行思考，进而及时捕捉问题中的“兴趣点”，激发学生的好奇心，启迪学生的思维.

例如，笔者在教学“直角三角形”这一内容的过程中，创设了以下问题情境：该如何去测量山峰、树木、铁塔的高度及琥珀的宽度呢？在实际问题情境中，让学生基于理性，点燃思维之火，自主发现数学的应用性，感悟数学知识的价值性，从而激发浓厚的学习兴趣.

再如，笔者在阐述“三角形内角和定理”和“中位线定理”之前，以以下问题组来吸引学生的注意力：

（1）工厂里的一块三角形形状的有机玻璃板不知何故残缺了一角，工人希望以此作为模型复制一块一样的玻璃板，你能替他想想办法吗？

（2）横在牛郎村和织女村之间的那个湖泊，让牛郎和织女焦头烂额，相见十分困难，你能想出办法替他们测一测两村之间的距离吗？

（3）以上两个问题你们感兴趣吗？想替他们解决这个难题吗？

笔者以“问题组”的形式制造悬念，引导学生进入新课学习，通过问题（1）引入“三角形内角和定理”，通过问题（2）引入“三角形中位线定理”.通过两个与现实相关联的、有趣的、有创意的问题，让学生倍感兴趣，愿意去学，主动思考，充满惊喜，有利于学生数学意识的培养，在深入的理解中，完善知识，发展思维，从而提升课堂效果.

四、课堂提问留有探究空间，拓展学生的创造性思维

每个学生的心灵深处都渴望自己是一个发现者、一个思考者、一个研究者、一个探究者.在提问时，教师需营造轻松、和谐的氛围，给足学生思考、探究的时间和空间.很多时候，一些教师在问题提出后，由于担心学生思维的偏差，未等学生充分思考便匆匆诱导、提示，将解决问题的关键点告知学生.当然，这样一来教学的进程顺畅了，探究的时间缩短了，不过学生缺失了探究知识发生和发展的进程，无法实现学生思维的自然生长，不利于独立思考能力的培养.

例3计算：

在探究此题时，教师可以让学生用自己的方法尝试.当然，在计算时肯定会出现极其烦琐的方法和过程.教师在学生解题后，可以请有不同解题思路的学生讲一讲解题方法，让学生在观察、比较和分析中，找出最优解法.从探究的过程来看，学生收获的不仅仅是一个解题方法，还在探究中生成了学力，牢固掌握了知识，提升了学生的数学素养.

五、课堂提问需活灵活“变”，提高学生的数学能力

问题的变式是将其本质保留下来，灵活地变通非本质部分，从不同的思维角度或问题情境中训练学生的思维.这种变式训练可以深化和活化学生的思维.

例4如图4所示，点C位于线段BD上，且△ABD与△CDE都为等边三角形，求证：AD=BE.

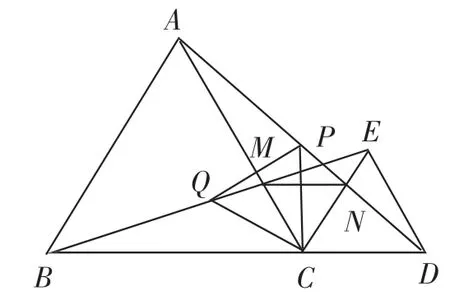
图4

变式问题1：线段MC和线段NC是否相等？请求证.

变式问题2：线段MN和线段BD是否平行？请求证.

变式问题3：若∠BAD=90°，线段BE和线段ED是否垂直？请求证.

变式问题4：如果点P是线段AD的中点，点Q是线段BE的中点，那么△CPQ是什么三角形？

事实上以上问题，通过相同题干和图形，为学生节约了读题、审题和画图的时间.因此，教师可以通过增减和变化条件、延伸结论或条件、互换条件和结论、一题多解等方法，创设新题型，开阔学生的思路，发散学生的思维，培养学生的思维能力和探究能力，从而达到提升课堂效率的效果.

总之，在课堂中，教师需有效对学生进行提问，提升课堂教学的质量，提高学生的综合素养.因此，初中数学教师遵循学生的主体地位，充分发掘学生的潜能，创设高质量的问题，增强课堂教学的实效性，为学生的发展奠定坚实基础.