学生“一题多错”的诊评与教学跟进——从一个学生的3次订正说起

☉江苏省海安市海陵中学 刘 生

教学即研究，某天在课堂上安排一个班级“中位数”水平的女学生上台讲一道习题，结果她连续3次都出错，笔者课后针对她的这3次错误进行了教学思考，课后再次找这个学生进行了有针对性的辅导，取得了较好的教学效果.本文就从这个学生的3次订正说起，并提出一些教学建议，供研讨.

一、从学生的3次订正说起

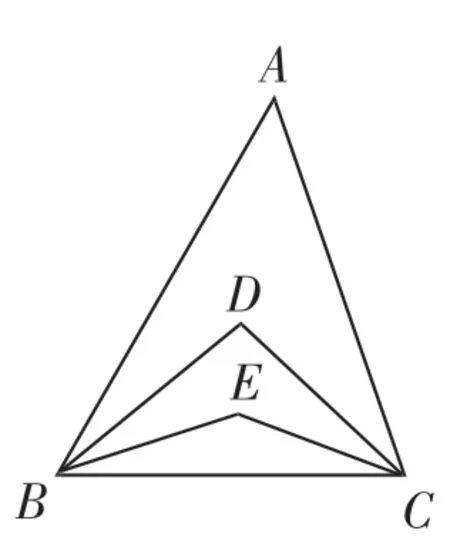
图1

习题：（某单元测试卷第18题）如图1，在△ABC中，∠A=42°，∠B和∠C的三等分线分别交于点D、E，则∠BDC等于___________.

教学记录：考虑到这道习题前期教学过程中已遇到多次，就安排了一名班级“中位数”水平的女学生上台讲解思路.

第1次错误，她直接写出一个错误答案84°，我追问：“你怎么这么快就得到了答案？”她赶快说“好像错了”，然后说错记成一个什么“两倍角”的基本图形.接着她开始订正，出现第2次错误，想当然认为∠ABC、∠ACB是相等的，进而默认∠ABD=∠DBE=∠EBC=∠ACD=∠DCE=∠ECB，过程再次出错.第3次订正时，她的思路贯通了，将“∠DBC=∠DCB”视为整体处理，但列算式时，没有用规范的推理语句，运算又出错.

简评：分析这名学生的几次错误.第1次错误，属于基本图形掌握不扎实，随意套用模型，说明该生读题、审题不清，误认为是“两倍角的基本图形”“∠ABC=∠ACB”，现在很多学生都存在读题粗糙的现象，要解决，首先要让学生认识到自己的问题，再从动嘴、动手、动脑三方面解决.

第2次错误，属于审题不清，这是很多学生解这道题时存在的问题，似乎认为∠ABC和∠ACB相等这样的特殊情况可以代替一般情形，实则不然，提醒学生要学会“正确联想”.解题时会联想，这是这名学生值得表扬的地方，但要根据实际题目去联想，而不是凭借头脑中的“固有经验”胡思乱想，如“两倍角”的基本图形的解题方法可以应用于“三倍角”的图形，但不能直接误认为是“两倍角”的基本图形.

第3次错误，对几何语言的规范性掌握不好，没有进行规范的书写和几何推理，按步骤去计算，忽略这里面的“整体”思想，造成过程混乱.这提醒我们，在几何教学中，要重视数学语言表达能力和运算能力的培养.这是一名中等生，她身上暴露出来的问题相信也是学生中普遍存在的问题，即数学语言表达能力和运算能力欠缺，课上、课后要让学生多说、多练，尤其是七年级的学生，刚刚接触几何，逻辑思维能力和数学表达能力都在培养阶段，还有很大的提升空间.

二、对该类学生的教学跟进

为了更好地做好教学应对，我们针对这类学生的“典型症状”，给出如下的解题教学微设计.

例1如图2，在△ABC中，∠A=42°，∠B和∠C的平分线交于点E，则∠BEC等于______.

设计意图：回忆基本图形，要求学生写出具体的推导过程，建立∠BEC与∠A的关系.

变式1：如图3，在△ABC中，∠A=42°，∠B和∠C的三等分线分别交于点D、E，则∠BEC等于______.

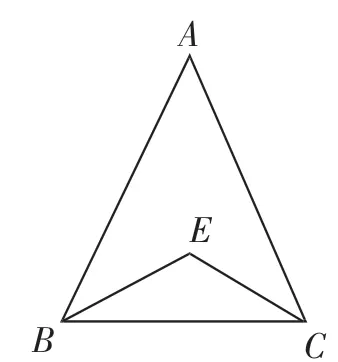
图2

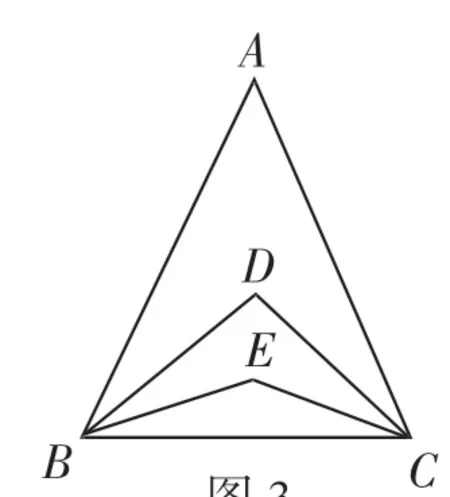
图3

练习1：如图3，在△ABC中，，则∠BEC等于______.（用含n的式子表示）

设计意图：从角平分线、三等分线中抽象出模型，检验学生对整体思想的把握.

变式2：回归原题，略.

教学思路：从上述练习中，学生迁移运用，表示出，整体求解.部分学生联想到我们学过的另一个基本图形，即“飞镖型”，

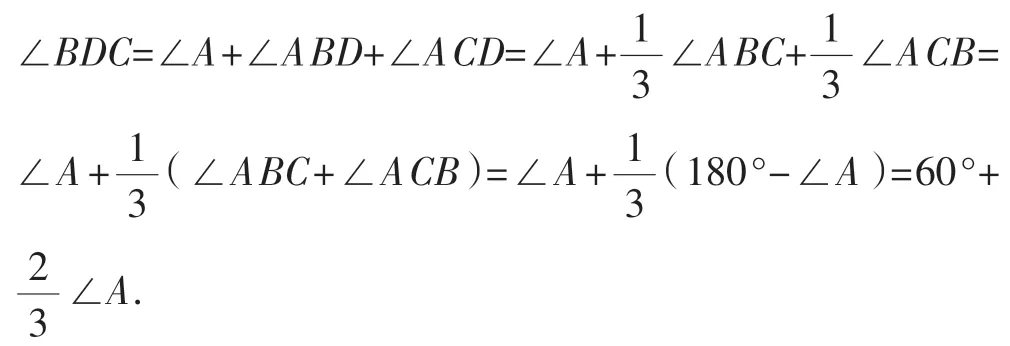
拓展：感兴趣的同学还可以总结一般规律：n等分线的第一个夹角∠A，n等分线的最后一个夹角=

最后，给出一些同类习题，变式再练，巩固所学.

题1：如图4，在△ABC中，∠BAC=56°，∠ABC=74°，BP、CP分别平分∠ABC和∠ACB，则∠BPC=___________.

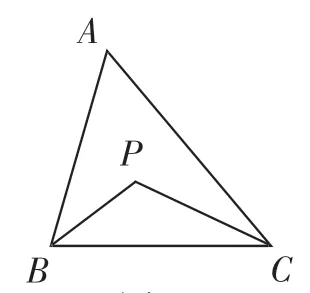
图4

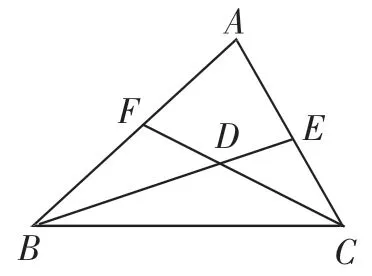
图5

题2：如图5，BE、CF都是△ABC的平分线，且∠BDC=110°，则∠A的度数为___________.

题3：如图6，在△ABC中，∠ABC的平分线BD与∠ACB的外角平分线CD交于点D，如果∠ABD=20°，∠ACD=55°，那么∠A+∠D=___________.

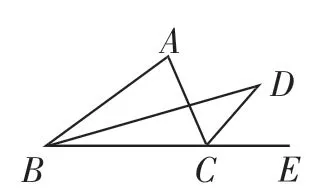
图6

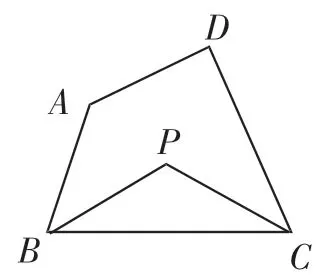
图7

题4：如图7，在四边形ABCD中，∠A+∠D=α，若∠ABC的平分线与∠BCD的平分线交于点P，则∠P=___________.

三、进一步的思考

这名学生的3种错误与她所处的“班级位置”基本上是对应的，比如，对基本图形及性质有印象，但是记错、记串模型（与记忆力有关？），再比如，对这些基本图形互相混淆与简单记忆是否有关？教学上该如何避免简单记忆基本图形及性质而印象模糊？这些都值得深入思考.以下再围绕几何解题教学给出一些思考和建议.

1.要根据习题难度选择相关学生展示

在目前的课改背景下，课堂教学中注意开展对话追问是很多教师的自觉追求，然而我们在一些课堂观察中发现，教师与少数优秀学生之间的单向对话比较常见，而让一些学有困难的学生参与课堂对话的机会并不多.因为这类学生“反应慢节奏”，如果安排他们进行课堂展示或开展对话，常常会消耗宝贵的课堂时间，所回答的问题也得不到完满的解答，影响了教师的课堂教学进程，不利于整体学程的推进，所以这类学生在课堂上往往得不到更多的对话机会，常常成为“听众”.这方面一个较好的应对策略是，通过精心预设的不同难度的问题选择不同类型的学生参与回答和展示，教师要预设好可能的一些问题，并做好预案，跟进追问，引导优秀学生参与评析，让更多学生的思维被卷入到对话追问、反思评析的学程中来，这样就达到了较好的“走向共生”的课堂教学效果.

2.要认真开展基本图形及性质的教学研讨

从上面的案例可看出，让一些学有困难的学生试着多花时间去推导一些基本图形及性质，拉长思考过程，是有效的做法.可以让该生课后对三角形“双角平分线”的夹角问题进行全面推导、梳理，最好能写成数学小论文一样的文章，以便加深对这类基本图形及性质的理解，训练精准识别的“眼力”.事实上，从应试训练、精准备考的角度看，认真开展基本图形及性质、很多“二级结论”（教材上没有升级为定理、性质、推论）的教学是非常有必要的，但不能只是“一个性质、口诀记忆、大量练习”的教学取向，而应该引导学生从简单的公理、定理出发，逐次呈现、演算推理得到新的结论，让学生对这类新结论的演算推理过程有较好的理解，一方面，可以积累这些结论，另一方面，在这个过程中也训练了更基础的定义、定理，体现了“回到定义或概念去解题”的解题思想.

四、写在后面

上面从我们每天“所见所闻”的学情素材出发，通过本文案例及解读说明我们需要修炼教师的专业基本功——“诊评和治疗”.当然，这也正是教学评价与因材施教的基本要求.最后，期待更多的“教学手边素材”及研讨的案例分享和解读，让我们能够师生教学相长、互相学习、分享教学智慧.