在数学教学中渗透数学思想

☉江苏省苏州市吴中区碧波中学 朱方政

数学思想是数学知识的重要组成部分，是数学的灵魂，是数学的精髓.初中数学知识中蕴含很多数学思想，如转化思想、数形结合思想、分类讨论思想、类比思想、方程思想、整体思想、估算思想等.教材中虽然没有明确提出这些数学思想，但通过每章小结等形式向学生渗透这些数学思想.数学思想不同于数学知识，它来源于数学知识而又高于数学知识，常常渗透在数学知识之中，是指导我们解决数学问题的根本策略.在教学时，要注意有意识地向学生渗透数学思想.那么，应该怎样向学生渗透数学思想呢？下面结合自身教学实践，从三个方面说明.

一、在课堂引入时渗透数学思想

初中数学中的每个章节都渗透有数学思想.不过有的章节渗透的数学思想比较明显，有的则比较隐含.对于那些明显渗透数学思想的教学内容，可以在引入时渗透数学思想.比如，在教学分式的基本性质时，在引入时可以先设计下面的问题：

题1：把下面的分数化为最简分数：

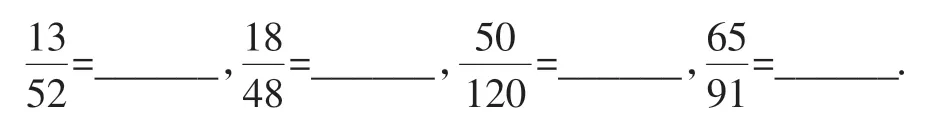
题2：填空：

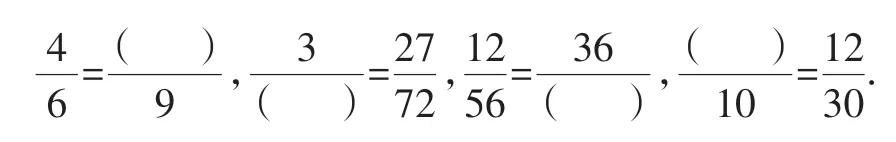
题3：判断下面的算式是否正确：

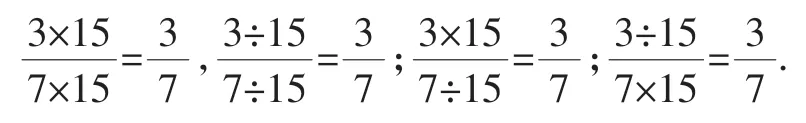
题4：把和化成分母是10而大小不变的分数，则

题5：对于任意一个分数，当c≠0时，可以猜想（填“=”或“≠”）.

题6：分数的基本性质：分数的分子和分母同时乘或者除以相同的数（ ），分数的大小（ ）.类比分数的基本性质，可以猜想分式的基本性质为：___________，用式子可以表示为___________.

通过这样的引入，很自然地向学生渗透了一种数学思想：类比思想.将分式与分数进行类比，从分数的基本性质自然过渡到分式的基本性质，过渡非常自然，学生易于接受分式的基本性质，同时便于学生切实感悟类比思想.

二、在复习小结中渗透数学思想

在章节小结、复习的数学教学中，由于涉及的知识点较多，知识容量较大，蕴含的数学思想也较多，在教学时要尽可能把那些比较典型的数学思想有意识地向学生渗透，帮助学生掌握章节知识，厘清知识之间的关系.

例如，在复习“平行四边形”一章时，四边形之间的关系如图1所示：

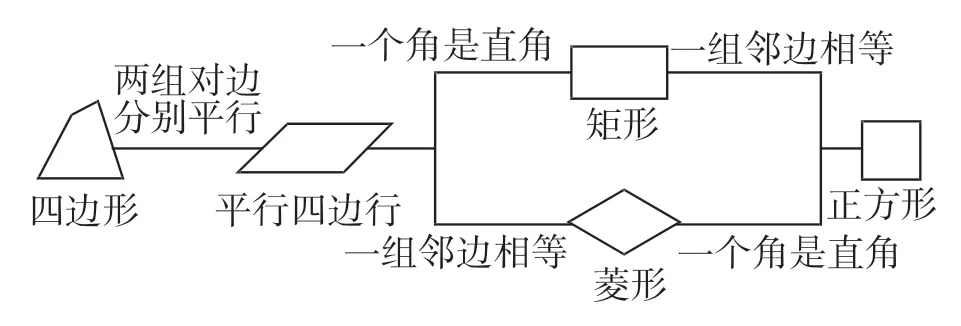
图1

可以向学生提出这些问题：

问题1：如何判定一个四边形是平行四边形？（①两组对边分别平行；②两组对边分别相等；③一组对边平行且相等；④两组对角分别相等，满足①②③④中的任意一个选项，这样的四边形就是平行四边形，向学生渗透从一般到特殊的思想）

问题2：特殊平行四边形包括哪些四边形？（矩形、菱形和正方形，向学生渗透分类思想）

问题3：证明一个四边形是菱形时，可以先证这个四边形是平行四边形，然后证明这个四边形有一组邻边相等或对角线互相垂直或对角线平分一组对角；证明一个四边形是矩形时，可以先证这个四边形是平行四边形，然后证明这个四边形有一个角是直角或对角线相等，向学生渗透转化思想.

问题4：正方形既是矩形又是菱形，兼具矩形和菱形的性质，在证明一个四边形是正方形时，可以先证明这个四边形是矩形，然后证明这个矩形有一组邻边相等或对角线互相垂直或对角线平分一组对角，也就是证明这个矩形是菱形；也可以先证明这个四边形是菱形，然后证明这个菱形有一个角是直角或对角线相等，也就是证明这个菱形是矩形，向学生渗透转化思想.

通过提出这些问题，向学生渗透分类思想、转化思想、从一般到特殊的思想等，同时有利于厘清平行四边形、矩形、菱形和正方形之间的关系.

三、在解题教学中渗透数学思想

在教学中向学生渗透数学思想，一个最重要的目的是让学生在数学思想的指导下，能够利用这些数学思想帮助他们分析和解决问题，毕竟数学思想有“指路明灯”的作用.为此，在解题教学中，我们应该有意识地设计一些与渗透的思想有关的数学问题，让学生“现学现用”“活学活用”.

初中阶段我们学习了函数，而函数图像是数形结合的重要工具，利用函数图像解决问题是数形结合思想的重要体现.学习了一次函数的知识后，我们知道二元一次方程组的解可以看作二元一次方程组中的两个方程对应的两个一次函数图像的交点的坐标，教材中涉及一次函数的内容有对应的例题，在讲完该例题后，为了进一步向学生渗透数形结合的思想，我“趁热打铁”，给学生布置了如下一道练习题：

如图2，在长方形ABCD中，点E是线段AB靠近点A的一个四等分点，AB=4，BC=8，连接DE，交对角线AC于点M.求△AEM的面积.

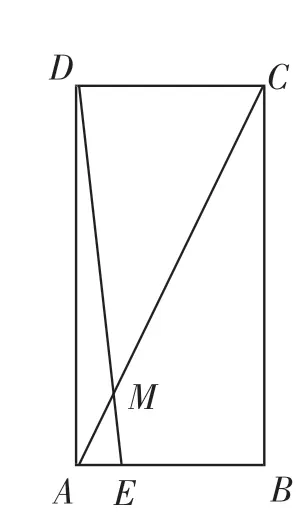
图2

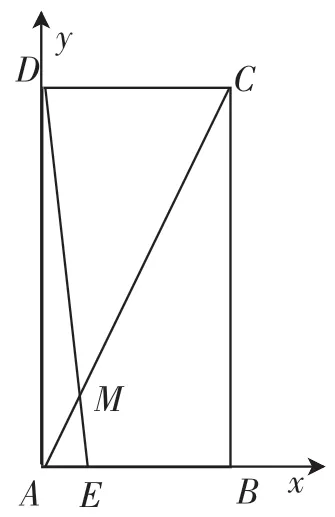
图3

要求△AEM的面积，根据已知条件，只需求出AE边上的高就行了，如果学习了相似三角形的知识，求AE边上的高就是“小菜一碟”，但相似三角形属于九年级的知识，因此该题对于还未学习相似知识的八年级学生来说，肯定具有一定的挑战性，当然这也正是我设计此题的动机所在——向学生渗透数形结合思想，让学生利用函数知识解答此题.经过思考，还真有不少学生解出了该题.他们以点A为原点，AB所在直线为x轴，AD所在直线为y轴，建立了如图3所示的平面直角坐标系.这样可以立即得到A、B、C、D四点的坐标，利用待定系数法求出直线AC的解析式y=2x，直线DE的解析式y=-8x+8.联立两直线的解析式，便可求出点M的坐标，也就可以得到△AEM的边AE上的高，也就可以求出△AEM的面积.这些学生能够想到利用函数图像解答，说明他们对数形结合思想有一定的感悟和理解，同时达到了向学生渗透数形结合思想的目的.

再如，转化思想是解决三元一次方程组问题的主要思想（化三元为二元，化二元为一元）.学习了三元一次方程组的知识后，为了向学生渗透转化思想，我有意布置了如下一个实际问题：某水上公园有大、中、小三种型号的游船.5艘大型游船、3艘中型游船、1艘小型游船一次最多可以载乘客152人；7艘大型游船、4艘中型游船、1艘小型游船一次最多可以载乘客207人.你能算出1艘大型游船、1艘中型游船、1艘小型游船一次最多可以载乘客多少人吗？

解答此题首先应设1艘大型游船、1艘中型游船、1艘小型游船一次最多可以载乘客的人数分别为x、y、z，根据题意列方程组，得接下来就是要求出x+y+z的值.由于只有两个方程却有三个未知数，显然无法求出每个未知数的具体值，一些学生分析至此思维会受阻.由于我在讲解三元一次方程组知识时经常向学生渗透转化思想，因而有不少学生想到将原方程组转化为三元一次方程组，如视z（x或y）为常数，原方程组可以转化为这样x、y都用含z的字母表示，可以顺利求出x+y+z的值.

作为数学教师，向学生传授数学知识固然重要，在教学过程中适时向学生渗透数学思想也是非常重要的一个环节.数学知识是基础，数学思想是引导.在今后的教学中，我将更加注重对学生进行数学思想的渗透，提高学生分析问题和解决问题的能力，从而提高学生的数学素养.