由“五点共圆”问题引发的猜想

☉海南省海南中学 何佳译

☉海南省海南中学 屈 韬

2000年12月20日下午，江泽民同志视察澳门濠江中学.在与教师座谈时，江泽民同志说：“我高中毕业参加高考时的一道几何题，至今印象深刻.”随后江泽民同志拿过一张白纸画了个五角星，边画边说：“假设：任意一个星形，五个三角形，外接圆交于五点.求证：这五点共圆.”这就是著名的“五点共圆”问题.

“五点共圆“问题用书面语言可表述为：任意一个五角星，在其五个小三角形上作出五个小三角形的外接圆，两个相邻圆各自交两点，共有十个交点，除去星形本身的五个点，其余五个点必定是共圆的.目前最常见的证明方法如下：

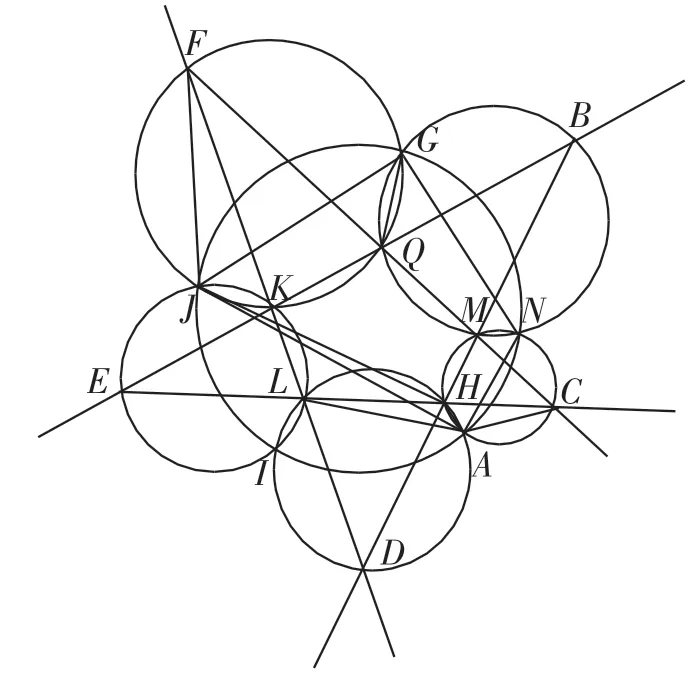
图1

证明：画任意五角星，如图1所示，△FQK、△KEL、△LDH、△HCM和△MBQ各自的外接圆顺次相交的交点分别为J、I、A、N、G.

连接CA、HA、JA、LA、NA、JH、NG、GQ、GJ、JF.

根据圆周角定理和圆内接四边形的性质定理可知：

∠FCA+∠FLA=∠AHD+∠FLA=∠ALD+∠FLA=180°.

则F、L、A、C四点共圆.

同理，F、J、L、C四点共圆，从而F、J、A、C四点共圆.

则180°-∠FJA=∠FCA=∠MCA.（注：此处的小技巧好多学生想不到）

又∠MNA=∠MCA，∠GNM=180°-∠GQM=∠GQF=∠GJF，则∠GNA=∠GNM+∠MNA=∠GJF+（180°-∠FJA）.

则∠GNA+∠GJA=∠GJF+（180°-∠FJA）+∠GJA=180°.

故J、G、N、A四点共圆.

同理可证I、G、N、A四点共圆.

则J、I、A、N、G五点共圆.

上述证明思路为：要证J、I、A、N、G五点共圆→只需证J、G、N、A四点共圆和I、G、N、A四点共圆→由于二者同理可证→只需证J、G、N、A四点共圆→通过圆周角定理和圆内接四边形的性质定理转换成证F、L、A、C四点共圆.

在上述证明过程中，直线EB上的点我们一个都没用到，如果我们去掉直线EB会是什么结果呢？去掉直线EB，我们得到图2：

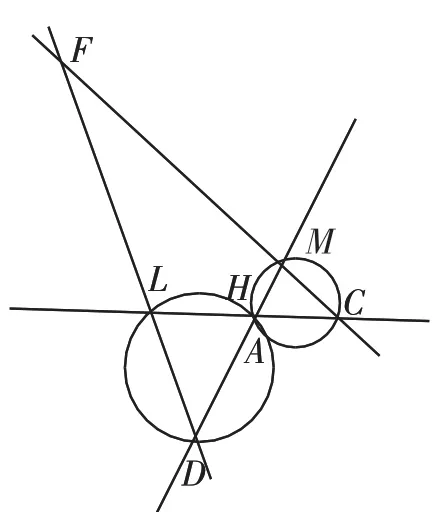
图2

图2中每三条相交直线构成一个三角形，共有△DHL、△CMH、△CFL、△DMF四个三角形，△DHL和△CMH的外接圆交于点A、H.

由“五点共圆”问题的证明可知F、L、A、C四点共圆，同理可知F、D、A、M共圆，且△DHL、△CMH、△CFL、△DMF的外接圆交于点A.因此我们可以得到图3：

图2

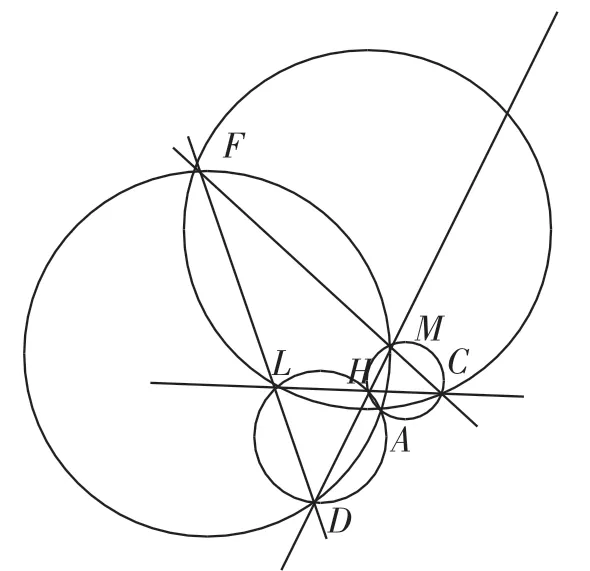
图3

在“五点共圆”问题中，五个小三角形的外接圆，两个相邻圆各自交两点，如点A和点H，共圆的为点A，而非点H.我们知道五角星是由两两相交且任意三条都不共点的五条直线相交后构成的，结合图3，可以将“五点共圆”问题简化表述为：平面内有两两相交，且任意三条直线都不共点的五条直线，其中每四条作为一组可确定一个“四圆共点”的点，共有五个这样的点，这五个点共圆.

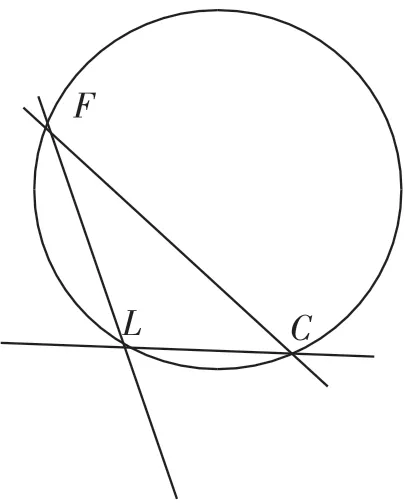
图4

如果在图3中再去掉直线DM，可得到图4：

图4中△CFL有一个外接圆，换句话说就是F、L、C三点共圆.

那么图3中的问题可以表述为：平面内有两两相交，且任意三条直线都不共点的四条直线，其中每三条为一组可以确定一个圆，共有四个这样的圆，这四个圆共点.

顺着这样的思路笔者猜想：

如果在图1的基础上再增加一条直线，得到六条两两相交且任意三条都不共点的直线，那么这六条相交直线每五条一组构成一个“五点共圆”，共有六个“五点共圆”，这六个“五点共圆”共点.

再增加一条直线的话，得到七条两两相交且任意三条都不共点的直线，那么这七条相交直线每六条一组有一个“六圆共点”的点，共有七个这样的点，这七个点共圆.

…………

推而广之，笔者猜想：

平面内有两两相交，且任意三条直线都不共点的n条直线：

当n为大于2的偶数时，n-1条直线可确定一个圆，共有n个圆，这n个圆共点；

当n为大于3的奇数时，其中每n-1条直线可确定一个“n-1圆共点”的点，共有n个这样的点，这n个点共圆.

笔者曾尝试证明n=6时的情形，图形复杂到在一张A4纸上都难以画出，因此更谈不上证明，而证明上述猜想更是超出了笔者的知识范围，希望有“大家”能证明这个猜想正确或错误.