问君知悉几多美，数学自带凌云笔*

☉安徽省合肥市第四十八中学教育集团 史承灼

☉安徽省合肥市第四十八中学教育集团滨湖校区 邹太芹

数学评论家普洛克拉斯说：“哪里有数，哪里就有美.”数理逻辑学家罗素也指出：“数学，如果正常地看它，不但拥有真理，而且具有至高的美，正如雕塑的美，是一种冷而严肃的美.”数学美隐藏在单调的数字和公式中，需要通过思考才可发现它、欣赏它.关于数学美的论述很多，本文以不同的视角，谈谈教学中的数学之美.

一、数学语言的凝练之美

数学语言极其严密、精炼，有严格的界定和明确的含义，一字之差，意义相差甚远，需要用心感受数学的简约、凝练之美.

案例1：角平分线的判定定理：角的内部到角两边距离相等的点在角的平分线上.

师：角平分线的性质定理是什么？

生：角平分线上的点到角的两边距离相等.

师：它的逆命题是什么？

生：到角的两边距离相等的点在角的平分线上.

师：谁来解释一下点到角的两边的距离的含义？

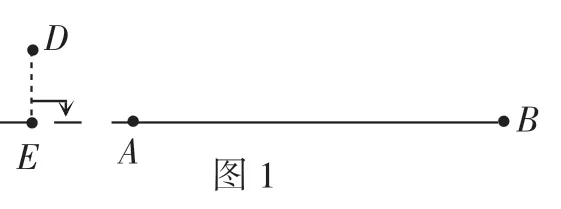
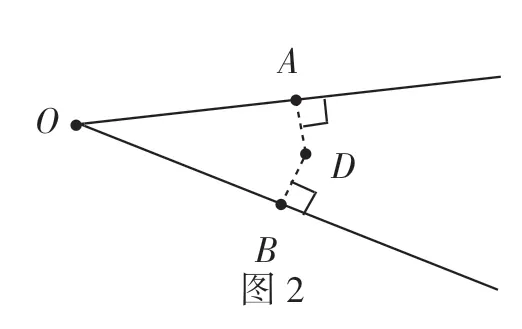
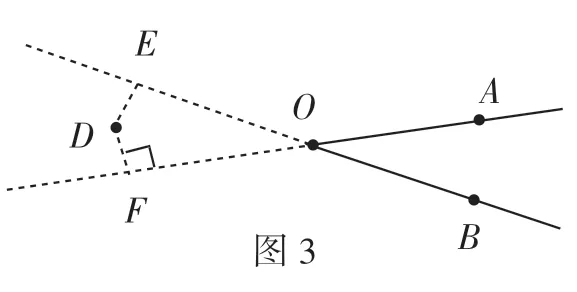
生：在图1中，点D到线段AB的距离，就是点D到线段AB所在直线的距离，所以要把线段AB反向延长，线段DE的长度是点D到直线AB的距离，也是点D到线段AB的距离，因为线段、射线都是直线的一部分.角的两边是两条射线，点到角的两边距离相等，可以理解为点到角的两边所在直线的距离相等.因此，到角两边的距离相等的点的位置有三种情况，如图2、图3和图4.

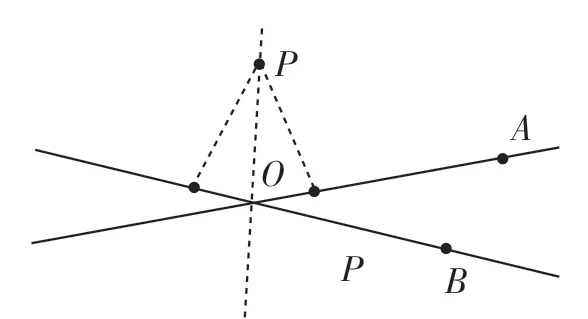
图4

师：也就是说，到角的两边距离相等的点，应该是在这个角的平分线所在直线上或这个角的邻补角的角平分线所在直线上.所以，这个逆命题还应该补充一点什么？

生：点在角的内部.

师：请完整叙述这个逆命题.

生：角的内部到角的两边距离相等的点在角的平分线上.

教师一连串追问的目的，是想让学生抓住角平分线判定定理中的两个关键词：到角的两边距离、角的内部，学生在问题的思考和解决过程中，剥茧抽丝，辨析本质，体会到数学语言的简约、凝练之美.

二、数学知识的结构之美

数学是研究现实世界中空间形式和数量关系的科学，具有高度的抽象性、严密的逻辑性和应用的普遍性.同时，数学中的概念和原理、思想和方法等，构成了一个完美的整体结构.

案例2：一元二次方程的解法、根的判别式、根与系数关系之间的内在结构.

关于一元二次方程的解法，首先可从直接开平方入手，解形如x2=b（b≥0）的一元二次方程，进而解形如（x±a）2=b（b≥0）的一元二次方程，在转化中解决问题，实现知识的小台阶推进.接下来求解类似x2+x-1=0的一元二次方程，这是一个承上启下的环节，既要借助前面的方法解决这个问题，将x2+x-1=0化归成，又要为下面的公式法求解提供方法与方向.然后求解一般形式的一元二次方程ax2+bx+c=0（a≠0），思考的方向是“如何将具体的一般形式转化为可以直接开平方的形式”！

当我们窃喜找到求ax2+bx+c=0（a≠0）的根的通法之时，新的问题应运而生.对于配好后的式子，真的可以肆无忌惮地直接开平方吗？一个悬疑，引出两个结论：（1）b2-4ac的值的情况决定方程是否存在实数根；（2）b2-4ac的值的情况决定方程实数根之间的大小关系.由（1）很自然地生成了“根的判别式”，而由根的判别式Δ=b2-4ac和求根公式，同样很自然地得到“系数与根有关系”的判断.关系具有相互性，根对系数又有什么影响呢？回到因式分解解一元二次方程中，对于方程（x-a）（x-b）=0，两根分别是x1=a，x2=b，先明确方程的根，再将方程还原成一元二次方程的一般形式x2+［-（a+b）］x+ab=0，进一步置换成x2+［-（x1+x2）］x+x1x2=0的形式，如此，不难得到猜想：如果一元二次方程x2+bx+c=0有两个实数根x1、x2，那么x1+x2=-b，x1x2=c.对于一般形式的一元二次方程ax2+bx+c=0（a≠0），根据学习经验进行化归，两边同时除以系数a得到根对系数的直接影响是对于以上猜想，可用求根公式进行严谨推理.

一元二次方程的众多知识和方法，通过它们之间的内在逻辑，成为一个完美的整体结构，这种结构之美不禁让人掩卷之余荡气回肠.

三、跨越时空的数学文化之美

数学家哈代认为，不美的数学在世界上是找不到永久容身之地的.在数学发展史上，有着太多的跨越时间和空间的殊途同归杰作.

案例3：海伦—秦九昭公式.

古希腊数学家海伦在《共制》的《度量论》中，给出了三角形面积公式：c）（其中a、b、c分别为三角形三边长，S为三角形的面积）.无独有偶，我国宋代数学家秦九昭在《数学九章》中，用表示三角形的面积.其实这两个公式的本质是一样的，推理如下：

不知道大家有没有想过，这两个公式的源头在哪里呢？真是无巧不成书，就在笔者现在所带的学生中，两名学生不约而同给出了海伦—秦九昭公式的推导过程.

已知：如图5，△ABC中，AB=c，AC=b，BC=a（a＞b＞c），AD⊥BC，垂足为点D，若BD=x，则CD=a-x.

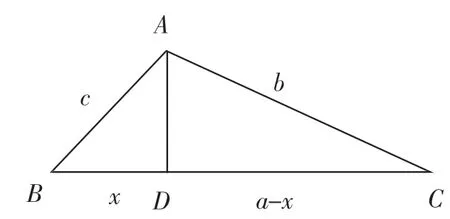
图5

由勾股定理可得c2-x2=b2-（a-x）2.

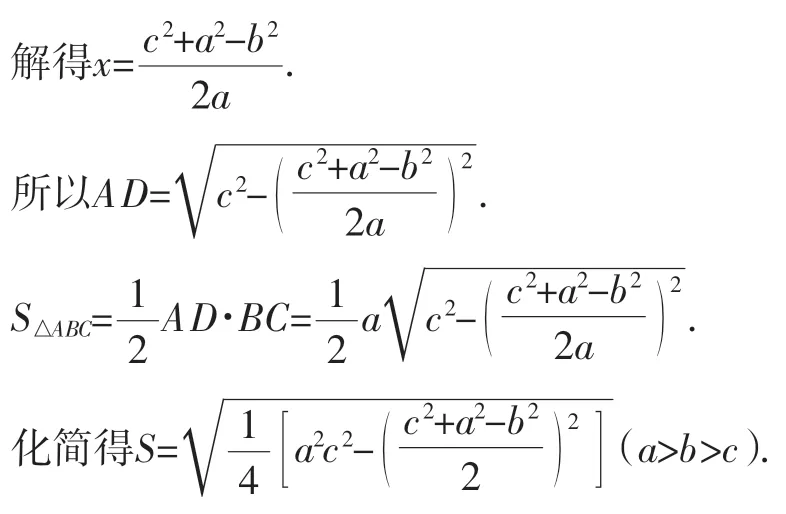
上述过程可能不完美，但两名八年级的学生能给出这样的答案，足以让人自豪.由此不仅让人感叹数学是如此的“魅惑众生”！数学的魅力真是亘古绵长、滔滔不绝.

四、数学应用的模型之美

许晨阳说：“不是我们创造了数学，而是它一直在那里，我们只是发现了它而已.”数学是一门抽象且逻辑性强的学科，而中小学生的思维正处于由具体形象思维向抽象逻辑思维过渡的阶段，所以需要教育者提供适当的学习素材，用思维和创意让学生发现数学应用的模型之美.

案例4：翻币问题：如果桌上有3枚纪念币，正面全部向上，每次将其中的2枚同时翻转，能否经过若干次翻转，使3枚纪念币的反面全部向上？

这是在学生学习了有理数加、减、乘、除、乘方运算之后，为进一步加深对有理数符号运算的理解而进行的综合实践研究.需要将实际问题抽象为数学问题，同时渗透分类、转化、类比等数学思想和方法.为了操作的方便与直观，可把“翻币问题”改为“翻转纸杯问题”.

师：取3只纸杯，杯口全部朝上，每次翻转2只纸杯，经过若干次操作，能否使杯口全部朝下？若能成功，最少需要几次？

学生小组合作，操作尝试.

师：翻转的过程，可以抽象为乘“-1”的过程.以3只杯口朝上的纸杯为例，现在摆在桌面上的3只纸杯，在你眼中是什么？

生：3个“+1”.

师：用S翻转前=（+1）×（+1）×（+1）=+1表示翻转前的情况，那么，假如反转后能使3个杯口全部朝下，应该如何表示？

生：S翻转后=（-1）×（-1）×（-1）=-1.

师：一次翻转2个纸杯，翻转过程中的结果S如何用式子表示？

生：S=（+1）×（-1）×（-1）=（+1）×（+1）=+1.

师：换句话说，每次翻转2个纸杯，相当于在S翻转前的基础上乘什么？

生：乘“+1”.

师：你能解释“3翻2”注定失败的原因吗？

生：（充分思考、讨论后）S翻转前=+1.每翻转1次，相当于S=（+1）×S翻转前=（+1）×（+1）=+1.翻转n次，相当于S=（+1）×（+1）n=+1≠-1=S翻转后，所以“3翻2”注定失败.

应用数学知识解决实际问题，首先要把实际问题中的数学问题明确表述出来，然后才能使用数学的理论和方法进行分析，得出结论，最后返回去解决现实问题.由于实际问题的复杂性，往往很难把现成的数学理论直接套用到这些实际问题上，这就要求在数学理论和所要解决的实际问题之间构建一个桥梁加以沟通，以便把实际问题中的数学结构明确表示出来，这个桥梁就是“数学模型”，这个桥梁的构建过程就是“数学建模”.

徜徉在数学的殿堂中，与美共存，师生在数学之美中共生共长，是生命的一种别样享受.