一道中考试题的多解思路探究

☉湖北省武汉市左岭第一初级中学 王晓霞

解题是人类的一项基本活动.人类有意识的思维中大部分均与题目有关.数学学习与解题息息相关.在数学教学活动中，近几年的一些中考试题、调考试题成为研究的热点.首先，这些题目的命制均来源于在数学方面有造诣的一些专家、名师，他们对知识的理解非常深刻，对数学知识的运用非常精通；其次，这些题目均与平常所做的题目或多或少有些不一样，从而在解答时候需要仔细斟酌；最后，这些题目所展现出来的知识呈现方式、思维方式、解决问题的方式均值得好好研究与学习.笔者长期在一线从事基础教育工作，研究试题是日常工作中重要的一部分，现针对2018年武汉市中考选择题第10题，谈自己的一点感受.

一、试题呈现

（2018年武汉市中考第10题）如图1，在⊙O中，点C在优弧AB上，将弧BC沿BC折叠后刚好经过AB的中点D.若⊙O的半径为，AB=4，则BC的长为（ ）.

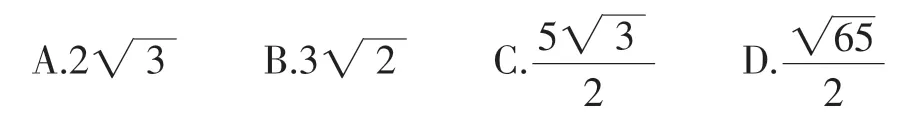
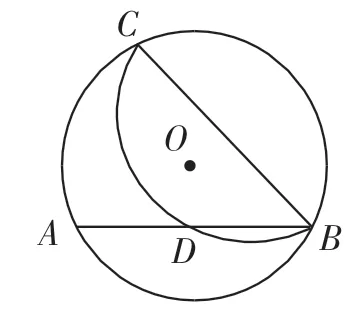
图1

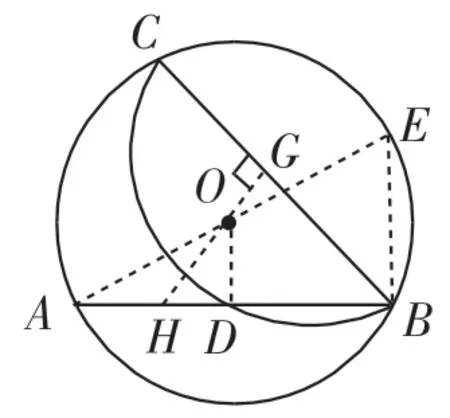
图2

二、多解思路

思路1：如图2，连接OD，作直径AE，连接BE，过点O作OG⊥BC于点G，交AB于点H.通过计算易得：BE=BD=2.因为弦BE与弦BD是等圆中的两条弦，所以它们各自所对的劣弧是等弧，即，所以与是等弧，则∠ABC=∠EBC=45°.在等腰Rt△HBG中，斜边BH=2+1=3，所以直角边BG的长为，故BC=

思路1反思：垂径定理的学习与应用可以让学生顺势而为连接OD.但只有这条辅助线此问题是无法推进的.联系题目已知条件，易想到构造直径AE，连接BE.通过简单计算发现BE=BD=2，这是一个非常重要的信息，而这个重要信息是通过计算获得的，由此展开分析，利用45°构造等腰直角三角形解决问题.

思路2：如图3，过点E作EF⊥BC于点F，连接CE.由思路1知∠ABC=∠EBC=45°.在等腰直角△BEF中，BF=EF=因为∠C=∠A，∠CFE=∠ADO=90°，所以△CEF△AOD且相似比为所以CF=AD=2，故BC=BF+CF=3.

思路2反思：思路2建立在思路1的基础之上，同样BC平分∠ABE得到特殊角45°是此解法的出发点，计算上两种处理方法均使用相似求解.

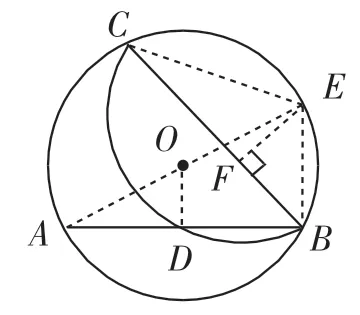
图3

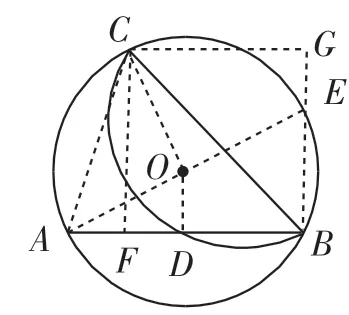
图4

思路3：如图4，在思路1的基础上，由于BC平分∠ABE，所以过点C作CF⊥AB，CG⊥BE，垂足分别为F、G.易证四边形CFBG为正方形，设正方形的边长为t.在等腰直角△AOC中，计算得AC=.在Rt△AFC中，利用勾股定理建立方程：（4-t）2+t2=（）2，求得t1=3，t2=1（舍去）.故在等腰直角△CFB中，计算得BC=3.

思路3反思：BC是∠ABE的平分线，自然联想到向角的两边作垂线，通过勾股定理建立方程求出关键线段的长，从而计算出BC.

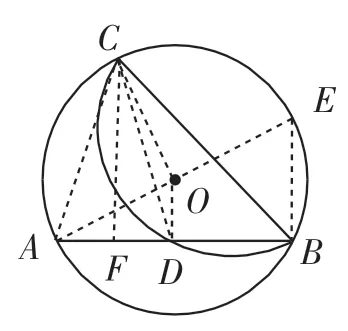
图5

思路4：如图5，过点C作CF⊥AB于点F，连接AC、CD.与所在的圆是等圆，且它们所对的圆周角均为∠ABC，所以与是等弧，故AC=DC=.在等腰△ACD中，根据三线合一，可知点F是AD的中点，所以在Rt△CDF中利用勾股定理计算出CF=3，易得BC=3.

思路4反思：∠ABC所对的弧有两段，分别为与，虽然这两段弧不在同一个圆中，但这两段弧所在的圆是等圆，从而将角的关系转化为弧的相等关系，再转化为弦的相等关系，这是本思路的着眼点.

思路5：如图6，因为∠ABC=∠EBC=45°，从而注意到AC=EC，故将△CBE绕点C顺时针旋转90°得到△CFA，则△CBE△CFA，所以∠CAF=∠CEB，FA=BE=2.因为∠CEB+∠CAB=180°，所以∠CAF+∠CAB=180°，故F、A、B三点共线，所以BF=AB+FA=4+2=6.在等腰Rt△FCB中，已知斜边，计算得直角边BC=3.

思路5反思：基于∠ABC=∠EBC，推理得到AC=EC，故使用旋转法.

思路6：如图6，延长线段BA至点F，使AF=EB，连接CF.易证△ACF△ECB，则CF=CB，∠FCA=∠BCE.因为∠ACE=90°，所以∠FCB=90°，即△FCB为等腰直角三角形，且斜边长为6，所以直角边BC=3.

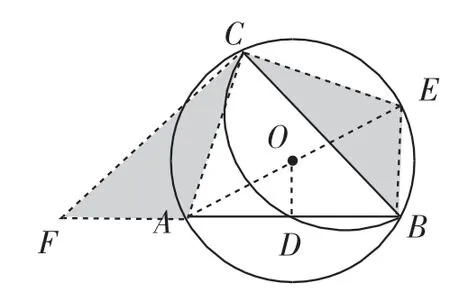
图6

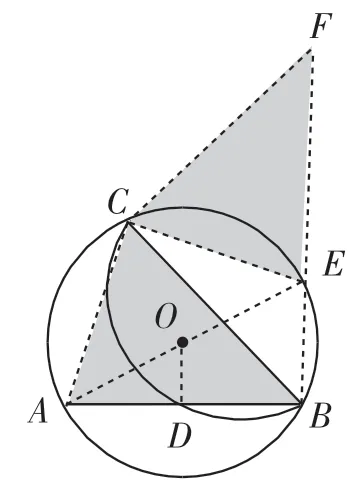
图7

思路6反思：使用补短法构造全等三角形.

思路7：如图7，类比思路5，将△ABC绕点C逆时针旋转90°得到△EFC.易证B、E、F三点共线，可知△BCF为等腰直角三角形，易得BC=3.

思路7反思：类比思路5，使用旋转法，但旋转的方向不同.

思路8：如图7，类比思路6，延长线段BE至点F，使EF=AB，连接CF.易证△ABC△EFC，简单推理即可知△FCB为等腰直角三角形，且斜边长为6，所以直角边BC=3.

思路8反思：类比思路6，使用补短法.

思路9：如图8，取点O关于直线BC的对称点O′，则O′为折叠之后的所在圆的圆心，⊙O与⊙O′为等圆，过点O′作O′E⊥AB于点E，则DE=BD=1.连接O′D、OO′、CO′，过点O作OG⊥O′E于点G，四边形ODEG为正方形，所以OG=1，GE=1.计算得O′E=2，所以O′G=1.在Rt△OO′G中，利用勾股定理，得OO′=.根据对称性，可知：HO′=，OO′⊥BC.在Rt△CHO′中，算得CH=，则

思路9反思：思路9的着眼点在于将表面的折叠问题看作一个隐圆问题，构造出这个隐圆，在隐圆中将问题解决.

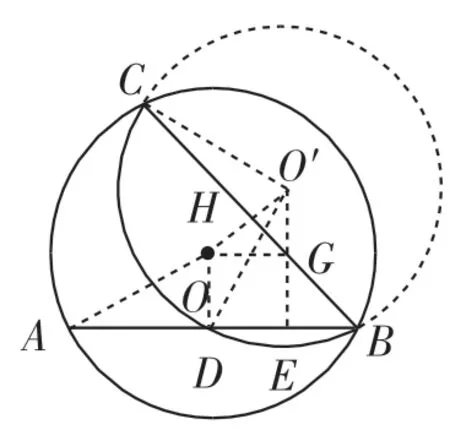
图8

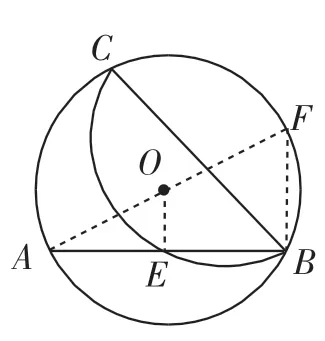
图9

三、解法升华

本题是武汉市2018年中考第10题，它的定位是一道有一定区分度、一定思维高度要求的题.本题虽然解法灵活，形式多样，但是本题的切口并不大，主要切入点在同圆或等圆中弦、弧、圆周角之间的关系.如图9，作直径AF，连接OE、BF，对学生来说是可以自然而然作出来的辅助线，通过简单计算可知BE=BF，学生难以由这两条弦相等推导出它们所对的劣弧相等，这是本题的第一个难点.另外学生不易发现与是等弧，这是本题的第二个难点.为什么会出现这种现象？主要还是学生并没有深入理解等圆的概念，学生倾向于或者更擅长处理同一个圆中弦、弧、圆心角、圆周角之间的关系，实际上它们的等量转化关系在等圆中也成立.人教版教科书九年级（上）第二十四章“圆”第一节明确指出能够重合的两个圆叫作等圆.容易看出：半径相等的两个圆是等圆.本题中实际上有两个圆，而且这两个圆是等圆.如果突破了这两个难点，这个问题就变得非常简单了，可以抽象化、一般化为图10，在⊙O中，BD是∠ABC的平分线，∠ABD=α，延长BC至点E，使CE=AB，连接DE、DC、DA，过点D作DF⊥BC，垂足为F.则△DCEﾨ△DAB，所以DE=DB.在等腰△BDE中，，所以， 即AB+BC=2BD·cosα.

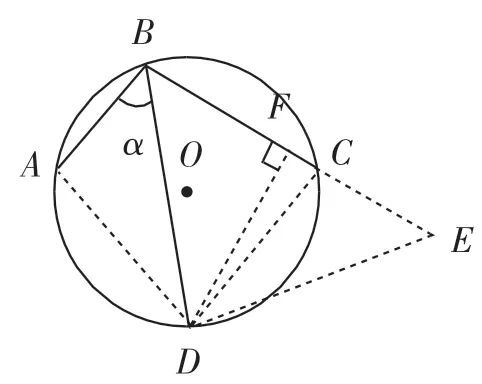
图10

本文中的考题是一个选择题，可以直接利用上述45°角时的结论求得BC=3.这样既提高准确度，又节省时间，不失为一种较好的处理方法.

四、写在最后

通过对武汉市中考试题中选择题第10题的研究发现：没有任何一个题目是完全没有见过的，虽然本题是一道有一定难度的题，但是经过分析还是能将它转化为一个比较熟悉和简单的问题，从而解决问题；任何一个看似复杂的问题也仍然是由一些比较简单的问题重组而成的，在分析时要善于步步为营地将问题分解，各个击破；解题不单纯是一种“智力活动”，其中很大程度上是对学生意志的考查，学生很多时候由于畏难情绪，丧失了解决问题的迫切需求，解题欲望下降，主观能动性不足，因而无法解决问题.所以，在数学解题过程中，要调动一切的智力因素与非智力因素，从基础知识与基本方法出发，合理分解，最终将一个未知问题转化到一个比较熟悉和比较简单的问题上来，从而解决问题.