从解法探究走向教学微设计——以一道新定义模考题为例

☉江苏省海安市城南实验中学 朱月凤

最近一次学校中考模考练习时，选用了一道新定义考题，从2019年5月北京市海淀区一模卷改编而来，前两问学生答得还可以，但最后一问普遍适应性不好.为了做好讲评工作，我们备课组先认真对该题进行了解法研究，并设计出系列铺垫式问题，取得了较好的解题教学效果.本文整理该题的一些解法探究，再给出解题教学微设计，供研讨.

一、新定义模考题的思路探究

模考题：（北京市海淀区2019年中考一模卷，改编）对于平面直角坐标系xOy中的直线l和图形M，给出如下定义：P1、P2、…、Pn-1、Pn是图形M上n（n≥3）个不同的点，记这些点到直线l的距离分别为d1、d2、…、dn-1、dn，若这n个点满足d1+d2+…+dn-1=dn，则称这n个点为图形M关于直线l的一个基准点列，其中dn为该基准点列的基准距离.

（1）略.（限于篇幅，这一小问比较简单，只是让学生初步感知“新定义”，故略去）

①若T为原点，求该基准点列的基准距离dn的最大值；

②若n的最大值等于6，直接写出圆心T的纵坐标t的取值范围.

思路探究：（2）①由P1、P2、…、Pn-1、Pn是⊙T关于直线l的一个基准点列，得d1+d2+…+dn-1=dn.则dn的最大值为⊙T上的点到直线l的最大距离.

当T为原点时，如图1，过点O作OH⊥l于点H，延长HO交⊙O于点F，则FH的长度为dn的最大值.

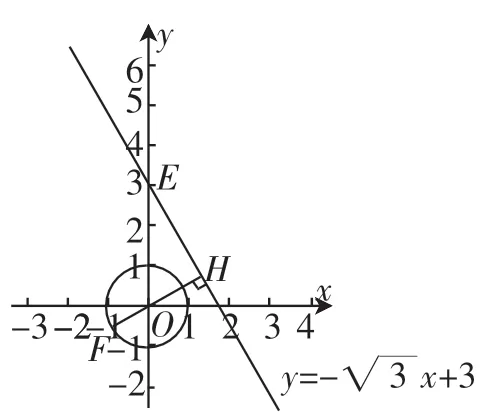
图1

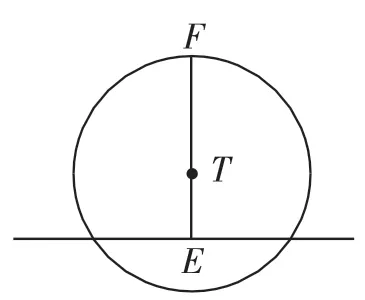
图2

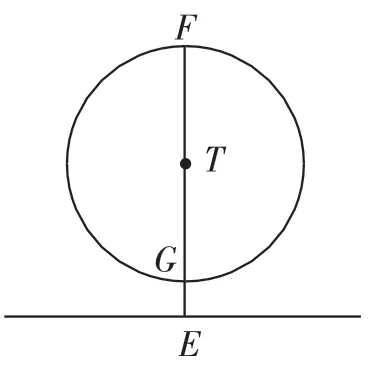
图3

②这一小问比较晦涩、难懂，让我们分析一条直线与圆的不同位置关系，如图2、图3.在图2中，直线与圆相交，此时圆上任意一点到直线的距离最大时是垂线段FE（经过圆心T），容易发现，EF＜2，且圆上能找到“很多点”（远远超出6个）到该直线的距离趋于0，这样就能找出“很多点”符合新定义，则n也就“远大于6”，这与题意不符.于是我们可以确定线段与圆应该是没有公共点的.再利用图3进行分析，此时圆上任意一点到直线的距离最大时是垂线段FE（经过圆心T），设GE=x，则FE=2+x，要使得“n的最大值等于6”，则对照定义，应该有5x＜2+x≤6x.这个不等式不太好理解，设6个点都无限接近图3中的点G，则2+x≤6x；另一方面，有5个点无限接近点G，它们的和不会超过5x，则5x＜2+x.综上，可确定GE（即x）的范围为，相应的TE（即x+1）的取值范围为

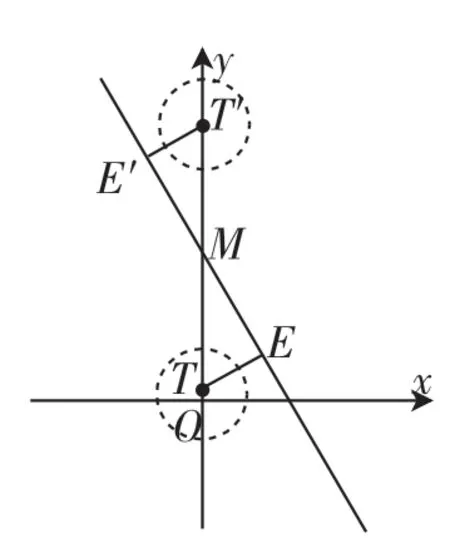
图4

解后反思：从上面的解题过程来看，从图2到图3，并分析出GE（即x）的范围为，这是本题重要进展、关键步骤，非常抽象、难懂，且涉及多个点趋向一个极端位置，对极限意识和想象能力有很高的要求.

二、围绕考题开展教学微设计

1.熟悉“定义”

出示上文“模考题”的“题干”部分，让学生先熟悉新定义，并给出简单的举例，然后给出一组基础热身题.

问题1：在平面直角坐标系中，直线l是x轴，图形M上有三点A（-1，1）、B（1，-1）、C（0，2）.

（1）判断A、B、C是否为图形M关于直线l的一个基准点列.如果是，求出它的基准距离；如果不是，请说明理由.

（2）请举出一个图形M，使得该图形M上有四个点为图形M关于直线l：y=-1的一个基准点列.

教学组织：第（1）问让学生先独立思考，再请学生上台讲解他是如何思考的；第（2）问学生设计出问题之后先在小组内由组长组织讨论、分析是否正确，然后选择符合要求的正确解答在全班交流展示，大家参与评析各小组所设计的问题是否符合新定义的要求.

2.初步运用

问题2：已知直线l是函数的图像，图形M是圆心在y轴上、半径为1的⊙T，P1、P2、…、Pn-1、Pn是⊙T关于直线l的一个基准点列.

（1）若T为原点，求该基准点列的基准距离dn的最大值；

（2）当点T的纵坐标为1时，求该基准点列的基准距离dn的最大值；

（3）当点T的纵坐标为7时，求该基准点列的基准距离dn的最大值.

教学组织：第（1）问对应着原“模考题”，跟进的第（2）、（3）问可以有效训练学生对新定义的理解，并且感受到随着圆心位置的变化，该基准点列的基准距离dn的最大值也在发生变化，为挑战下一问较难题提供初步感知.

3.挑战难题

问题2：已知直线l是函数的图像，图形M是圆心在y轴上、半径为1的⊙T，P1、P2、…、Pn-1、Pn是⊙T关于直线l的一个基准点列.

（1）举例分析n的最大值能否到5；

（3）若n的最大值等于6，直接写出圆心T的纵坐标t的取值范围.

教学组织：安排两个铺垫式问题让学生先想清如上文中提及的图2、图3这样的图形结构和性质，再有序挑战最难的第（3）问.讲评过程中，要注意让优秀学生能结合图形分析讲解，这样可以促进学生数形结合地分析这类问题，也让更多学生体会“以形助数”的分析策略.

三、关于新定义考题的解法研究与教学建议

1.新定义题的解法研究要重视数形结合分析策略

根据我们的解题研究所见，当前新定义考题热度不减，成为很多地区模考卷、中考卷的把关题型，而且新定义考题的风格各异，呈现丰富多样的地区特点，比如，北京地区以新定义为背景，关联函数图像、直线和圆的位置关系，分析参数的取值范围，引领着北京各区的模考卷也纷纷模仿命制出大量的新定义考题，这些考题又被全国各个地区引用.可以发现，这类新定义考题的解题策略中都体现了数形结合的分析策略，也体现了“少算多思”的解题特点，教师解题时，要充分借助图形分析临界状态，并善于分解、分离图形来分析参数的取值范围.

2.新定义考题解题教学时要注意预设铺垫问题

在新定义考题解题教学时切忌就题讲题，或者简单的核对答案式的讲解，或者以多数学生都会放弃最后一问为由，简单应付一下讲评过程.事实上，如果我们将最难的一问进行充分展开，不但能让较多的学生理解、学会这道习题的解法，而且在这个过程中，还能让学生复习很多基本图形及其性质、经典结论及其变式，所以还是值得花时间开展解题教学的.当然，对于“最难小问”的解题教学，要像上文解题教学微设计一样，进行充分预设，通过系列铺垫式问题，铺平垫稳，让学生拾级而上，促进学生自主发现解法，贯通思路，不仅让学生学会解这道习题，而且要在解题教学过程中让学生能学会这类新定义习题的解法，并且在这个过程中收获解题信心.

三、写在后面

近两年《中学数学（下）》刊发了不少新定义考题的教学研究文章，有效引领了一线教师的解题研究，本文就是受到类似文献［1］～［3］的影响而整理出来的.这样做，事实上也端正和加深了我们对解题研究的理解，比如，解题研究不能只是关注解法或一题多解，甚至是一些个性化的解法或者技巧性解法，而要从解法研究出发，基于学情预设解题教学微设计，以便促进学生更好地理解和掌握解法，达到做一题、通一类、会一片的解题效果.