中考数学试题中数学史内容的分析

☉太原师范学院附属中学 薛 华

☉太原师范学院教师教育学院 刘 凯

☉太原师范学院教师教育学院 陈梦瑶

一、引言

我国教育部制定的《义务教育数学课程标准（2011年版）》要求数学教材要适时地介绍数学发展史的相关材料，用以激发学生学习数学的兴趣，因此笔者对初中数学教材中融入的数学史内容做了详细的分析.该课程标准中还要求“评价应以课程目标和课程内容为依据，体现数学课程的基本理念，全面评价学生的知识技能、数学思考、问题解决和情感态度等方面的表现”，而且“试题的改编是指对已有试题的数据、面貌、内涵等方面进行合理改造，进而得到所需试题的过程，一个推陈出新的过程”.这么多年来，中考试题的编制是怎样推陈出新的？其作为重要的评价方式，又是怎样利用数学史实现对相应数学知识的考查，实现对数学思考、问题解决及情感态度的考查的？本文选取2017年各地区的中考试题为研究对象，对其中渗透的数学史内容做分析，特别关注考查的数学史内容和数学教材中数学史内容的关联，以期为初中数学教学、中考试题的编制提供一些参考.

二、2017年中考数学试题的统计分析

汪晓勤教授将数学史融入数学教材分为五类：（1）点缀式，即图片；（2）附加式，即阅读性材料；（3）复制式，即古代数学问题的直接引用；（4）顺应式，即在正文将数学问题改编为符合学情的问题；（5）重构式，即正文各部分融入数学史，数学史料经过加工变成易于学生理解的知识，是最高水平的融入.据此，本文选取2017年26个地区的中考试题，对其中涉及的数学史内容做统计分析，设置的统计类别有中考题的来源地区、题型及题次、考查知识领域、史料出处及内容，最主要的是按照样本中数学史具体的呈现方式归为四大类：一是史料的直接考查，即以史料为背景呈现考题；二是古今情境融合，即关注史料的现实情境设置考题；三是数学史料的重构，即通过对史料的适度改变建构考题；四是数学史与实用技术的融合，即沿袭我国古代数学重视与实用技术的融合而设置考题.具体呈现如表1：

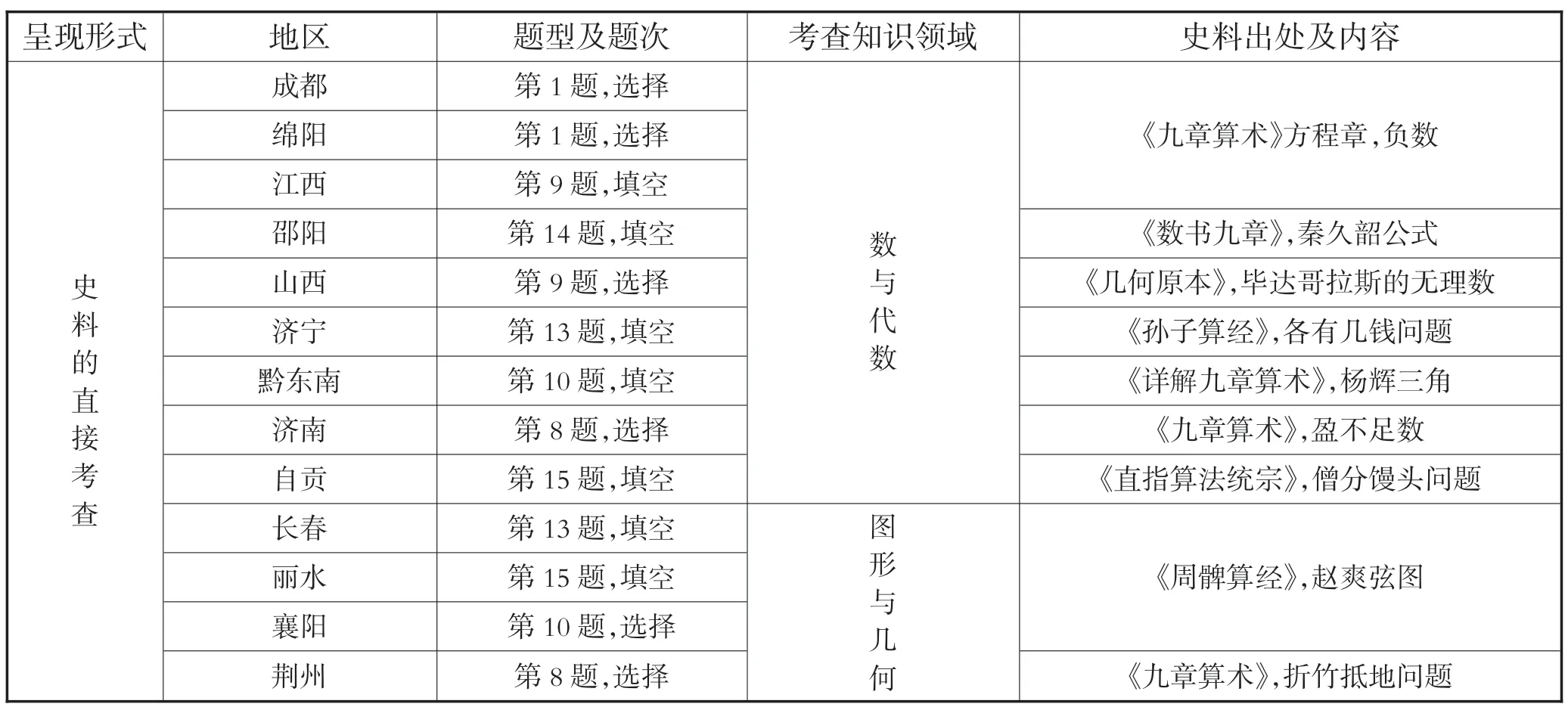
表1 2017年中考数学试题中涉及数学史考题的统计

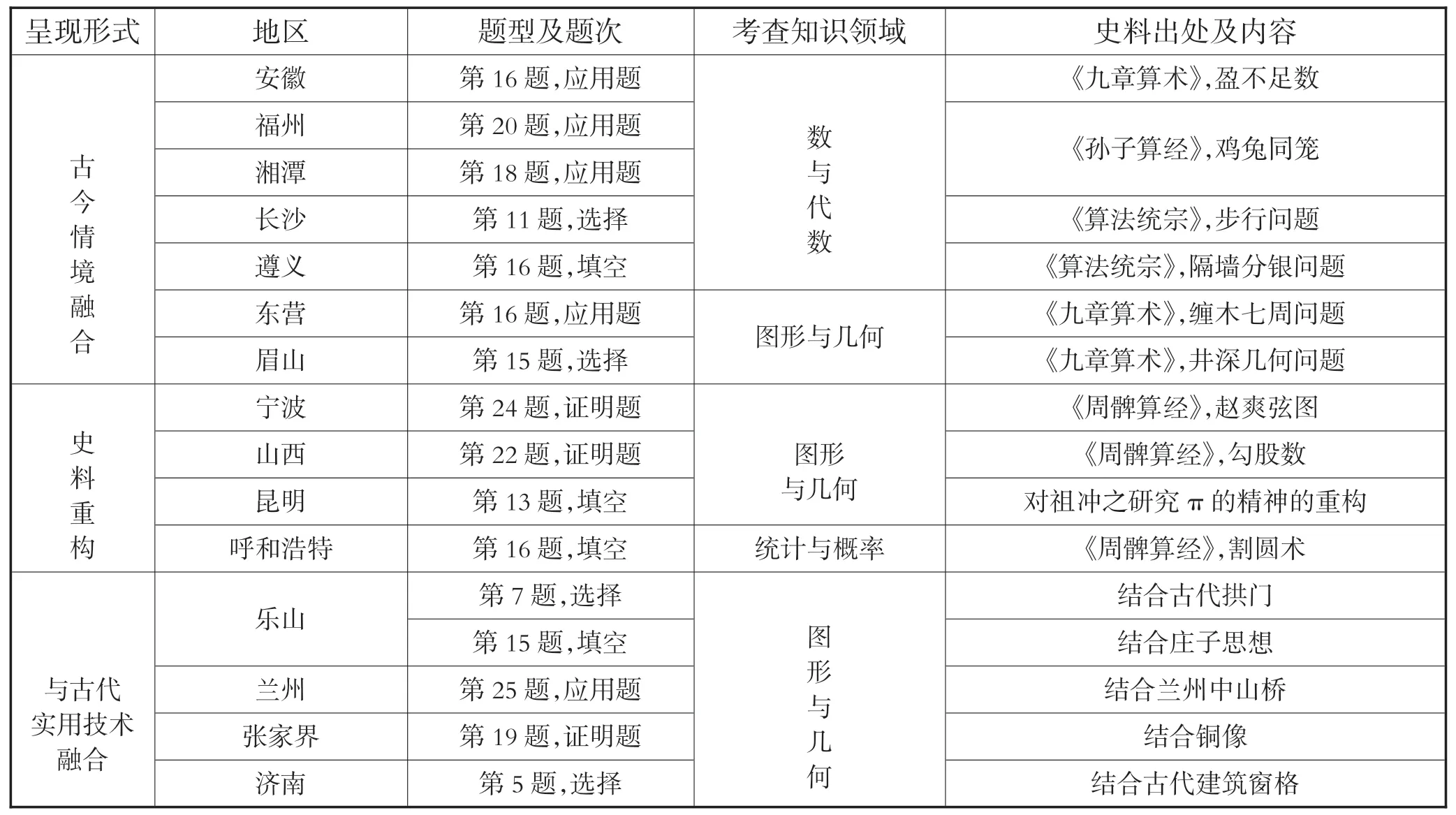
呈现形式 地区 题型及题次 考查知识领域 史料出处及内容古今情境融合史料重构与古代实用技术融合安徽 第16题，应用题《九章算术》，盈不足数福州 第20题，应用题 《孙子算经》，鸡兔同笼湘潭 第18题，应用题长沙 第11题，选择 《算法统宗》，步行问题遵义 第16题，填空 《算法统宗》，隔墙分银问题东营 第16题，应用题 图形与几何 《九章算术》，缠木七周问题眉山 第15题，选择 《九章算术》，井深几何问题宁波 第24题，证明题图形与几何数与代数《周髀算经》，赵爽弦图山西 第22题，证明题 《周髀算经》，勾股数昆明 第13题，填空 对祖冲之研究π的精神的重构呼和浩特 第16题，填空 统计与概率 《周髀算经》，割圆术结合古代拱门第15题，填空 结合庄子思想兰州 第25题，应用题 结合兰州中山桥张家界 第19题，证明题 结合铜像济南 第5题，选择 结合古代建筑窗格乐山 第7题，选择图形与几何

三、2017年中考数学试题中数学史内容分析

由上面的统计分析可知：考查的26个地区中涉及数学史的考题有29处，其中考查“数与代数”的有14处（占比48.3%）、考查“图形与几何”的有14处（占比48.3%）、考查“统计与概率”的有1处（占比3.4%）；其中选择题10处（占比34.5%）、填空题11处（37.9%）、应用题及证明题8处（占比27.6%）；从数学史内容的四大呈现方式来看，史料的直接考查有13处（占比44.8%）、古今情境结合的有7处（24.1%）、对史料进行重构有4处（13.8%）、与古代实用技术相融合有5处（17.2%）.具体中考试题分析如下：

1.试题中对史料的直接考查

2017年中考试题中涉及数学史内容的考题，以史料的直接考查来呈现的考题最多.这些试题都呈现了特定的数学知识发展的历史，学生可直观感受到数学史料，且陈述比较清晰，既考查了学生对数学史料的理解，也达到了知识的考查，但主要是对史料的直接考查.

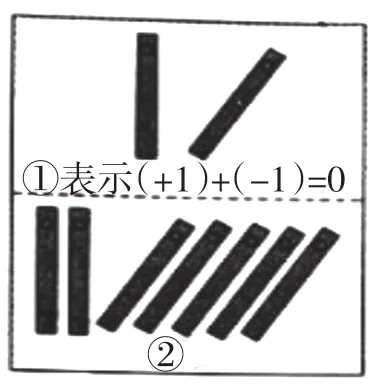
图1

例1（江西第9题）中国人最先使用负数，魏晋时期的数学家刘徽在“正负术”的注文中指出，可将算筹（小棍形状的记数工具）正放表示正数，斜放表示负数，如图1，根据刘徽的这种表示法，观察图1①，可推算图1②中所得的数值为___________.

分析：本题交代了“正负术”发展经历过程中“算筹”的表示方式，通过对“算筹”的简要描述，提出的问题既考查学生对史料的理解，也考查正负数概念及运算法则.而正负数发展经历了坎坷，公元263年刘徽在《九章算术注》中详细给出正负数的定义及运算法则，并应用算筹进行正负数计算（红色表示正，黑色表示负）.从有关记载来看，负数最早出自于我国的《算术书》，而国际上对正负数的认识如下：印度最早由婆罗摩笈多给出，并给出了正负数的乘法法则；10世纪阿拉伯著名数学家艾布·瓦发（940年—约998年）应用了负数；而西方对负数的认识比较滞后，16、17世纪大多数欧洲数学家不承认负数，例如，帕斯卡好友阿润德用反例反对负数，1831年英国数学家德·摩根仍认为负数是虚构的，到18世纪欧洲数学家才普遍接受负数，负数的合理性在逻辑上得到确立是在19世纪.

链接教材和教学：人教版七上有理数章节阅读与思考对算筹的具体介绍，涉及了刘徽《九章算术注》中有理数计算法则详细介绍.北师大版七上有理数及其运算章节的读一读中负数小吏同样讲到刘徽，还讲到国外负数发展的历程.由此看来，教师在最开始数的拓展中应关注数学教材中的阅读材料，挖掘其中的数学知识，避免学生在考试时遇见此类问题有陌生感.

2.试题中的古今情境融合

涉及古今融合的考题位居第二，古今融合就是将中考试题结合数学发展过程中的情境，但是这样的情境在今天仍然存在，仍有现实意义.学生既能了解数学史，又可以与自己的现实生活相结合，达到利用数学知识解决实际问题的目的，同时考题符合中学生的认知水平，又有数学建模的价值.

例2（湖南长沙第11题）中国古代数学著作《算法统宗》中有这样一段记载：“三百七十八里关，初健步不为难，次日脚痛减一半，六朝才得到其关.”其大意是有人要去某关口，路程378里，第一天健步行走，第二天起，由于脚痛，每天走的路程都为前一天的一半，一共走了六天才到达目的地，则此人第六天走的路程为（ ）.

A.24里 B.12里 C.6里 D.3里

分析：该问题虽是对古题的再现，但是走路问题在我们生活中每天都在发生，学生可以在做题时体会数学知识时刻存在于自己身边，同时该题考查学生对一元一次方程的理解.史料的来源《算法统宗》是明代数学家、珠算一代宗师程大位的著作，全书共17卷，完成了筹算到珠算的改革，其中运算口诀的编写，加快了运算速度，我们熟悉的“一上一，二上二，三下五去二……”则出自本书.李俨先生曾说：“在中国古代数学的发展过程中，《算法统宗》是一部重要著作，从流传的长久、广泛和深入来讲，那是任何其他数学著作不能与它相比的.”由此看出该书影响深远，著作中有更多的经典问题可供我们现在利用，如“以碗知僧”“油盐相换”，同时可用国外纸草书上的问题.

链接教材和教学：在人教版七上数学教材一元一次方程章节，例题中用到纸草书上的数学问题，“已知一个数，它的三分之二，它的一半，它的七分之一，它的全部，加起来为33，求这个数”.该题和例4中的考点及考查方式几乎一样，都涉及设未知数和通分.同样北师大版七上教材一元一次方程章节随堂练习中，由于考虑到刚开始认识一元一次方程，其对纸草书上的题进行了简化，“一个数它的全部，它的七分之一，和为19，求这个数”.从这两个典型版本教材可以看出教材中融入数学史时，编者根据学情进行了加工，而教师在教学过程中应领会编者对教材中数学史加工的意图，拓展更多以数学史为背景的练习.

3.试题与古代实用技术的融合

试题与古代实用技术融合，说明中考试题中的数学史正体现了我国数学的发展注重它的实用价值，反映在考题中可以是利用古代建筑、古代实用主义的思想（庄子无限分割思想来自于对椎的分割）等来考查数学知识.

例3（内蒙古呼和浩特第16题）我国魏晋时期数学家刘徽首创“割圆术”计算圆周率.随着时代发展，现在人们依据频率估计概率这一原理，常用随机模拟的方法对圆周率进行估计.用计算机随机产生m个有序数对（x，y）（x、y是实数，且0≤x≤1，0≤y≤1），它们对应的点在平面直角坐标系中全部在某一正方形的边界及其内部，如果统计出这些点中到原点的距离小于或等于1的点有n个，则据此可估计π的值为___________.（用含m、n的式子表示）

分析：该题在我国割圆术基础上结合了国外不同的求π的方法，对频率估计概率及确定点的坐标进行考查.历史上刘徽“割圆术”精确估算π的值，而法国人布丰则用一种十分奇妙的方法，即投针法来计算π，布丰是著名的自然科学家，但是他在数学研究中追求创新，1777年他在出版的《能辨别是非的数学实验》中提出用在白纸上投针的实验方法计算π.同样，1995年，英国的罗伯斯·马修斯利用夜空中的亮星来计算圆周率.这些数学实验，证明了圆周率π隐藏在自然界的客观规律中.

链接教材和教学：人教版九上教材概率初步试验与探究中通过在正方形的内接圆中撒米来估计π；北师大版九上教材概率的进一步认识读一读中涉及模拟实验，即利用小球代表生活中的事物或者用计算器产生数据进行模拟，都是与例题一样的原理.

图2

四、结论与建议

数学是培养学生逻辑思维能力的重要学科，它是以发展逻辑思维为主的一门学科，并且有着长久的历史发展过程，在“立德树人”的教育理念中起着重要的作用.通过对2017年26个地区中考题中数学史内容的分析，提出以下建议：

1.以《课标》为指导，以教材为抓手

考查的中考题中的数学史料，基本上在全国使用较多的各种版本的数学教材中都能找到它的踪迹，可见中考试题并没有脱离教材，并且在教材中呈现的方式都可以抽象出具体的数学模型，与中考数学题呈现方式遥相呼应，所以数学教学应紧密结合课标要求的深度，重视教材中融入的数学史料，教师应综合利用多版本教材，熟悉适用范围最广的三大版本的数学教材，在数学史料中挖掘数学知识的本质属性，在讲解数学史时不仅仅只是讲故事，而且应该把它贯穿在整个数学知识的学习中，以史料为母本，以数学名题为背景，在游戏中讲课，在游戏中轻松学习，避免现在许多教师利用导学案而忽视了对教材的关注.

2.以史为基石，情境再现，加强重构

通过统计分析可以看出以重构方式呈现的数学试题比例最小，而将数学史料通过重构式、顺应式融入数学教材的方式一直是我们期待的融入形式，同样数学中考试题的呈现也应该加强这两种方式，因为历史在发展，原有情境在我们现今生活中依然存在，我们应用好史料，让其继续为我们服务，在此基础上，由于时代在进步，并且数学题永远做不完，我们应该像宁波、山西考题那样以史料为基础，但不拘泥于固有的思路，进行更多的变形，达到一个史料为多个数学知识服务的目的.

3.关注经典，深入研究，多方交融

中考题中的数学史料均出自于中国的经典数学著作，可见《九章算术》《海岛算经》《九章算术注》《周髀算经》《算法统宗》这些经典有着不可小觑的影响力，这就启发我们一线的数学教师提高自己的专业素养，关注经典著作中的数学问题，将其转化为学生可以接受的数学知识，扩宽学生的视野，与此同时，我们发现中考试题中对国外数学史实的关注度远远不够，这就要求我们重视多元文化下的合作交流，避免盲目自信.在多国交融的基础上，还应该结合本土特点.我国试题大多结合了古代的实用性这一特点，在融入国外数学史时同样应该结合别国数学的特点，让数学“活”起来，成为富有感情的学科，成为有血有肉的学科.