基于稀疏表示及奇异值分解的水位检测系统设计

刘兆春，袁光辉，王晨旸

安徽大学江淮学院，安徽合肥,230031

近年来，图像处理、模式识别技术发展迅速，水位识别这一领域引起了相关学者们的积极关注，该领域理论研究方法也日益成熟[1-4]。但目前仍存在一些有待解决的问题，如摄像机获得的水尺图像由于拍摄距离较远、光线不好等因素导致水尺图像存在局部缺失、小角度旋转等问题，从而影响水尺图像读数，因此，本文提出一种基于稀疏表示与奇异值分解的水位检测识别算法。引入过完备字典进行图像稀疏表示的理论最早是由Mallat等人[5]提出，在应用Gabor字典基础上，结合匹配追踪算法，从而逐步逼近稀疏表示信号；2009年，Nguyen等同样基于稀疏表示提出SRBC分类器，以基于同类别低维图像运用线性编码表示测试人脸图像，该算法有效、简单，在识别分类人脸方面取得较大成功，并得到学者的普遍重视[6]。作为线性代数非常重要的组成部分，奇异值分解充分发挥了矩阵分解的作用，普遍应用于图像处理、统计学等各领域[7-8]。奇异值分解(Singular Value Decomposition，SVD )是一种非常有效快捷的提取代数特征的方法[9]，此方法中视水尺图像为矩阵并进行奇异值分解，从而得到图像矩阵的奇异值特征。Hong最早在图像识别领域运用SVD方法[10]，同时证实该法具备良好稳定性、旋转不变性及比例不变性。

为实现智能化识别水尺水位，本文基于传统水位智能识别系统，引入Hue Saturation value(HSV)空间提取技术，获取水尺目标和背景，解决了倒影对水尺部分的影响，再对图像进行预处理后，采用基于SVD及稀疏表示分类方法分类提取出目标水尺区域图像，并以此为依据计算水位值，在此基础上分类测试了旋转、缺失、部分遮挡等多组测试样本，实验证明，该算法准确有效。

1 原始图像预处理

1.1 水尺图像增强

由于水尺设于室外并与摄像机有一段距离，所以在摄像机采集图像的过程中会受到外界干扰。例如天气条件恶劣，可能会降低摄像机拍摄图像的质量，距离较远图像拍摄不清楚或是障碍物部分遮挡等问题，这会影响到后续目标水尺区域提取。故本文先对图像进行增强处理，结果见图1所示。

图1 原始图像及增强后图像

众所周知，在水面很清澈的情况下，水尺易出现倒影。这一自然现象会影响算法识别水尺倒影。所以在水位识别算法中引入HSV色彩空间模型。该模型基于色彩与各光照场景中待测目标的特点，具有相对稳定的色调值[11]。因此基于HSV色彩空间，可显著分离出水尺及其水尺倒影区域。本文将增强后的图像转换到HSV色彩空间之后，对图像的S分量进行二值化处理，如图2所示。

图2 水尺区域粗略定位

1.2 水尺定位和裁剪

从形态学角度说，膨胀指的是通过与物体边缘各点进行连接，实现边界的向外扩张[8]。膨胀的数学表达就是求局部最大值：将图像A与核B进行卷积。其中核B可以是任何形状和大小，它有一个单独定义出来的参考点，核B与图形A卷积即是计算核B覆盖区域的像素点最大值，把这个最大值赋给参考点指定的像素。这样可使图像中的高亮区逐渐增大。其数学表达式如下：

S=A⊕B={x,y|Bxy⊆A}

(1)

由图2(a)可看出，面积最大的部分是水尺部分的二值图像区域。基于此，针对水尺区域，利用形态学进行膨胀操作，从而连通水尺部分，接着提取最大连通区域就能粗略定位出水尺部分。二值图图2(a)经过两次膨胀操作后结果如图2(b)所示，对图2(b)中的连通区域面积进行计算，从而明确水尺目标所在区域，其为最大外接矩形。

同一视频流中具有存在水面波动的多帧图像，同时水尺静止。本文算法充分运用这一特点，差分累计多帧水尺图像，针对累计像素值分别采用平滑函数[12]、能量函数计算，从而分析水面波动位置的像素变化，结合定位水位线，进而在截取出的外接矩形中更准确地提取水尺目标图像。实验中，根据水尺长宽比例，分析可知水尺宽度与两个“E”的比例是8∶10，在此基础上获取水尺外接矩形目标区域，并以5∶4的比例基于水位线底边缘找到兴趣目标图像并截取，如图3所示。

图3 提取出水尺目标区域

2 基于奇异值分解及稀疏表示的水位智能识别

2.1 奇异值分解

对矩阵A∈Rm×n中以r为秩的，进行正交矩阵U∈Rm×n，V∈Rm×n，使得

(2)

成立。其中:

U=(u1,u2,…,um)∈Rm×m;V=(v1,v2,…,vm)∈Rn×n;Δ=diag(σ1,σ2,…,0,0,…0),且有σ1≥σ2≥…σr≥σr+1=σr+2=…=σp=0(p=min(m,n));VT是矩阵V的转置。这里σi(i=1,2,…),r均是实数，为矩阵A的奇异值；ui,vi是矩阵A属于σi的左右奇异值向量；对矩阵A的奇异值σi按照由大到小顺序排列得到向量(σ1，σ2，…，σr)T。

该奇异值特征向量是矩阵A的相关值，从图像a的角度分析，如果与之对应的图像矩阵是唯一的，那么原图像所对应的奇异值向量也是唯一的，所以该数值特征可用于描述灰度值图像a，图像奇异值特征向量可用于说明图像的整体信息，同时，一般聚集于k个奇异值向量值前，所以，本文提出一种局部与整体结合的特征提取方法:即将图像分块，按由上到下、由左至右的顺序排列后分别对图像每块先进行单独的奇异值分解，获得每块图像局部奇异值特征向量，接着把整体图像奇异值特征向量加至排列好的向量末尾处，从而得到局部与整体结合后的特征向量。

2.2 稀疏表示

稀疏表示主要是使用简洁的表达方式对原始信号进行信号的重构[13]。结合数学表达，即y=Ax、利用x∈Rn表示y∈Rm×l，其解决问题的核心即求x最小l0范数。

(3)

其中，‖·‖0代表l0范数，具体可用于表示向量所包含的非零项，其强调个数。求解最小l0范数涉及多方面的问题，属于NP难。一般可运用迭代贪婪追踪算法近似求解获得最小范数[14]。分析最新的压缩感知理论、稀疏表示等相关理论可知，如获得足够稀疏的x0解，则相当于可通过求解最小l1，而获得最小值的l0范数。

(4)

l1范数最小值问题可使用标准线性规划方式在多项式内求得。

(5)

2.3 基于SVD及稀疏表示水位识别流程

.3.1 训练阶段流程

输入：待训练样本图像集；输出：训练后过完备字典。

(2)利用公式(1)对训练样本整体进行奇异值分解，得到图像整体的奇异值特征向量Bi=(b1,b2,…,bk)T。

2.3.2 识别阶段流程

输入：结合D、y，分别用于表示测试样本、完备字典； 输出：具体指经识别而获取的图像。

(1)对测试样本y进行分块处理(分块方法和训练阶段相同)，利用公式(1)对每块区域进行奇异值分解，得到每块区域的奇异值特征向量Am=(a1,a2,…,a16)T(m=1,2,…,16),即为图像局部的奇异值特征向量。

(2)利用公式(1)对测试样本y进行奇异值分解后得到图像整体的奇异值特征向量Bi=(b1,b2,…,bk)T。

3 实验结果分析

训练样本的选取方面。本文主要以3～8的水尺数字，划分跨度2 cm为一类，共计25类，水尺样本每类包含10幅图像。每幅图像宽度92像素，高度112像素。实验采用分块方法如下: 每幅图像分成16块来提取局部奇异值特征向量。每块宽23像素，高28像素。

通过计算重构残差可实现正确分类图像。分析图4(e)可知，横坐标表示图像类别25个，纵坐标表示残差值，对比第11类图像可知，测试图像的残差最小，但是与其他类别的图像存在较大的残差差异，所以对应的可将此类测试图归属为第11类。图像中起始水位读数为30 cm，故第n类图像所表示的水位值可以由式LEV=31+2(n-1)计算得到。

由于水尺长时间浸于水中，有可能出现数字不清、部分区域腐蚀或水流而引起角度旋转等方面的问题[16]，本文算法基于原始水尺兴趣目标图像，对图像局部进行处理，如旋转小角度、部分图像缺失、遮挡等，在此基础上分类测试几种图像。通过分析，得出图4(b)～4(d)的结果。这可说明针对干扰图像可使用稀疏表示方法进行正确分类。对比重构残差结果，如图4(f)～4(h)所示，基于无遮挡图4(e)的情况下对比重构残差，可分析经相关处理后对比第11类图像残差的大小、最小值并未发生显著的改变，这充分说明在水尺分类方面稀疏表示所表现出来的鲁棒性，能够有效避免分类识别图像受模糊、遮挡、小位移等因素的影响。

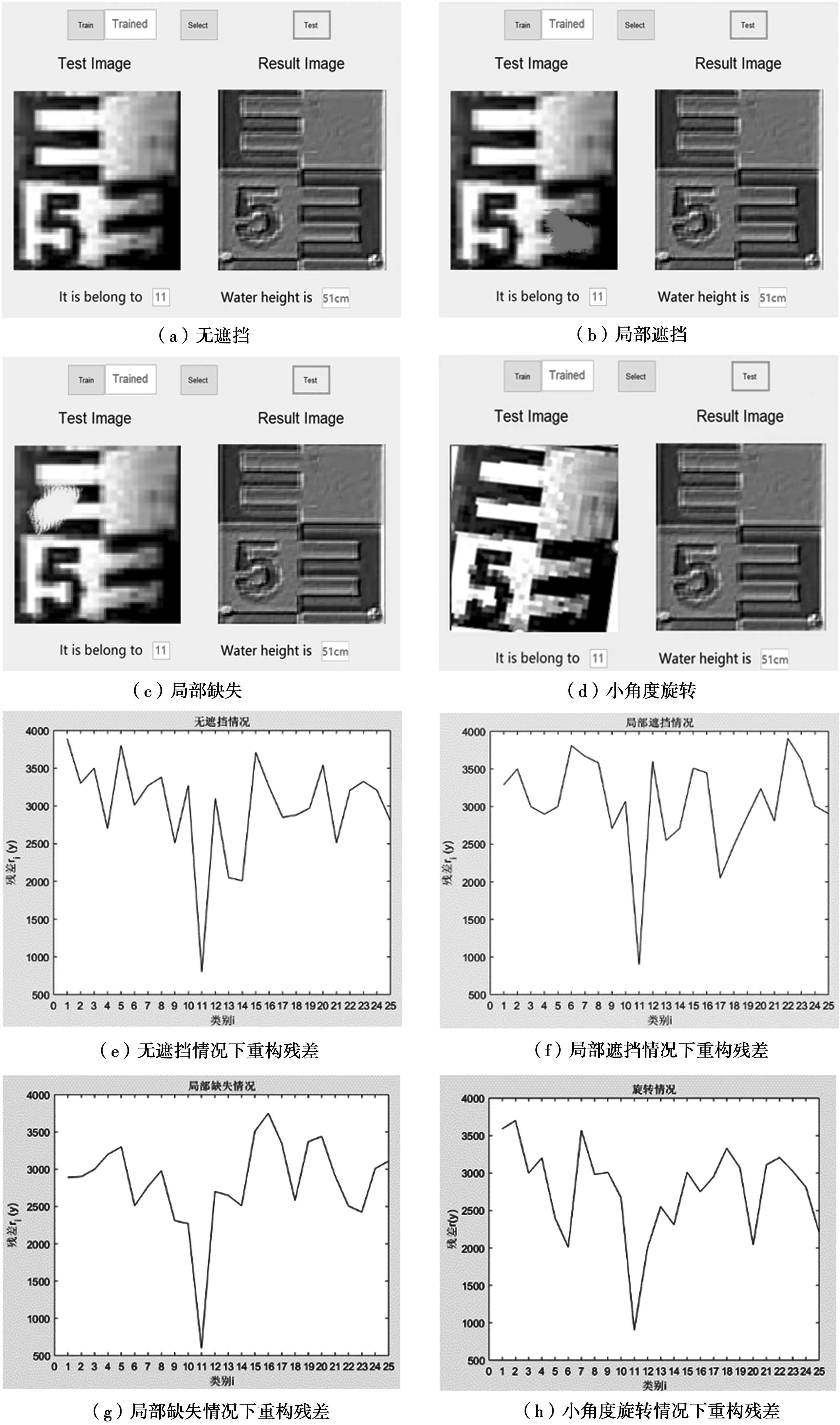
图4 分类实验结果

由于应用奇异值分解得到的奇异值特征具备良好的稳定性，因此算法对由图像噪声、图像旋转等引起的灰度变化具备不敏感特性。算法误差大约在1 cm左右,且能够有效解决倒影问题。

4 结 语

本文在HSV空间通过形态学预处理提取出水尺目标区域，利用图像局部与整体奇异值构成图像的特征向量，然后利用稀疏表示进行分类，最后根据分类的结果得到水位值。实验结果表明：本文算法对水尺刻度不清及旋转等情况有较强鲁棒性，可以对较远距离获取的水尺图片准确有效地进行水位识别。实验结果误差在1 cm左右，满足水利行业对水位值高度的计算要求，可以广泛地运用在各个监测点的水位监控系统中。