基于布谷鸟算法的数字散斑相关方法优化

唐家福， 穆平安， 周天媛

(上海理工大学 光电信息与计算机工程学院， 上海 200093)

数字散斑相关方法(Digital Speckle Correlation Method，DSCM)又称数字图像相关方法(Digital Image Correlation Method，DICM)，是一种对位移和形变的光学非接触测量技术，最早在1980年代由Ranson[1]和Yamaguchi[2]等人分别独立提出。DSCM是通过对变形前后物体表面两张散斑的灰度信息进行相关运算，对变形前后的灰度图像匹配并建立其对应关系，然后通过这一对应关系搜寻对应点，经过数值运算即可获得位移和形变信息。空域上数字散斑相关方法研究的主要内容是对相关系数中极值点搜索算法的研究。基于经典数学理论的搜索算法[3-5]主要有粗细搜索法、爬山搜索法、十字搜索法、Newton-Raphson迭代法等。十字搜索法[6]将逐像素二维搜索转变为一维搜索，大大减少了计算量。Newton-Raohson迭代法[7]对位移及应变量同时搜索，但是有许多冗余计算，计算速度变慢。爬山算法沿着领域的极值方向搜索，搜索速度快但容易出现往复搜索的情况。由于相关系数的分布有多个峰值，传统搜索算法容易陷入局部最优。随着现代数学理论的不断引入，许多新的搜索算法被相继提出，如遗传算法[8-9]、粒子群算法[10]、傅里叶变换[11]等。遗传算法精度比较高，但计算速度比较慢。容易丢失种群多样性。粒子群算法包含并行计算思想，但不容易收敛。基于傅里叶变换的频率搜索法速度快，精度高，但需要设计合适的滤波器。布谷鸟算法(Cuckoo Search，CS Algorithm)是由YANG等[12]于2009年提出的新型启发式智能算法，是一种通过模拟布谷鸟的寄生育雏方式求解最优化问题的算法。布谷鸟算法通过Levy飞行获得下一代个体，由于Levy飞行的长短变步长相间的特点决定了布谷鸟算法不易陷入局部最优值，但是后期布谷鸟算法收敛速度变慢。本文将布谷鸟算法与爬山搜索算法结合，加快了其后期的收敛速度，通过模拟散斑平移和实际散斑实验来验证算法是否能够跳出局部最优。

1 数字散斑相关方法原理

数字散斑相关方法以变形前原图像散斑场的某一点I(x,y)为中心，周围区域M(x+Δx,y+Δy)为子图像，以相关系数为代价函数，对变形后散斑图像进行搜索，获得子图像的最佳匹配区域M′(x+Δx,y+Δy)，对子图像对进行相应的数值运算可获得位移和应变。皮尔森相关系数(Pearson correlation coefficient)也称皮尔森积矩相关系数(Pearson product-moment correlation coefficient)，皮尔森相关系数更能突出相关系数的单峰峰值，精度高，所以本文选择皮尔森相关系数为代价函数，即

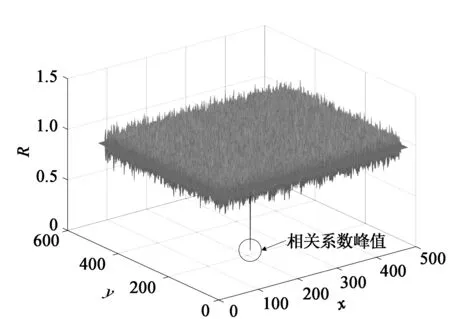
图1 相关系数分布图

(1)

皮尔森相关系数的范围为-1～1，当相关函数值等于1时，称这两个子区完全相关；当相关函数值等于0时，则称这两个子区完全不相关；当相关函数值等于-1时，称这两个子区负相关。本文利用S=1-R，将相关系数的范围调整到0～2，进而将该问题转化为求S的最小值。取出一块散斑图像子图，在其共轭散斑图像中逐像素遍历搜索相关子图，可得一个子图的相关系数分布(图1)。

2 布谷鸟算法

2.1 布谷鸟算法

为了便于模拟布谷鸟寻窝行为，假定了三条基本准则：

(1)每个布谷鸟一代只产一个蛋，并随机选择鸟窝以寄生的方式养育；

(2)在随机选择的一代群体中，最好的子代才能繁衍下一代；

(3)鸟窝数量N为定值，鸟窝宿主能发现寄生鸟蛋的概率Pa∈[0,1]。

布谷鸟寻找寄生鸟窝的位置更新公式为

Xt+1=Xt+α⊗Levy(s)，

(2)

其中Xt表示第t代的鸟窝位置，⊗为点对点乘法，α表示步长控制量，Levy(s)为Levy随机搜索路径。

根据准则(3)，当宿主鸟发现寄生鸟后，无论解的质量如何都被舍弃，为了保证一代群体数量不变，新建鸟窝即加入新解，这个位置普遍采用偏好随机游动的方式，即利用了其他鸟窝的相似性。新建鸟窝的位置更新公式为

Xt+1=Xt+r⊗Heaviside(Pa-ε)⊗(Xi-Xj)，

(3)

其中r、ε是服从均匀分布的随机数，Heaviside(x)是跳跃函数，Xi、Xj是其他任意的两个鸟窝位置。

(4)

2.2 改进布谷鸟算法

在二维数字散斑相关方法的整像素搜索过程中，Levy随机步长一般不是整数，需要在Levy随机步长的计算之后再进行一次取整。为了加快全局搜索能力，在两幅共轭图像上设定隔离边界，保证一个布谷鸟个体只在各自的区域进行搜索而不会重复搜索同一个区域，于是每一个子代个体更新公式为

图2 平面内Levy飞行随机步长分布

改进布谷鸟搜索算法流程如下：

(1)对图像划分网格设定搜索隔离边界，初始化群体位置，计算相关系数，初始化全局最优解；

(2)根据公式(5)更新子代布谷鸟群体位置，随机步长由公式(4)产生，计算相关系数，计算局部最优解，比较局部最优解与全局极值大小并更新全局最优解r；

(3)根据2.1节的准则(2)和准则(3)随机丢弃部分个体解，并由公式(3)补充群体数量；

(4)判断是否达到迭代准则，否则返回第(2)步。

在数字散斑相关方法的搜索中，如果迭代准则设置过于严格，会导致收敛速度变慢；迭代准则设置宽松，则无法搜索到准确的峰值。本文选择的迭代准则为相关系数值，设置合适的相关系数阈值，本文设定阈值为0.5，通过布谷鸟算法搜索峰值附近的位置，进一步利用传统搜索算法快速收敛到峰值。传统搜索算法容易陷入局部最优值，通过布谷鸟算法避免了这一点，但布谷鸟算法后期收敛速度将会变慢，选择一个合适的收敛准则搜索到峰值附近的一个位置，再利用爬山搜索算法快速收敛搜索到峰值位置。

3 仿真与实验验证

3.1 刚体平移仿真

利用计算机将一幅散斑图像在x方向(水平向右)和y方向(竖直向下)分别平移10个像素和11个像素，如图3所示。

(a) 平移前 (b) 平移后图3 理论平移散斑测试实验

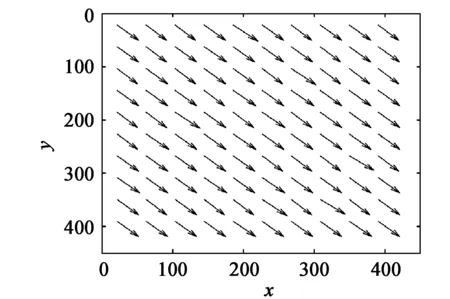
图4 位移矢量图

对上述两张理论位移图像进行分析，然后对位移矩阵进行数据统计，求解出在两个方向上的位移解的平均值。由于理论散斑图像的平移，使得原照片的右边缘和下边缘丢失一部分。这一部分在统计中被舍去。经过统计，除了在右边缘有两个点相关系数高于阀值0.5，不能准确匹配到相应点，其余点均准确地匹配到像素点，但是由于是散斑边缘，而边缘在测试过程中一般不作为测试范围，因此这两个点对于测试影响不大。根据U、V位移矩阵绘制出位移矢量图，绘制的理论平移实验的位移矢量图如图4所示。

3.2 刚体平移实验

想要测量实际位移量的大小，必须对照相机系统进行标定，将毫米尺放置在散斑表面即可完成标定。利用模拟散斑制作软件制作合适大小和密度的散斑，我们制作了不同质量的散斑进行实验，由于散斑质量的不确定性对于测量结果具有较大的影响，需要进行多组重复实验，去除不合理结果再求均值。具体的刚体平移实验步骤如下：

(1)利用散斑软件制作散斑，并利用激光器打在试件表面；

(2)搭建好实验平台，调整最佳焦距和光照，利用标尺标定出单位像素与单位长度的对应关系；

(3)采集试件散斑在T1时刻的散斑图片；

(4)移动一定距离试件，记录试件散斑在T2时刻的散斑图片，计算刚体位移并重复实验。

采集照片分辨率为640×480，纵向是480像素，通过标定尺标定计算出一个像素约为0.142 71 mm。如需获得更高精度，使用更高精度的标尺即可。其中一组采集到的散斑图像如图5所示。

(a) 平移前 (b) 平移后图5 实验测试试件前后的散斑图像

对散斑做了若干组平移测试，其中两次平移结果如表1所示。

表1 DSCM实验数据

通过与上述结果类似的多组实验，发现随着位移量的增大，其误差也逐渐增大。这是由于散斑的逐渐平移，导致一部分散斑离开照相机的拍摄范围，所以一般需要保证拍摄散斑一直在照相机范围内。实验表明在采用分度值为1 mm的标尺的情况下，精度可以达到1 mm，即将布谷鸟搜索与爬山搜索组合应用到数字散斑相关方法的搜索中能够有效测量位移量。

4 结 论

传统DSCM方法容易陷入局部最优，而布谷鸟算法能够跳出局部最优，但是在算法后期速度将会变慢，而传统搜索算法如爬山搜索法收敛速度极快，但容易陷入局部最优，无法搜索具有多极值的相关系数峰值。本文将二者结合，扬长避短，不仅能够跳出局部最优，而且能够快速收敛。通过仿真验证了算法的正确性，通过实验证明了算法精度满足要求。