双螺杆压缩机的动力学性能研究
2019-08-30赵佳磊李志峰
赵佳磊, 李志峰
(陕西理工大学 机械工程学院, 陕西 汉中 723000)
我国螺杆压缩的发展起源于20世纪80年代,因其结构紧凑、运转稳定、维护方便、寿命较长等优点,在国内占据了大量的市场份额[1]。螺杆压缩机可以分为有油螺杆压缩机和无油螺杆压缩机,无油螺杆压缩机的阴、阳转子由一对同步齿轮带动,阴、阳转子之间互不接触;有油螺杆压缩机的螺杆腔体内部喷有大量的润滑油,其阴转子由阳转子直接驱动[2]。
国内外许多学者对螺杆压缩机进行了大量研究。邢子文[3]分析了螺杆转子啮合条件并给出了阴、阳螺杆转子型线设计的一般方法;D. Zaytsev等[4]推导了一种双螺杆压缩机转子轮廓的成形方法;龙骥等[5]提出了利用自由曲线代替传统规则曲线来获得更高自由度和曲线连续性的型线;李海林等[6]对螺杆转子的速度传动比进行了验证。
综上可知,目前对压缩机螺杆转子型线研究较多,而对压缩机的动力学分析研究相对较少。本文通过计算压缩机螺杆转子截形,建立压缩机虚拟样机,在ADAMS软件中对其进行运动学分析和验证。
1 螺杆转子截面型线
1.1 啮合原理
阴、阳螺杆转子的啮合原理与直齿轮相似,都可以将其投影到垂直其轴线的一个平面内,在该平面内进行二维截面的啮合计算,与直齿轮不同的是螺杆转子在空间上具有扭转角,而直齿轮没有,如图1所示。
图1中Ⅰ和Ⅱ为两齿轮的瞬心线,O1和O2为齿轮旋转中心,1和2分别为其齿廓,Q为两齿廓某一时刻的接触点,P点为其瞬心点,v12为其切点的相对速度。根据齿廓啮合基本定理(Willis),相互共轭的两齿廓在传动的任意一时刻,它们在接触点的公法线必然通过瞬心点P,且P点在O1O2的连线上。
1.2 坐标变换
如图2所示,假定阳转子以O1为原点的坐标系(O1-x1,y1),与阳转子一同旋转;阴转子以O2为原点的坐标系(O2-x2,y2),与阴转子一同旋转。
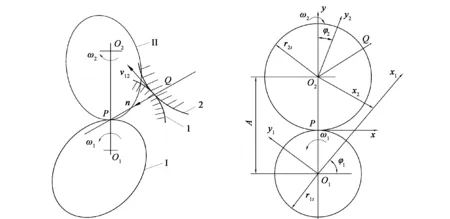
图1 齿廓啮合基本定理 图2 坐标变换原理
起始位置时y1轴、y2轴与y轴重合,x1轴、x2轴与x轴平行。当阳转子开始转过φ1时,阴转子与其对应转过φ2,Q点在三个坐标系中的位置分别为(x,y)、(x1,y1)和(x2,y2),其坐标变换关系可用下式表示(由于二维坐标系中只有x和y两个参数,不能构成3×3矩阵,故引进参数t,令t1=t2=1):
(1)
1.3 阴、阳转子型线
本文以双边对称圆弧型线为研究对象,根据上述(1)式可推算阴、阳转子截面的各段组成曲线,由于公式较多不作详述。通过MATLAB编程求解,可得阴、阳转子的端面截形如图3所示。
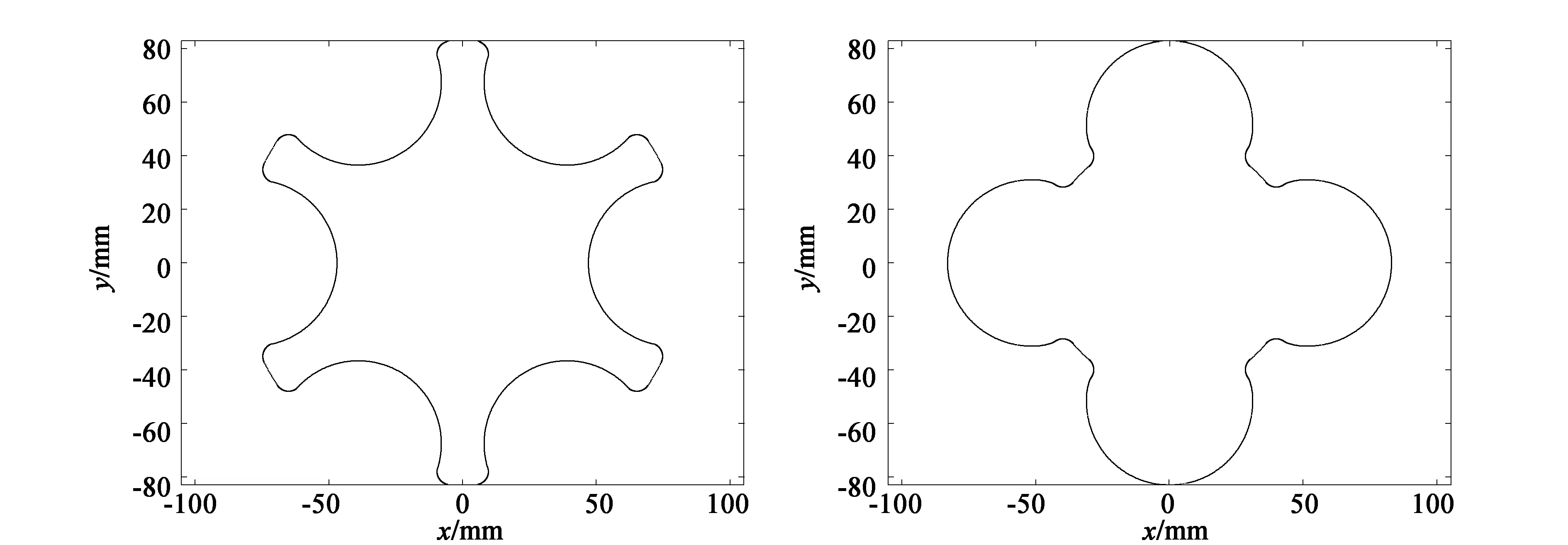
(a)阴转子 (b)阳转子图3 阴、阳转子端面截形
2 三维建模
将计算所得数据保存在记事本中,扩展名修改为“txt”格式。在SolidWorks软件中新建模型,将阳转子型线的数据点导入,进行数据的拟合,得到阳转子的端面型线;同理,可得阴转子端面型线。
螺杆的导程可用如下公式[7]计算:
T=2πRcotβ,
(2)
其中T为阴、阳转子螺旋线的导程,R为螺杆转子圆柱面的半径,β为阴、阳转子的螺旋角。
将阴、阳各参数分别代入式(2)求解参数,可求得阳转子的螺旋线导程和阴转子的螺旋线导程;根据其计算所得导程,分别进行螺旋扫描拉伸可求得阴、阳转子的实体模型,建立起阴、阳转子装配模型,并对其进行干涉检查,无误后方可进行下一步。
3 ADAMS仿真
将SolidWorks建立螺杆压缩机三维装配模型进行简化得到虚拟样机模型,保存为“parasolid.x_t”格式,导入ADAMS,其虚拟样机模型如图4所示。

图4 虚拟样机
阴、阳转子和壳体的材料均为“steel”,具体参数如表1所示。

表1 “steel”物理参数
3.1 约束设置
(1)固定副:实际工作中螺杆腔体是通过螺栓固定连接的,故将螺杆腔体和大地之间设置为固定。
(2)旋转副:阴、阳转子分别和螺杆腔体创建转动副,旋转副中心选择阴、阳转子各自重心位置,允许其可绕自身轴线转动,约束其他空间5个自由度。
(3)接触力:由于喷油式压缩机实际工作中,以阳转子拖动阴转子运动,故在ADAMS中添加碰撞力。只有保证设置合理的接触参数,才能求解更加精准的结果,其具体计算[7-8]如下。
刚度系数(Stiffness)是描述外部载荷作用下螺杆产生的弹性变形的基本物理参数,具体计算公式如下:
(3)
其中E为综合弹性模量:
由于阴、阳转子材料相同,泊松比μ1和μ2相等,均为0.29;弹性模量E1和E2相等,均为207 GPa。R为综合曲率半径:
R1、R2分别为阴、阳转子在接触点处的曲率半径。

表2 接触参数
计算可得刚度系数为1.084×106N/mm3/2;碰撞指数(Force Exponent)用来描述材料非线性程度,金属与金属材料之间的碰撞指数选取为 1.5;最大阻尼系数(Damping)描述材料的阻尼属性,一般选取刚度系数的0.1%~1%;切入深度(Penetration Depth)表示阴、阳转子在最大阻尼时转子表面侵入深度。具体数值设置如表2所示。
由文献[9]知阴、阳转子在润滑状态下的动摩擦因数为0.05,静摩擦因数为0.06。
(4)驱动设置:喷油式螺杆压缩机实际工作中以阳转子为驱动轴,故在Motion中添加阳转子转速为1500 r/min,转化为“(°)/s”如下:
直接设置较大的恒定转速和恒定转矩,曲线很容易就会发生突变或者直接出错,故设置阳转子角速度函数为STEP(time,0,0,0.2,-9000 d·time),即在0~0.2 s内角速度增加至9000 (°)/s后保持不变;阴转子为输出轴,添加负载转矩STEP(time,0,0,0.2,-10 000 N·mm),即在0~0.2 s阴转子负载转矩平稳增加至-10 000 N·mm后保持不变。
3.2 结果分析
进行仿真测试,设置End Time为0.5 s,STEP Size为0.005 s。阳转子和阴转子的传动比为4∶6,计算可知阴转子角速度应为6000 (°)/s。
ADAMS中测得阴转子在0.5 s内速度和加速度变化如图5所示,图中阴转子在启动0.2 s内加速度和速度变化幅度很大,这是由于转子在启动的瞬间碰撞冲击较大造成的。由于阴、阳转子是定传动比转动,0.25 s后加速度逐渐趋于0,符合加速度要求。仿真测得阴转子转速均值为5 985.13 (°)/s,与理论计算值6000 (°)/s误差为0.25%,满足传动比要求。
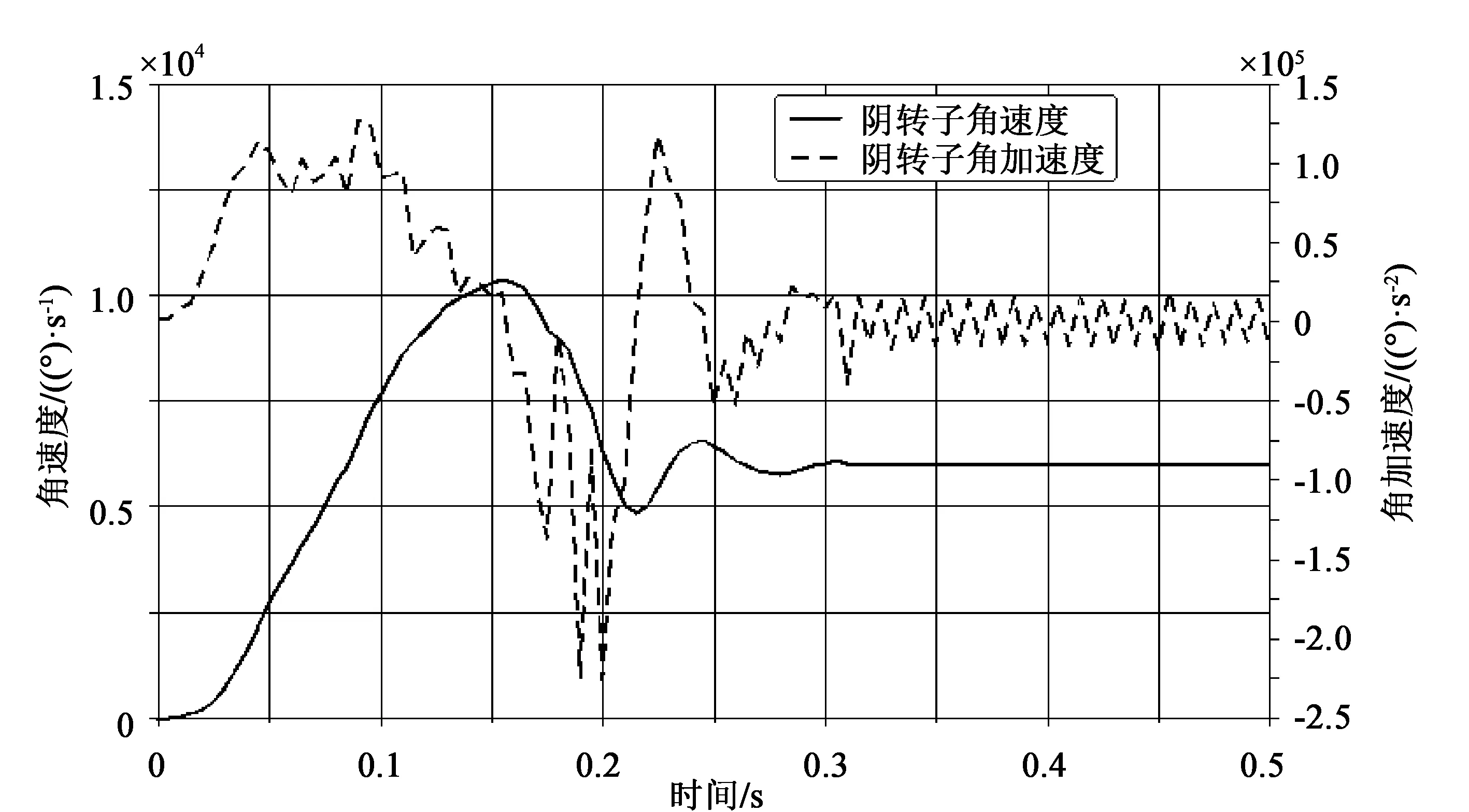
图5 0.5 s内阴转子角速度、角加速度曲线
由图6啮合力的时域图可知,开始工作时阴、阳转子之间突然受力,有较大冲击,之后保持在平均啮合力值附近上下浮动。阴、阳转子之间的法向接触力[9-11]为
Fn=Kδ3/2,
(4)
式中K为刚度系数,δ为阴、阳转子形变量。
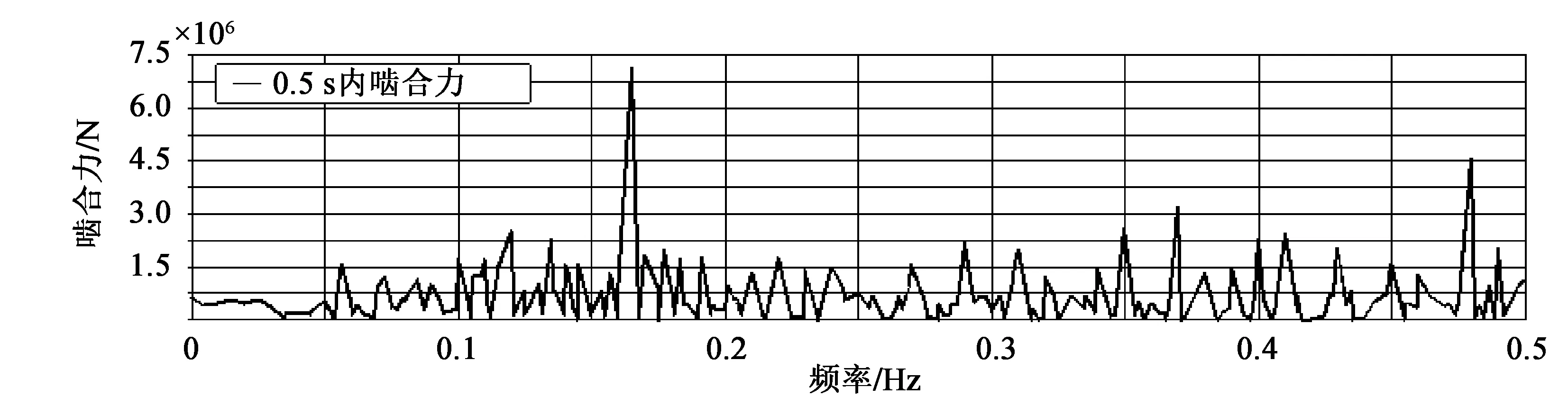
图6 啮合力时域图
由公式(4)计算法向接触力Fn为7.385 2×105N,与仿真平均啮合力值6.948 6×105N误差为5.91%,这是由于仿真中会有一定能量损失、仿真设置偏差、理论变形值不精确等等因素造成的,但阴、阳转子总体啮合传动还是比较稳定的。
4 结 语
本文根据齿轮啮合原理,在MATLAB中计算求得阴、阳转子端面截形,在SolidWorks中建立压缩机模型,通过ADAMS软件对螺杆压缩机虚拟样机进行运动学分析。在阳转子上施加了驱动转速,阴转子上施加负载转矩,得到了对应阴转子的速度、加速度和啮合力曲线,发现其满足螺杆压缩机运动条件,且通过对螺杆压缩机内部运动状况进行分析,可预先对其工作情况进行评估和优化,从而进一步改善压缩机性能。
