求“同”思“变——《圆》（整理与复习）课后练习

凌 佳

【教学内容】

人教版六年级上册第五单元课后练习。

【习题设计】

习题呈现（第一组题）

有一个半径为2 厘米的圆片。

解：最外边路线即为圆心经过的路程。

得出结论：圆心经过的路程=封闭图形周长+动圆周长。

【设计意图：本组习题设计从圆沿长方形滚动到沿正三角形和一般三角形等封闭图形滚动，将同一问题情境分成三种不同情况让学生经历解决问题的过程。当圆沿着正三角形滚动一周时，顶点处圆心经过的路线还是弧线，但所对的圆心角不再是90 度。此处设计沿正三角形滚动可以引发学生重新思考绕顶点滚动问题。当圆沿着一般三角形滚动时，因有先前的思考做铺垫，多数学生不难在对比和感悟中找寻到问题解决的策略，即“画出示意图，强化空间观念”，从而灵活地应对不同情况下的同一个问题。】

习题呈现（第二题组）

有一个圆片，半径为2 厘米。

解：外面的区域即为圆滚动一周扫过的面积。

得出结论：圆扫过的面积=封闭图形周长×圆直径+圆面积（以动圆直径为半径的圆）或圆扫过的面积=圆心经过的路程×动圆直径。

【设计意图：让学生先经历大胆猜想圆扫过的面积可能与什么有关，接着直观感受用实物圆在封闭图形外滚动一周，最后尝试动手画出示意图，从而验证自己的猜想。在知识形成的过程中培养了学生思维的深刻性。】

习题呈现（第三题组）

在长12cm、宽10cm 的长方形内，一个半径为2cm 的圆，沿这个长方形内壁无滑动地滚动一周。如图所示：

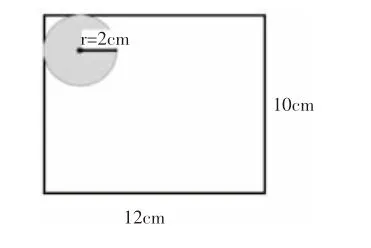
①求圆心经过的路程是多少？

②圆扫过的面积又是多少呢？

解①：图中里面长方形的周长即为圆在长方形里面滚动时圆心经过的路程。

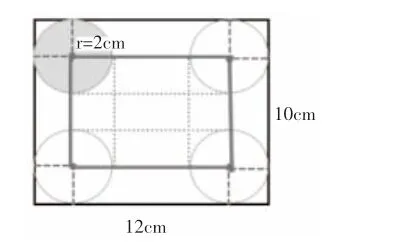
得出结论：圆在长方形内滚动时，圆心经过的路程=长方形周长-圆直径×4。

解②：如下图。

得出结论：圆扫过的面积=大长方形面积-小长方形面积-内圆外方相差部分面积。

【设计意图：通过对比，让学生感知圆在长方形外滚动时既有沿着直线滚动又有绕着顶点滚动，而圆在长方形里面滚动时只有沿着直线滚动的情况，引导学生从不同视角思考同一问题。】

【习题设计分析】

本习题适合放在《圆》（整理与复习）课后使用。通过变式题，将圆在不同封闭图形外滚动时圆心经过的路程的计算方法进行统一。通过对比圆在长方形外滚动和圆在长方形内滚动这两种不同情况，提炼圆在长方形内滚动时圆心经过路线和圆扫过面积的计算方法。习题功能在于，一方面考查学生对周长和面积意义的理解，帮助学生巩固圆周长及面积的计算方法；另一方面，通过图形形状变化与解决策略不变的思辨，以及图形形状不变而圆的位置改变，引导学生沟通圆在不同平面图形外滚动时的内在联系，体会圆在同一个图形内外滚动时的本质区别。

【设计感悟反思】

数学习题教学，不仅要整体把握知识本身，更要深度挖掘习题教学过程中的生长点。本习题设计以圆滚动过程中圆心经过的路程和圆扫过的面积为主线，通过封闭图形由长方形、正三角形到一般三角形的不断变化以及圆在同一个图形内、外滚动情况的不同，引导学生静下心来解读习题，理解设计中每个习题的编排意图，感悟每个习题的作用和目标，真正走进习题教学。本组习题将教学的着力点放在“抓住知识‘生长点’，激活数学思维”上。

1.抓住知识“生长点”，培养合情推理能力。

合情推理是从已有的事实出发，凭借经验和直觉，通过归纳和类比等方法推断某些结论。

例如，学生在探究“沿长方形外滚动一周，圆心经过的路程”时，根据圆沿直线滚动的经验发现：圆沿长方形贴边滚时，圆心经过的路线是直线。但是，圆绕顶点滚动时圆心的路线还是直线吗？此处即为学生的易错点。抓住学生的易错点，引导学生把“圆绕顶点滚动时圆心经过的路线”问题转化成“以封闭图形顶点为定点，到该定点距离为动圆半径的路线”问题，有利于学生猜想圆心经过的路线。根据“以定点为圆心，定长为半径”的作圆方法，学生合情推理出圆绕顶点滚动时圆心经过路线必定是圆周长的一部分。

2.抓住知识“生长点”，丰富空间观念。

在习题教学中，教师应该善于发现学生认知的“学困点”和“易错点”。设计有效的提问，促进学生思考，采用画示意图的方式，丰富学生的空间观念。

例如，教学“圆沿着长方形外滚动”这一习题时，让学生思考“圆绕长方形四个顶点旋转时圆心经过的路线为什么刚好围成一个圆”，引导学生尝试画出绕其中一个顶点旋转时圆心经过的路线示意图。通过画示意图的方式，我们发现贴边滚结束后经过顶点的直径与长方形的长垂直，绕顶点旋转后该直径又与长方形的宽垂直，绕一个顶点旋转了90°，四个顶点即360°，所以刚好围成一个圆。有效抓住了知识的生长点，让学生知其然，更知其所以然。

3.抓住知识“生长点”，提升概括能力。

有了圆在长方形外滚动的经验，探究圆在长方形里面滚动时，学生容易产生圆心经过的路线也是由直线和曲线组成以及圆扫过的面积只与封闭图形面积和动圆面积有关的认识偏差。通过相互辩驳，明晰学生的易错点，将学生思维引向深入，在对比、体验和感悟过程中，提升了学生的概括能力。

深度挖掘，让学生在有层次的练习中有所思有所悟有所得；整体把握，激活数学思维的同时也能让枯燥无味的数学知识自然生长。