基于变分模态和奇异值分解的柴油机气门间隙故障诊断方法研究*

高清春 胡甫才*

(武汉理工大学高性能船舶技术教育部重点实验室1) 武汉 430063)(武汉理工大学能源与动力工程学院2) 武汉 430063)

0 引 言

气门是柴油机的主要零部件之一，在柴油机工作过程中，气门会受到反复的落座冲击和振动影响，从而会使得进排气门间隙发生变化，出现故障，严重情况下甚至会妨碍柴油机安全可靠地运行，因此，对柴油机进排气间隙故障进行诊断非常重要[1-2].

最开始对柴油机进排气门间隙故障进行诊断的方法主要是基于小波包分析[3]和基于时频谱图的方法[4]，然而小波包分析方法对故障进行诊断时受选取小波类型的影响，选取的小波类型不同会使得故障诊断结果出现较大的误差，时频谱图方法通常不能实现故障的在线监测诊断.后来，学者们开始研究基于局部均值分解的方法[5]、基于经验模态分解和神经网络的方法[6]、基于经验模态分解和模糊聚类的方法[7]等，这些方法的本质是首先采用局部均值分解方法或经验模态分解方法对缸盖振动信号进行分解，然后再结合神经网络或模糊聚类方法对故障进行识别，然而局部均值分解方法和经验模态分解方法在对非线性非平稳的缸盖振动信号进行分解时存在端点效应和模态混叠等不足，会导致信号分解结果不准确，从而影响后面故障诊断识别的精度.

为了提高信号分解的准确度，克服局部均值分解方法和经验模态分解方法在信号分解过程中存在的端点效应和模态混叠等问题，Dragomiretskiy等[8]提出了变分模态分解(variational mode decomposition, VMD)方法，该方法能够对非线性非平稳信号进行自适应分解，能够得到更精确的分解结果，获得更精确的局部特征信息.

首先对缸盖振动信号进行VMD分解得到各个变分模态分量，然后对其进行奇异值分解(singular value decomposition, SVD)提取特征向量，最后用模糊C均值聚类方法对进排气门间隙故障进行诊断，同时，将提出的方法与基于EMD和SVD的故障诊断方法进行对比分析，并采用分类系数、平均模糊熵、欧几里得贴近度以及平均贴近度四种评价指标对故障诊断效果进行评估，研究提出的方法对柴油机进排气门间隙故障进行诊断的效果.

1 理论基础

1.1 变分模态分解

变分模态分解是Dragomiretskiy和Zosso提出的一种对信号进行分解的方法，具有坚实的理论基础，该方法在故障诊断和信号降噪等许多方面具有广泛的应用[9-11].

假设一个信号通过变分模态分解方法分解后得到K个变分模态分量，则其相应的约束变分问题为

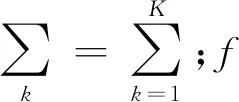
引入二次惩罚因子α和拉格朗日乘法算子λ将该约束问题转变为无约束的问题，得到扩展的拉格朗日表达式为

L({uk},{ωk},λ)=

(2)

式中：λ为拉格朗日乘法算子；α为二次惩罚因子；uk(t)为第k个变分模态分量.

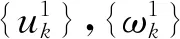
步骤2n=n+1.

步骤3对于k=1,2,…,K，执行

(3)

(5)

式中：τ为噪声容限参数.

步骤4判断是否达到收敛条件

(6)

式中：c为迭代停止阈值，这里设置为10-7.

如果达到收敛条件，则停止程序，否则继续执行步骤2.

通过执行上面的步骤后，能够得到各个变分模态分量信号.

1.2 奇异值分解

奇异值分解作为线性代数中的一种重要矩阵分解，在统计分析和信号处理等领域具有非常广泛地应用[12].

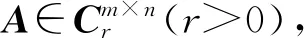
(7)

式中：Σ=diag(σ1,σ2,…,σr)为非零奇异值.

式(7)可写成矩阵A的奇异值分解形式，即

(8)

1.3 模糊C均值聚类算法

模糊C均值聚类算法[13]是将数据集x={x1,x2,…,xn}分为c类(2≤c≤n)，定义样本点xi属于第j(1≤j≤c)类的程度为隶属度uij(0≤uij≤1)，则与所有样本点对应的隶属度可构成隶属度矩阵，用U={uij}表示.

模糊C均值聚类算法就是求目标函数J(U,C)的最小值，J(U,C)定义为

(9)

式中：m为模糊加权数；cj为c类中第j类的中心；dij(xi,cj)=‖xi-cj‖为样本点xi与聚类中心cj之间的欧氏距离.

模糊C均值聚类算法采用迭代方法最小化J，其计算步骤为

步骤1确定聚类类别数c、模糊加权数m、迭代停止阈值ε以及最大迭代次数kmax，设置迭代次数k的初始值为1，根据以上约束条件初始化隶属度矩阵U(k).

步骤2由矩阵计算c个聚类的聚类中心cj.

(10)

步骤3由聚类中心cj更新隶属度矩阵U(k+1).

(11)

步骤4判断是否达到迭代停止条件

‖U(k+1)-U(k)‖<ε

(12)

如果达到，则停止迭代计算，否则令k=k+1，继续执行步骤2.

最后得到最终的隶属度矩阵U={uij}和聚类中心C={cj}.

1.4 计算流程

基于VMD和SVD方法的计算流程见图1.

图1 基于VMD和SVD方法的计算流程

通过试验测得柴油机缸盖振动信号，首先用VMD方法对其进行分解，得到各个变分模态分量，然后将各个变分模态分量组合成一个矩阵，用SVD方法提取特征向量，最后用模糊C均值聚类方法对柴油机的进排气门间隙故障进行诊断识别.

2 试验研究

试验对象为4120SG型柴油机，该柴油机为四缸四冲程水冷直列式柴油机，发火顺序为1—3—4—2.在试验过程中用CA-YD-182型加速度计测量4号缸缸盖表面进气门处加速度信号，用KISTLER 7613C缸压传感器测量缸压信号，用SM-12-100型磁电式传感器测量上止点信号，采样频率为50 kHz，用上止点信号截取柴油机一个工作循环的振动信号进行分析.

在试验中，通过调整改变4号缸进气门和排气门间隙，设置进排气门间隙异常故障.4号缸进气门和排气门的正常间隙为0.25与0.3 mm，在试验中设置了四组故障：进气门间隙0.4 mm、进气门间隙0.6 mm、排气门间隙0.5 mm、排气门间隙0.7 mm，在柴油机1 500 r/min空载工况下，分别测量进排气门间隙正常和异常状态下的4号缸缸盖表面进气阀处加速度信号.通过试验测得柴油机在正常状态下一个工作循环的缸盖振动信号见图2.

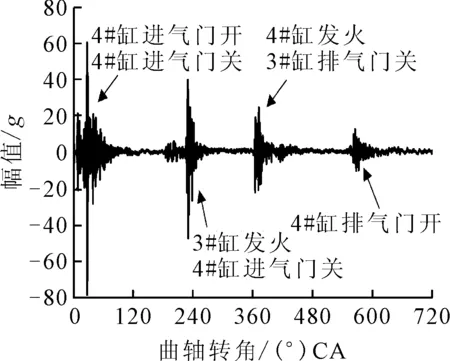
图2 缸盖振动信号

由图2可知，在0～90 (°)CA柴油机4号缸进气门关闭排气门开启，引起了缸盖振动信号的冲击响应；在170～270 (°)CA柴油机3号缸发火燃烧及4号缸进气门关闭引起了缸盖振动信号的冲击响应；350～450 (°)CA的缸盖振动信号冲击响应由4号缸发火燃烧和3号缸排气门关闭引起；540～640 (°)CA的缸盖振动信号冲击响应由4号缸排气门开启引起.

当4号缸进气门间隙为0.4和0.6 mm时，由于进气门间隙比正常进气门间隙0.25 mm增大，在进气门关闭时会对缸盖振动信号造成更大的冲击响应，在缸盖振动信号时域波形上表现为在相应曲轴转角范围内的振动信号幅值增大，但是直接从缸盖振动信号时域波形上很难直接判断出进气门间隙异常故障，尤其是准确地判断出进气门间隙相对正常状态下的增大幅度；同样的，对于排气门间隙异常及相对正常状态下的增大幅度情况也很难直接从振动信号时域波形上进行准确地判断，为此，下面基于VMD和SVD方法对进气门间隙异常和排气门间隙异常故障进行分析研究.

3 计算结果分析和讨论

对于测量得到的4号缸缸盖表面振动信号，首先用VMD方法对其进行时间序列分解，在用VMD方法分解缸盖振动信号时，需要事先确定分解得到的变分模态分量数目，这里通过依次观察对比各个变分模态数目所对应的中心频率来确定最优的变分模态分量数目，通过计算得到的结果见表1.

表1 模态数目K及其中心频率

表1为各个变分模态分量数目及各个变分模态分量的中心频率，对于缸盖振动信号而言，当两个变分模态分量的中心频率在1 000 Hz以内时，可以认为出现了过分解，显然，当变分模态分量数目为7时，有两个变分模态分量的中心频率分别为8 148和8 967 Hz，频率间隔在1 000 Hz以内，出现了过分解情况，因此，这里取变分模态分量的数目为六个.

用VMD方法将缸盖振动信号分解为六个变分模态分量后，将这六个变分模态分量组合成矩阵，用SVD方法提取特征向量.对于柴油机4号缸进排气门间隙正常(进气门间隙0.25 mm和排气门间隙0.3 mm)、进气门间隙异常(进气门间隙0.4,0.6 mm)、排气门间隙异常(排气门间隙0.5,0.7 mm)状态，对每种状态取五组试验数据分别用变分模态分解和奇异值分解相结合的方法提取特征向量，见表2.

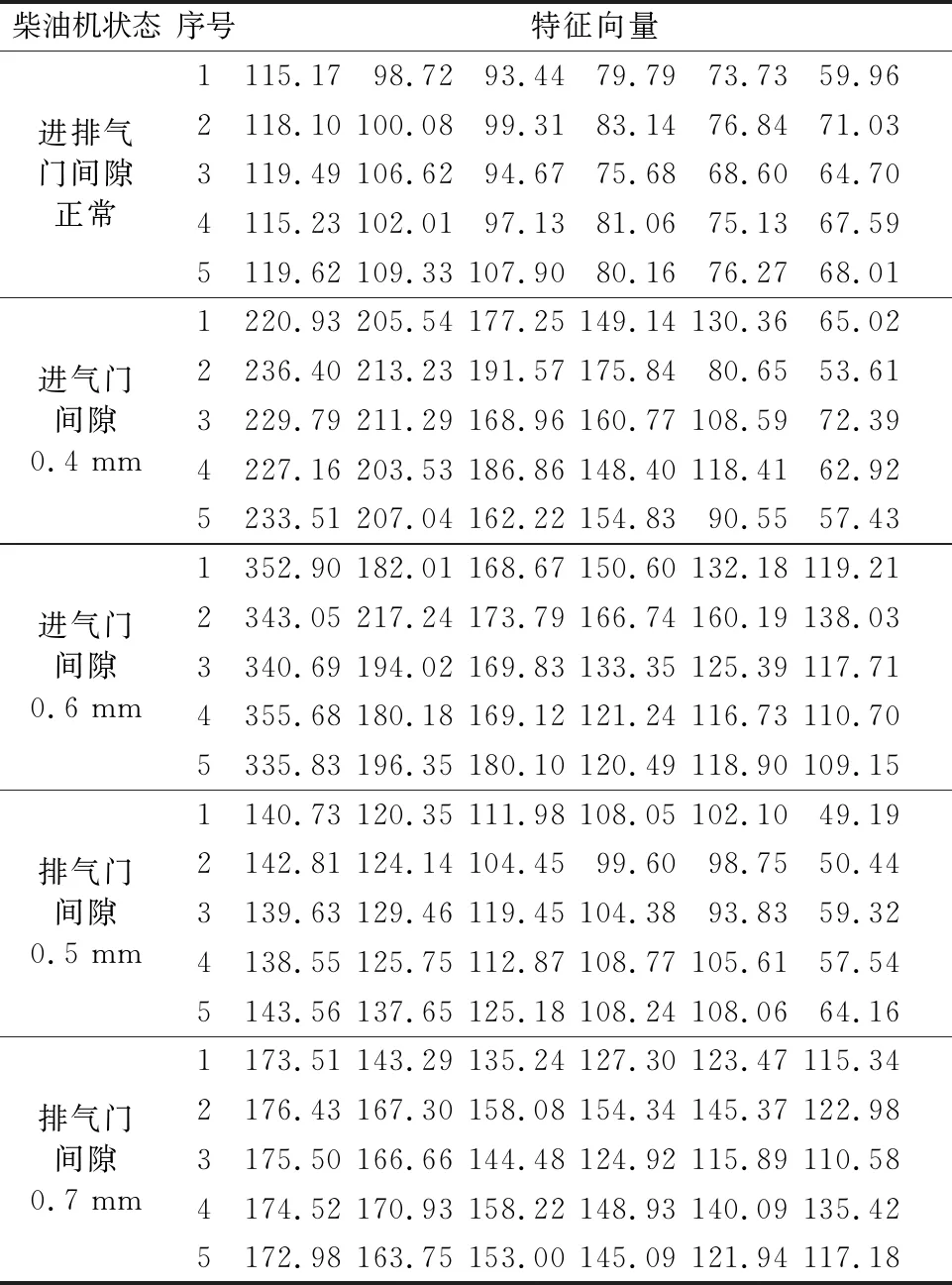
表2 特征向量

对于计算得到的特征向量，用模糊C均值聚类方法得到聚类中心矩阵C为

对每种状态另外任取2组试验数据样本进行分析，计算试验数据样本T和不同气门间隙状态聚类中心C的欧几里得贴近度，其计算公式为

通过计算得到的结果见表3.

表3 基于VMD和SVD方法计算结果

由表3可知，序号1和2表示选取的两组进排气门正常状态下的测试数据，其与正常状态所对应的欧几里得贴近度分别为-6.08和-3.28，贴近度最大，这表明这两组测试数据来自进排气门正常状态，与实际试验情况相符合；同样的，序号3和4表示选取的两组进气门间隙为0.4 mm的测试数据，序号5和6表示选取的两组进气门间隙为0.6 mm的测试数据，序号7和8表示选取的两组排气门间隙为0.5 mm的测试数据，序号9和10表示选取的两组排气门间隙为0.7 mm的测试数据，欧几里得贴近度最大值所对应的状态都与实际试验情况相符.通常情况下，当某一状态与其他状态的欧几里得贴近度的大小相差20时，能够明显地识别判断出某一状态，上面计算得到的结果都满足这一情况，因此，基于VMD和SVD方法能够准确地识别柴油机的进排气门间隙异常故障.

下面用经验模态分解(EMD)和SVD相结合的方法对柴油机进排气门间隙异常状态进行判断，首先用EMD方法对缸盖振动信号进行分解，可得到11个经验模态分量，然后计算各个经验模态分量与缸盖振动信号的相关系数，当相关系数小于0.1时，说明得到的经验模态分量与缸盖振动信号几乎不相关，这里选取相关系数大于0.1的四个经验模态分量，将这四个经验模态分量组合成矩阵用SVD方法提取特征向量，总共选取五组试验数据样本，并用模糊C均值聚类方法计算其聚类中心，然后再任取另外两组试验数据样本计算其欧几里得贴近度，计算结果见表4.

由表4可知，序号6(进气门间隙0.6 mm)的测试数据与进气门间隙0.6 mm所对应的聚类中心的欧几里得贴近度最大，为-10.71，然而其与另外一种状态(排气门间隙0.7 mm)所对应的聚类中心的欧几里得贴近度为-11.50，-10.71与-11.5相距较小，因此其故障识别效果不太好；同样的，序号8(排气门间隙0.5 mm)的测试数据与排气门间隙0.5 mm所对应的聚类中心的欧几里得贴近度最大，为-25.19，然而其与另外一种状态(排气门间隙0.7 mm)所对应的聚类中心的欧几里得贴近度为-27.92，-25.19与-27.92相距也较小；序号10(排气门间隙0.7 mm)的测试数据与排气门间隙0.7 mm所对应的聚类中心的欧几里得贴近度最大，为-25.52，然而其与另外一种状态(排气门间隙0.5 mm)所对应的聚类中心的欧几里得贴近度为-26.86，-25.52与-26.86相距也较小，因此其故障识别效果不太好.

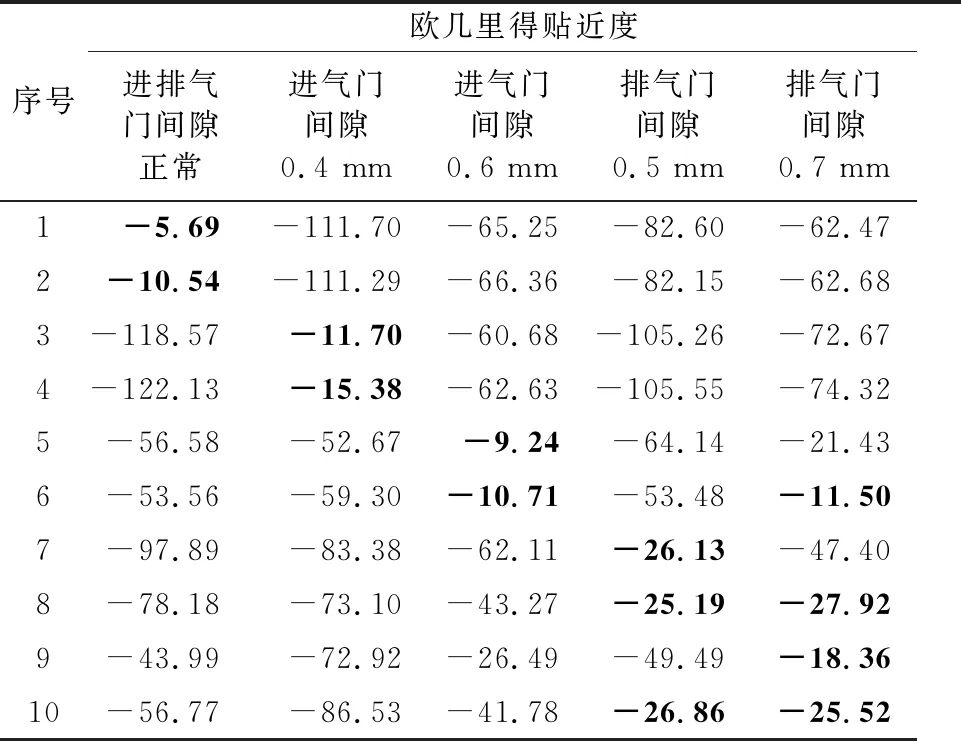
表4 基于EMD和SVD方法计算结果

对于模糊C均值聚类算法的分类性能，通常用分类系数F和平均模糊熵E来表示，其计算结果见表5.

表5 分类系数F和平均模糊熵E

分类系数F越大、平均模糊熵E越小则表示分类性能越好，由表5可知，VMD-SVD方法的分类系数F比EMD-SVD大，且平均模糊熵E比EMD-SVD小，因此，VMD-SVD方法的分类性能优于EMD-SVD方法.

为进一步分析VMD-SVD方法对柴油机气门间隙异常故障诊断的有效性，计算不同进排气门间隙状态的测试数据相对标准聚类中心的平均贴近度，计算结果见图3.

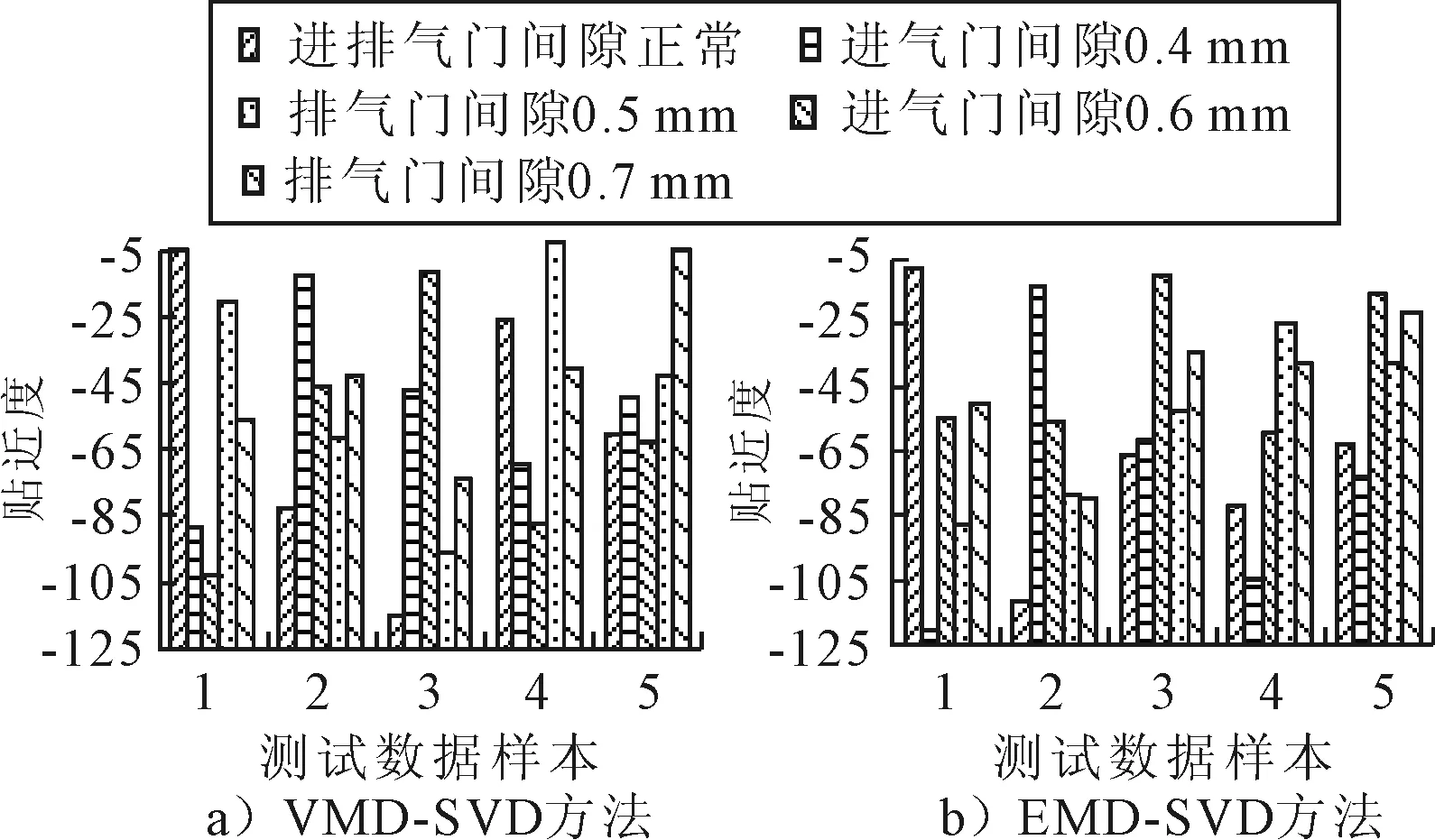
图3 平均贴近度

由图3可知，基于VMD-SVD方法的测试数据样本与标准聚类中心的平均贴进度整体上要大于基于EMD-SVD方法的平均贴进度，另外，由图3b)中方框可知，基于EMD-SVD方法计算得到的平均贴近度出现相距很近的情况，识别效果不好.

理论上，EMD算法的递归分解模式会使得上下包络线估计误差不断传播和扩大，导致分解得到的各分量信号不准确，易出现模态混叠情况，而VMD算法的非递归分解模式能够对分解得到的分量信号进行反向误差校正，能够更精确地对信号进行分解，因此VMD-SVD方法对柴油机气门间隙异常故障的诊断效果会优于EMD-SVD方法.

4 结 论

1) 用VMD-SVD方法和EMD-SVD方法分别对柴油机进排气门间隙故障进行诊断，并采用分类系数、平均模糊熵、欧几里得贴近度及平均贴近度四种评价指标对故障诊断效果进行评估，研究结果表明VMD-SVD方法相对EMD-SVD方法而言具有更高的诊断识别精度，能够更加精确地识别出进排气门间隙异常大小的程度，诊断效果更好.

2) VMD方法能够很好地对非线性非平稳信号进行分解，相对EMD方法而言具有更高的分解准确度，能够获得更多的局部特征信息，从而使得VMD-SVD方法能够更好地诊断气门间隙故障，同时也为柴油机的其他故障诊断提供了一种新的手段.

3) 本文只研究了柴油机单一的气门间隙故障诊断方法，没有考虑柴油机同时发生多种故障的情况，如同时发生气门间隙异常和气门漏气故障等，因此，下一步可开展柴油机并发故障的诊断识别方法研究.