考虑目的地选择的交通流分配双层规划模型及算法*

何胜学

(上海理工大学管理学院 上海 200093)

0 引 言

选择出行目的地和具体出行路线是交通出行的两个基本决策，也是进行交通网络系统运行效率评价和交通系统规划的重要组成部分.传统的交通规划四步骤法将上述两个决策按序分别考虑，忽视了两个决策间存在的相互影响.因此有研究者针对上述问题试图将两个决策问题整合为一个单层优化模型，但是在尝试构建这些单层组合模型过程中出现的特殊参数标定与不合理概念使得这些模型很难应用于实际.针对上述问题，本文尝试建立相应的双层规划模型来合理反映两个决策的特征与差异，并设计有效算法求解上述双层规划模型.

Wardrop提出了出行路径选择两原则，即Wardrop第一原则(用户均衡)和Wardrop第二原则(系统最优).Beckman给出了用户均衡交通流分配优化模型，即有名的Beckman变换.Leblanc首次给出了求解用户均衡模型的实用有效Frank-Wolfe算法.近年来研究者开始应用投影动态理论对动态和拟动态的交通流分配问题进行建模分析[1-4].针对路段流量一般受限于路段通行能力的情况，研究者也提出了有边约束的交通流分配变分不等式模型[5-6].为了反映路段行程时间函数具有的两阶段特征，最近研究者开始利用非凸规划理论研究交通流的分配和网络演化问题[7-8].

交通流分配中的组合网络模型也是研究者关注的重点.大致可分为：运量分布与交通分配组合模型、方式分担与交通分配组合模型、运量分布/方式分担/交通分配组合模型[9].本文关注的运量分布与交通分配组合模型又可分为：单运量分布约束组合模型和双运量分布约束组合模型.现有运量分布约束组合模型多为单层模型.运量分布约束组合模型中均需设定目的地吸引力测度指标Ms，∀s∈D[10].令O和D分别为起点和终点集合.令μrs为起点r∈O与终点s∈D间最短的可行路径行程时间.运量分布约束组合模型通常依据μrs-Ms大小决策起讫点对间交通量.Ms的量纲需要与μrs一致，在实践中通常很难给出符合要求的合理值.为了方便后续求解，考虑终点需求函数的单运量分布约束组合模型和常见的双运量分布约束组合模型一般会基于熵最大化理论在目标函数中加入对应项.而该加入项的系数需要利用历史的起讫点对间完整交通需求量加以标定，而该信息在现实应用时一般很难取得的.考虑到上述问题，本文通过建立双层规划模型，免去对熵最大化理论加入项系数进行标定的工作，同时放松了对目的地吸引力测度指标Ms量纲的限制.在建立的新模型中，终点s作为出行目的地对出行者的吸引力系数标定将更加方便和符合实际.

本文主要的贡献包括：①建立了考虑目的地选择的交通流分配双层规划模型.上层模型拓展了目的地选择概念，可以适用于各种已有的目的地选择理论，如重力模型和熵最大化模型.②设计了求解上述双层规划的有效算法.通过将下层路径选择模型抽象为一个映射，并利用经典Frank-Wolfe法对其进行求解，从而可以更有效地对上层目的地选择模型设计求解方法.将针对下层模型的Frank-Wolfe法嵌入为上层模型设计的可行下降方向法中，最终实现双层规划模型的求解.

1 模型构建

1.1 参变量介绍

1.2 目的地选择假设

经典的网络交通流分配模型一般假设起讫点对间的交通需求qrs给定.而实际中，交通规划者往往通过交通出行调查只知道任意起点总的交通需求量qr.因此需要对出行者的目的地进行选择，使其满足如下的起点基本流量守恒条件.

(1)

一般而言出行者对出行目的地的选取不仅需要考虑出行的行程时间长短，也许考虑备选目的地的吸引力大小.这里的吸引力主要指备选目的地满足出行者出行目的的可能性.例如，对于出行者购物需求，如果目的地是一个商业购物中心，则具有较强的吸引力.用吸引力系数As的值表示目的地的吸引力大小.在后续分析中，假设As的值给定.

下面给出两种情况确定目的地选择比例wrs的方法.第一种情况下，假设wrs满足

(2)

式中：m为一给定正整数，一般取值1或2.当m等于2时，式(2)与出行分布中的重力模型相一致，即由确定起点出发的出行者中选择某终点为目的地的数量与该起讫点对间的行程时间平方成反比.

第二种情形源于熵最大化理论，假设wrs满足

wrs=Asexp(-μrs)/∑d∈D[Adexp(-μrd)] (3)

至于实际中应用哪种假设则需要根据具体情况进行估计选择.两种情况下，∑s∈Dwrs=1均成立.

如果有了目的地选择比例，起讫点对间的期望交通需求量为

(4)

如果μ为由所有μrs构成的列向量，可将wrs视为μ的函数，即wrs=wrs(μ).

1.3 下层路径选择行为模型

针对出行者的择路行为，对应的用户均衡模型(user equilibrium model，UEM)为

(5)

(6)

(7)

(8)

与经典用户均衡模型的唯一差别在于上述模型中起讫点对间的交通需求量是待定的.式(6)为连接指定起讫点对的可行路段上的路径交通流量之和等于该起讫点对间的交通需求量.式(7)为路径流量的非负约束.式(8)为一个隐含约束条件，表明指定路段流量等于所有途经该路段的路径流量之和.式(5)可理解为所有路段的流量逐步累计过程中单位流量行程时间的加和.

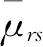
(9)

式中：上标“*”为相关量对应模型的最优解.

1.4 上层目的地选择模型

给定起讫点对间的交通需求模式q，由下层优化模型可以确定一个唯一的μ.上述关系可以抽象为映射μ=Ψ(q)或μrs=Ψrs(q)，∀rs.因此，wrs=wrs(μ)=wrs(Ψ(q))成立.

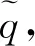
(10)

式中：q的可行集合定义为Q≡{q|qrs≥0,∀rs∈W;∑s∈Dqrs=qr,∀r}.

2 求解算法

下层模型(即抽象映射μ=Ψ(q)) 可利用Frank-Wolfe法进行求解，具体步骤为

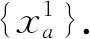
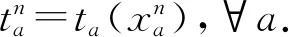
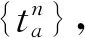
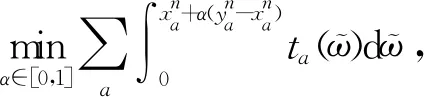
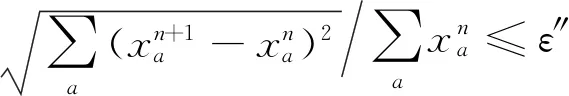
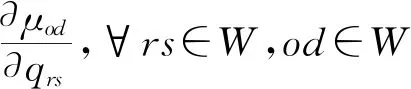
下面我们为式(10)设计一个可行下降方向法.由模型(10)的目标函数，可得

(11)

利用式(11)给出的dk可对q进行如下更新.

qk+1=qk+αkdk

(12)

具体步长αk的确定可以利用一维搜索算法实现.鉴于实现的复杂性，应当尽量减少调用下层求解算法的次数，因此可采用一些启发式一维搜索算法，如Armijo法.Armijo法中的步长αk=βmks，mk是从小到大满足下式的第一个非负整数：

以式(2)作为目的地选择比例的计算式，求解双层规划的具体步骤为

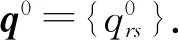
步骤2计算新的最短路行程时间.调用求解下层规划UEM的算法，计算得到μk=Ψ(qk).

步骤3方向搜索 按照式(11)，计算可行下降方向dk.

步骤4步长计算 利用Armijo法，依据式(13)计算得到αk.

步骤5交通需求模式更新.令qk+1=qk+αkdk.

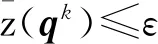
步骤6中的ε和ε′均为事先给定的较小正数，作为收敛指标.注意算法中目的地选择比例wrs的计算方法应保持一致，可以选择式(2)～(3)，也可以选择其他可能的形式.

3 算例分析

本节利用Nguyen和Dupius路网[11]来对本文提出的模型和算法加以验证.该路网包含13个节点，其中节点1和2为起点，3和4为终点.相关节点和路段的标号见图1.算法的终止指标设定为ε″=0.001、ε=0.05和ε′=0.05.上层模型算法中Armijo步长搜索的参数设定为σ=0.6、β=0.5和s=0.5.以式(2)中参数m为2时的重力模型来确定目的地选择比例.

图1 13个节点的Nguyen和Dupius路网

考虑两个不同的情景进行计算分析.情景1设定起点①和②的交通需求量分别为1 800和1 300，而终点③和④的吸引力系数分别为100和210.情景2设定起点①和②的交通需求量分别为1 800和2 300，而终点3和4的吸引力系数分别为200和120.

利用Java程序语言实现上节的算法，并在NetBeans IDE 8.0.2环境下执行.路段均衡流量的计算结果总结见表1；最终的交通需求分布结果见表2；计算过程中上层目标函数的变化记录见表3.两种情境下上层算法均执行七次后收敛，双层模型整体求解的运行时间均小于1 ms(即计算机显示执行时间为0，小于其可给出的最小时间单位1 ms).利用节点流量守恒条件可判定计算结果的合理性.

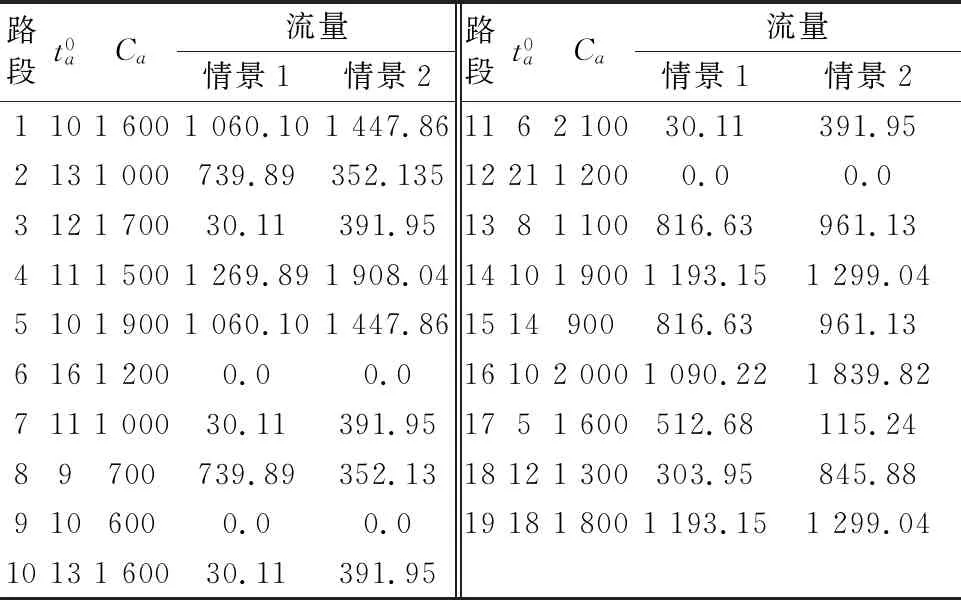
表1 路段行程时间函数的参数和均衡流量

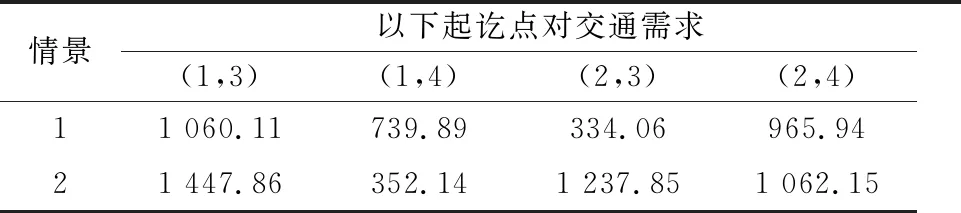
表2 交通需求分布结果

表3 上层目标函数变化情况

4 结 束 语

综合考虑出行目的地选取和路线选取两种决策，可以有效提高交通系统规划和系统运行评价的准确性和可靠性.本文通过设计整合两种决策的双层规划模型，不仅拓展了现有理论处理目的地选择模型的灵活性，也降低了现有模型应用时面临的参数标定工作.本文设计的内嵌经典用户均衡模型的Frank-Wolfe法的可行下降算法可以实现对本文双层规划模型的高效求解，因此其实际应用前景良好.