航天服硬式髋关节耦合机构建模与运动分析
2019-08-29王振伟徐利梅谢晓梅李学生林丹兰
王振伟,程 鹏,徐利梅,谢晓梅,李学生,林丹兰
(电子科技大学航空航天学院,成都611731)
1 引言
航天服是航天员的重要生命保障和支撑系统。星表作业要求航天服的关节系统具备较好的运动性和灵活性,以完成行走、维修、搬运等任务[1]。通常,航天服内维持一定的压力,服内压力会给航天服关节弯曲运动带来较大阻力,降低星表作业的效率。通常采用旋转轴承[2-3]、活动框架[4-5]和织物褶皱[4-6]等结构来提高关节的活动性能,如美国“水星”航天服、“双子星”航天服、MARK III、Z-1、Z-2,俄罗斯“海鹰”航天服,中国“飞天”航天服等。围绕航天服关节系统,目前在结构设计[7]、阻力/阻力矩分析[8]、动态性能计算[9]、人机交互性能[10]等方面开展了一系列研究。随着月球、火星、土星等星表探测的发展对航天服下肢关节系统提出了更高的要求。
目前,航天服下肢髋关节研究工作多数集中在制造加工、试验测试等方面。围绕航天服硬式髋关节的运动分析,本文提出一种3自由度混合机构模型,阐明大腿-髋关节耦合机构的运动原理,完成机构运动自由度分析,建立机构的运动方程。
2 髋关节的机构建模
2.1 髋关节机构的设计模型
本文基于航天服概念设计模型如图1所示。它是一种软硬复合式航天服,由软、硬两种类型关节构成,具体参见文献[11]。其中,硬质髋关节是本文的主要研究对象,其设计模型如图2所示。为满足大腿3自由度运动需求,提出由球冠形关节串联而成的髋关节概念设计方案。每个髋关节构件都以半球形薄壳体为基础,通过切削球体来获得具有一定斜面的球冠形壳体;各髋关节构件通过轴承依次首尾连接,组成可相对旋转运动的串联机构;在大腿运动过程中,每个髋关节构件围绕自身轴线旋转,从而改变髋关节构件的空间位姿,实现髋关节和大腿的同步运动。
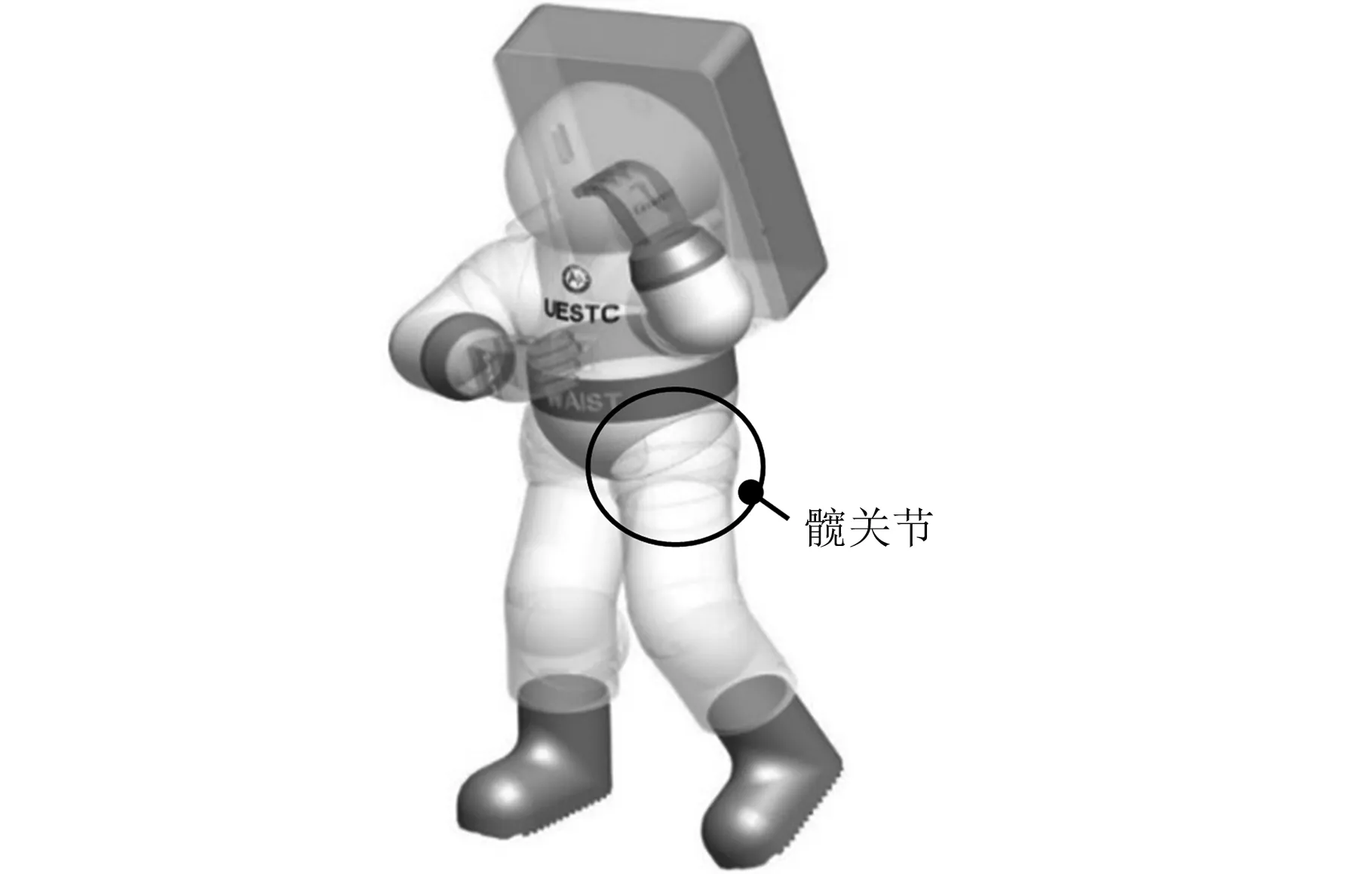
图1 航天服的概念设计模型Fig.1 Conceptual design model of spacesuit

图2 髋关节机构的设计模型Fig.2 The design model of hip joint mechanism
髋关节的设计参数包括球壳半径ri和倾角ai,如图3所示。由于各髋关节构件采用串联连接方式,当初始髋关节构件的半径r1由设计任务给定时,其它髋关节构件的半径ri+1可由相邻髋关节构件的半径ri和倾角ai计算获得,即ri+1=ri×cosai。因此,髋关节机构的设计参数主要是指各髋关节构件的倾角ai。同时,考虑到连接轴承的尺寸和体积相对较小,对髋关节机构的运动分析影响不大,因此忽略连接轴承的建模与表达。
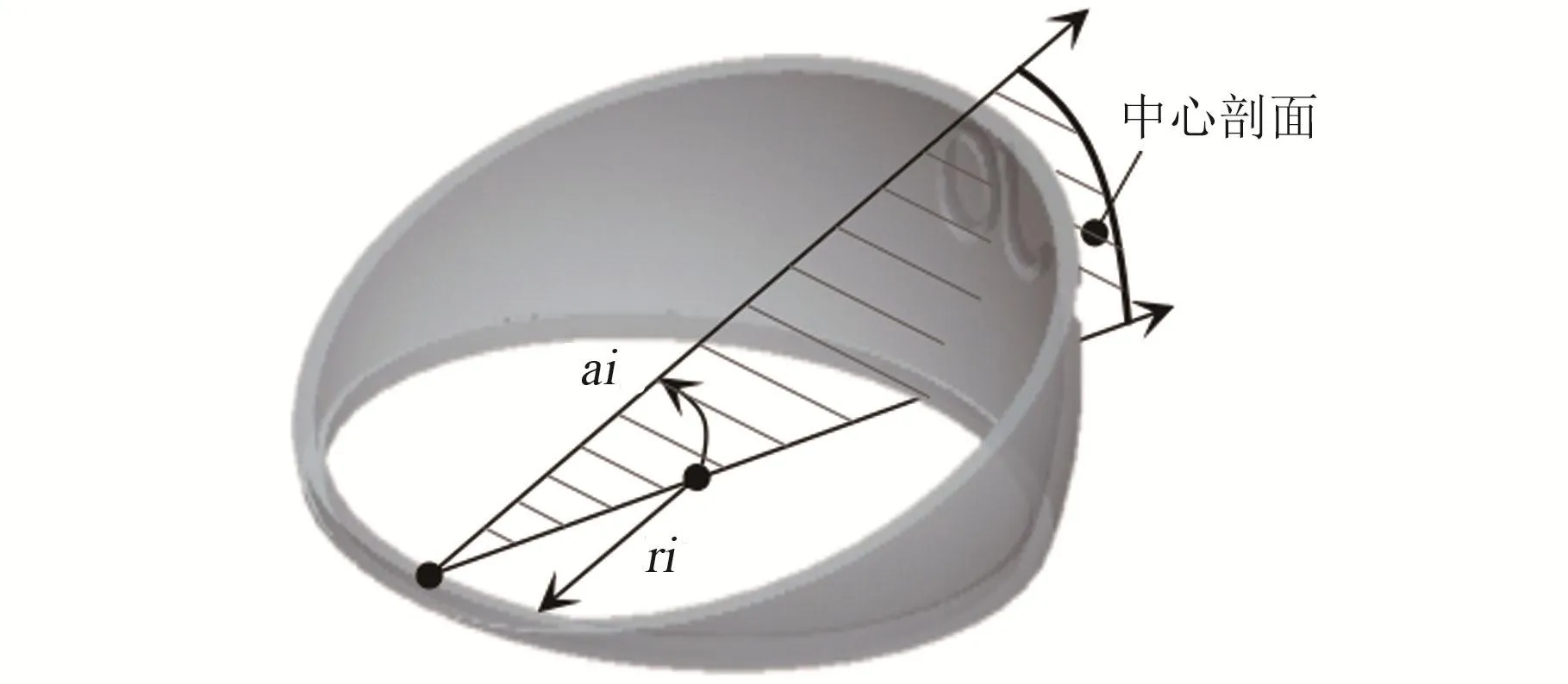
图3 髋关节构件的设计模型Fig.3 The design model of hip joint component
根据大腿的摆动要求建立髋关节机构的3个约束条件:
1)自由度约束。为了满足人体大腿的运动需求,建议航天服髋关节机构具备3个以上的自由度。为了运动分析的方便,避免运动解的不确定性,拟定髋关节具有3个自由度。
2)正交约束。在人体大腿摆动过程中,需要保证髋关节机构的“下连接面”始终与大腿中心轴线保持正交,以避免航天服下肢系统对人体大腿运动的干涉、阻碍和碰撞,甚至是损伤。
3)固定约束。通常,人体大腿关节点固定不动,它不随大腿摆动而改变位置。因此,要求航天服髋关节铰点具有位置保持性,机构设计时应明确给出人体大腿关节位置,并维持不变。
2.2 大腿-髋关节的机构模型
髋关节构件是关于中心剖面对称的球壳结构,将图3所示髋关节构件的设计模型进行抽象,在中心剖面上建立相应的髋关节构件数学模型如图4。具体而言,将髋关节构件简化为由上连接副和下连接副组成的连杆模型。其中,上连接副和下连接副分别位于髋关节构件的上/下连接面的转动中心处,它们都是转动副,是对连接轴承的简化且与对应端面保持正交。这样,髋关节构件数学模型的表达参数包括ai、di和ri。其中,di是髋关节构件的上/下连接面的圆心距离,或称为连杆的长度。在运动分析时,可用一个矢量表征。
目前研究大都只考虑髋关节构件的本体建模与计算,忽略了人体大腿和髋关节机构的相互耦合作用。为此建立大腿-髋关节耦合的机构原型,如图5所示。
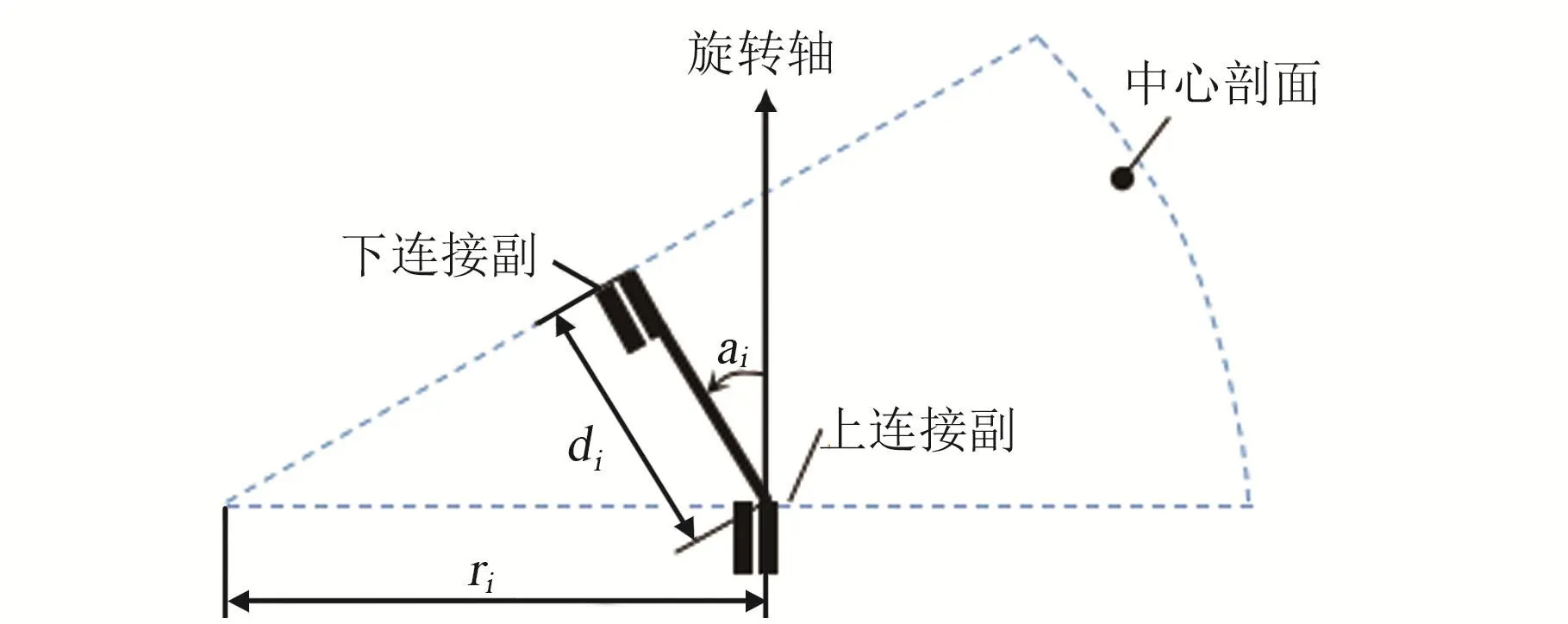
图4 髋关节构件的参数模型Fig.4 Parameter model of hip joint component

图5 大腿-髋关节耦合的机构原型Fig.5 Prototype of thigh-hip joint coupling mechanism
该机构原型包括4个旋转副、1个球面副、1个圆柱副、4个连杆和1个摆杆。其机构构型是一个串并混合的闭合式机构。其中,大腿简化为具有3个旋转自由度的摆杆,K点为大腿摆杆的关节铰点。大腿摆杆lKS与末端髋关节构件的下连接副采用了圆柱副连接,从而保证了髋关节机构与大腿轴线的正交约束条件。同时,将初始髋关节构件抽象为与机架的转动连接。
对于大腿-髋关节机构的自由度,由图5可见,大腿-髋关节机构包括5个构件,分别是连杆1、连杆2、连杆3、连杆4和摆杆,并具有4个转动副、1个圆柱副和1个球面副。初始髋关节构件虽然与航天服上身相连,但对大腿运动没有影响,因此将航天服上身看作是固定机架。在三维空间中,一个构件具有6个自由度。1个转动副提供5个约束,具有1个旋转自由度。1个圆柱副提供4个约束,具有1个旋转自由度和1个移动自由度。1个球面副提供3个移动约束,具有3个旋转自由度。对于图5机构而言,其自由度计算如下:5个构件共具有5×6=30个自由度,4个转动副共具有4×5=20个约束,1个圆柱副具有4个约束,1个球面副具有3个约束。因此,“大腿-髋关节机构”自由度为30-20-4-3=3。这与人体大腿的自由度数相同,满足髋关节机构的自由度约束条件。
2.3 机构模型的简化与确定
由图5可见,大腿摆杆lKS需要完成空间3自由度旋转运动。而且,要求转动过程中,铰点K的位置不发生变动,即固定约束。由几何关系可知,当大腿摆杆lKS位于空间中任意2个不同方位的时候,只有铰点K位于转动轴S1上,才能满足位置不变的固定要求。此外,为了进一步简化机构模型,缩小机构模型的体积和规模,考虑到连杆1的长度对机构自由度没有影响,令其长度为0,使得转动副1和转动副2重合,形成了复合转动副。同时,令铰点K与转动副1重合。最终建立的大腿-髋关节的机构模型如图6所示。

图6 大腿-髋关节耦合的机构模型Fig.6 Model of thigh-hip joint coupling mechanism
综上,大腿-髋关节机构模型满足了人体大腿摆动的3个自由度要求。
3 大腿-髋关节机构的运动分析
3.1 大腿-髋关节机构的运动分析
为了完成髋关节机构的最终设计,需要根据设计需求和运动要求,通过计算分析来确定该机构模型的具体参数,包括所有连杆长度、角度和大腿摆杆铰点K的位置。髋关节机构设计需求通常是给定的,包括相应髋关节构件的半径参数和摆动角度范围。令初始髋关节构件的半径为r1,末端髋关节构件的半径为r4,髋关节机构的摆动角度范围为[0ad]。而且,上述参数r1、r4和ad通常为已知量,由设计要求直接给出。同时,根据人体大腿的自由空间运动需求,要求大腿摆杆lKS可以正确地运动到空间中任意位置。从数学分析角度来讲,要求大腿摆杆lKS能够完整地表达任意给定的空间方位矢量。
从运动形式来看,大腿-髋关节机构运动形式是空间定点转动。为此,需要完成空间定点转动的运动分解。本文将大腿摆杆lKS的空间运动分解为两类转动运动。第一类转动运动是大腿摆杆lKS围绕关节铰点K的自由平面转动。该类平面转动可通过所有髋关节构件相对转动来合成,需要保证大腿摆杆lKS能够到达平面内的任意方位。第二类转动运动是大腿摆杆lKS围绕大腿-髋关节机构转动轴S1的定轴转动。该类运动需要一个旋转副,以保证大腿摆杆lKS自由地转动到空间任意方位。由上可见,第二类转动运动较为容易,可以由复合转动副来表征。下面主要讨论第一类转动运动。
根据机构模型建立大腿-髋关节机构的平面转动几何模型如图7。线段OA和AB分别表示连杆2和连杆3,线段OS表示大腿摆杆lKS。根据髋关节机构的运动原理,线段OA围绕y轴转动,线段OH是线段OA定轴转动的对称位置;线段AB围绕线段OA转动,线段AC是它定轴转动的对称位置,其中,为了保证大腿摆动的连续性,点C须位于y坐标轴上。点A和B运动轨迹的xz面投影分别为圆C2和圆C1。线段OS上任意点P投影为点F,点B投影为点E。过F点做围绕O点的圆C3,与圆C1相交于点Q。点Q是该状态下点P对应运动点P′的投影点,这里称点P′为影点。具体而言,当线段OS围绕点O从起始位置OB顺时针转动a角时,相当于线段AB上点B的投影点E由点E沿着圆C1顺时针转动到点Q。同时,点Q与线段OA同步围绕y轴沿着圆C3逆时针转动到点F。这样,通过线段AB和OA同步运动实现了线段OS的平面转动。此外,由图7可见点B和C是大腿摆杆的两个极限运动位置,也是机构运动的不确定点。因此,应该在这两个位置上设定必要的限位装置,以避免不确定状态的影响。
另外,线段AB和OA在线段OS转动过程中始终保持长度不变。因此,夹角∠APO为一个常数。这样,通过点B可做一个始终与线段OS正交的平面,其交点为T。由几何关系可知,相应夹角∠TBC=a3-a2。根据正交约束条件,该夹角等于末端髋关节构件4的设计倾角a4。综上,4个髋关节构件倾角设计参数中存在2个约束关系式:a1=0和a4=a3-a2。即当确定了a3和a2后,髋关节尺寸可以完整确定。
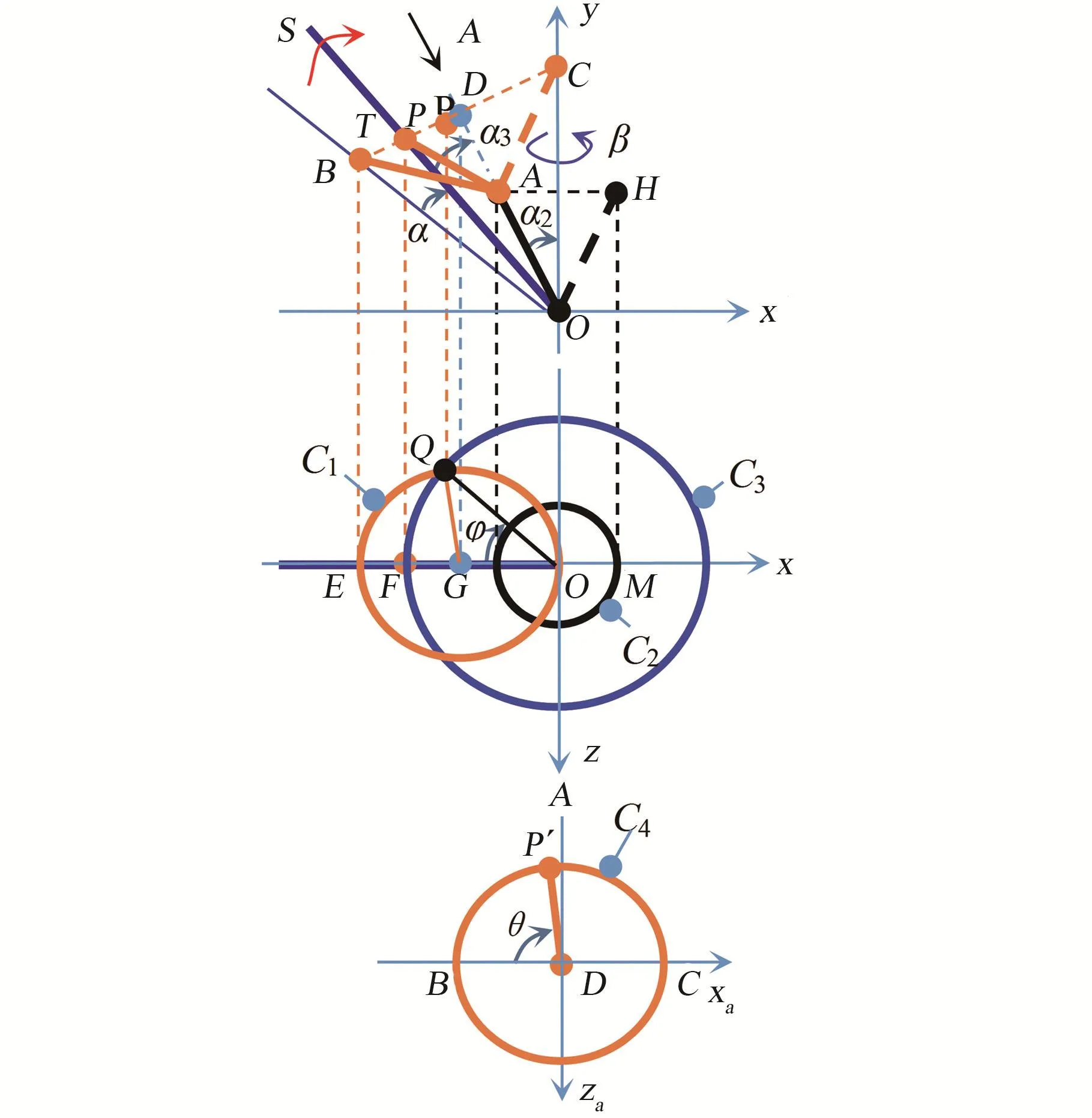
图7 大腿-髋关节机构的平面转动几何模型Fig.7 Planar rotational geometry model of the thighhip joint mechanism
3.2 大腿-髋关节机构的运动方程
设线段OB为线段OS的初始方位,由3.1节运动分析可知,当线段OS围绕点O转动α角时,线段AB的对应转角为θ,线段OA的对应转角为φ。其中,在A向视图内表达转角θ,在xz坐标面内表达转角φ。线段OA和AB的对应倾角为α2和α3。 当转角α在0~2α2范围内变化时,线段OS上点P在线段BC区间内移动,而且点P位置与转角α之间形成一一映射,因此,可建立点P位置矢量关于转角α的参数表达公式。在坐标系xyz中,设点B和C位置矢量分别为PB和PC,则点P位置矢量由公式(1)给出。
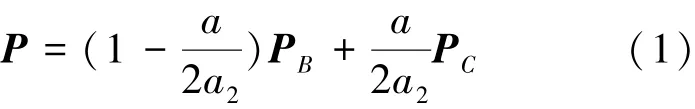
其中,

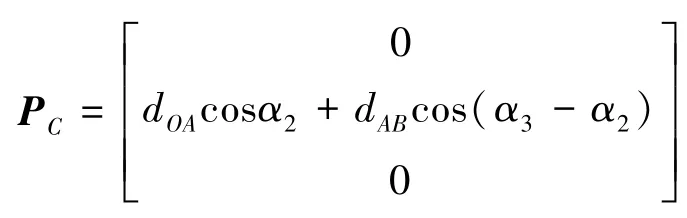
如前所述,影点P′在A向视图的运动轨迹为圆形C4,在坐标面xz内的投影点为Q。由图7可见,转角θ和φ与影点及其投影点Q直接相关。若能求得影点P′在坐标系xyz中的位置矢量P′a,则投影点Q的位置坐标便可确定,进而求解转角θ和φ。为了获得影点P′在坐标系xyz中的位置矢量,需要进行坐标系xayaza到坐标系xyz的坐标变换。设上述两个坐标系之间的变换矩阵为TC4-C1,根据坐标变换理论和矢量运算,可得影点P′在坐标系xyz中的位置矢量如式(2)。

其中,
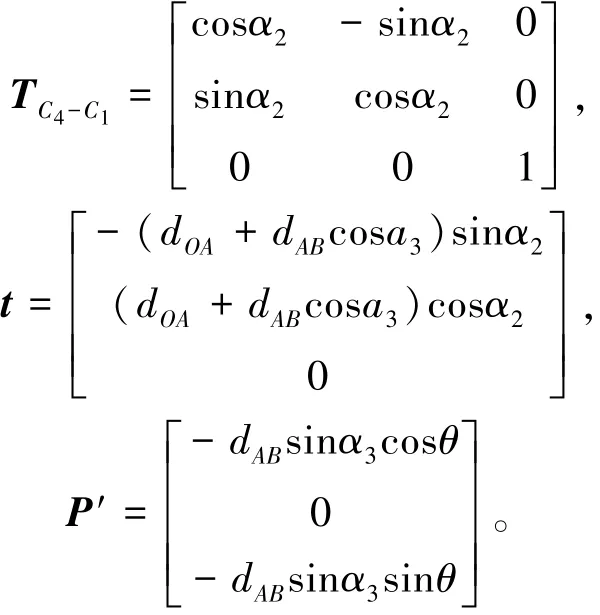
由图7可见,随着点P位置的不断变动,投影轨迹圆C3半径和点Q位置跟随变化,使得转角φ也在不断变化。但是,圆轨迹的形状不变,线段OQ和线段OF的长度相同。因此,点Q位置矢量长度就等于点P位置矢量的x坐标分量,从而得点Q位置矢量长度‖Q‖的计算公式(3)。

其中,是坐标轴x的单位向量。将点P位置矢量表达式(1)代入式(3),可得到点Q位置矢量长度‖Q‖的计算公式,如图(4)、(5)所示:
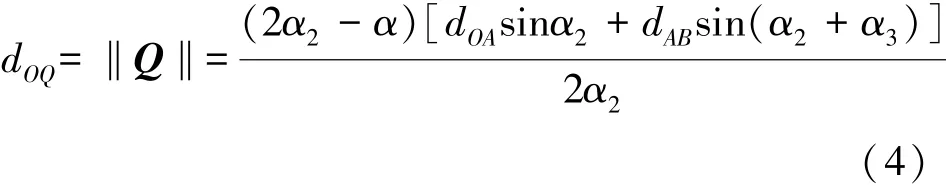
其中,

可得点Q位置坐标在坐标面xz内的表达式(6)。
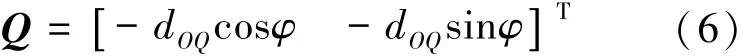
由于圆轨迹C1和圆C3在点Q处相交,因此,点Q位置矢量必将满足影点P′在坐标面xz内的投影方程。将式(6)带入式(2),可得式(7)。
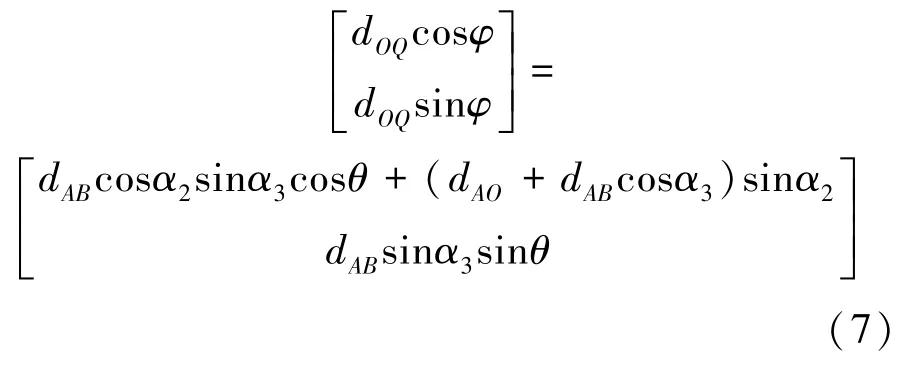
求解公式(7),可得转动角度φ和θ表达式(8)。

综上,完成了大腿-髋关节机构运动方程的建立。给定倾角α2和α3后,可得到任意转动角度α所对应的转角θ和φ值。由式(5)可见,给定r2,式(8)只与α2和α3有关。 但是,大腿-髋关节耦合机构模型还需要满足一定的几何约束。下面详细讨论式(8)的具体求解流程。
3.3 大腿-髋关节的运动约束方程
如前所述,式(8)从几何关系角度出发给出了运动方程,没有考虑几何要素之间的约束关系。由图7可见,本文所提出的大腿-髋关节耦合模型存在2个几何约束关系:第一个约束关系是点C的点线重合约束,3.1节已给出了“点C须位于坐标轴y上”的几何约束;第二个约束关系是4个髋关节构件之间的连接关系约束。这2个约束关系将进一步简化运动方程求解。下面,分别推导上述2个几何约束的表达公式。
由图7可见,要求点C始终位于坐标轴y上,以保证大腿摆杆(线段OS)运动空间的完整性。因此,在△OAC中,线段AC和线段OA之间始终满足正弦定理,且线段AB和线段AC的长度始终相等。经进一步计算可建立由线段AB和OA长度表达的点线重合约束式,并将其表达髋关节半径参数r2和倾角α2和α3的形式,如式(9)所示:

此外,由于各髋关节构件之间采用串联连接关系。因此,各髋关节构件的半径之间存在几何约束,具体见2.1节。根据图6中髋关节机构模型,初始髋关节构件的半径r1=0,因此,将髋关节构件半径尺寸r2作为初始设计值,并假设其为已知值。依据各髋关节构件的半径约束关系,将线段长度dAB表达为髋关节半径参数r2和倾角α2和α3的表达形式,如式(10)所示:
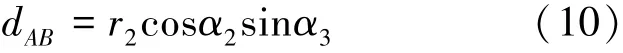
联立式(9)和(10),可得总的约束式(11)。
(sinα3)2-tanα2sinα3cosα3=(tanα2)2(11)
由式(11)可见,倾角a3和a2相关。当给定转角a2,角度a3也就确定。因此,大腿-髋关节机构是单约束完整系统。进一步求解公式(11),可得转角a3的计算公式(12)。
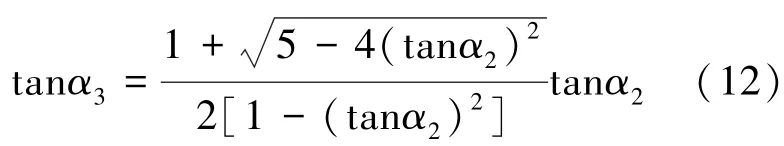
由式(12)可见,分母项不能为零,求得转角a2变化范围为0~45°。通常,机构设计任务书都给定大腿摆杆的运动范围极限角度ad。因此,转角a2和极限值ad之间存有一定约束关系。由图7中的线段之间几何关系,可得到极限角度ad的表达式,如式(13)所示:

综上,当给定设计参数r2和ad,按照图8计算流程图可得大腿-髋关节机构的运动方程。
3.4 仿真算例
进行髋关节转动角计算仿真时,通常转角θ1是自由转动变量,与机构尺寸无关。为计算方便,本算例令转角θ1=α3-α2。主要考察转角θ2和θ3的变化情况。 由图6和图7可见,θ3=-θ,θ2=-φ。由于上述各公式均为解析表达式,得到结果如图9和图10所示。 其中,令r2=226 mm,ad=88°。
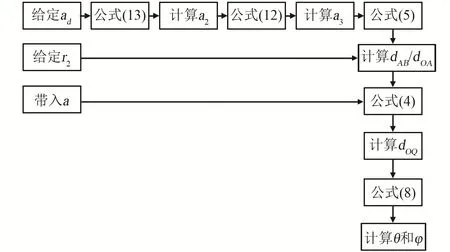
图8 计算流程Fig.8 Calculation process
由图可见,这两个运动角度曲线是连续的、有界的,符合下肢运动的范围要求和实际步态变化。因此,本文提出的耦合机构模型是合理的,运动分析方程是正确的。
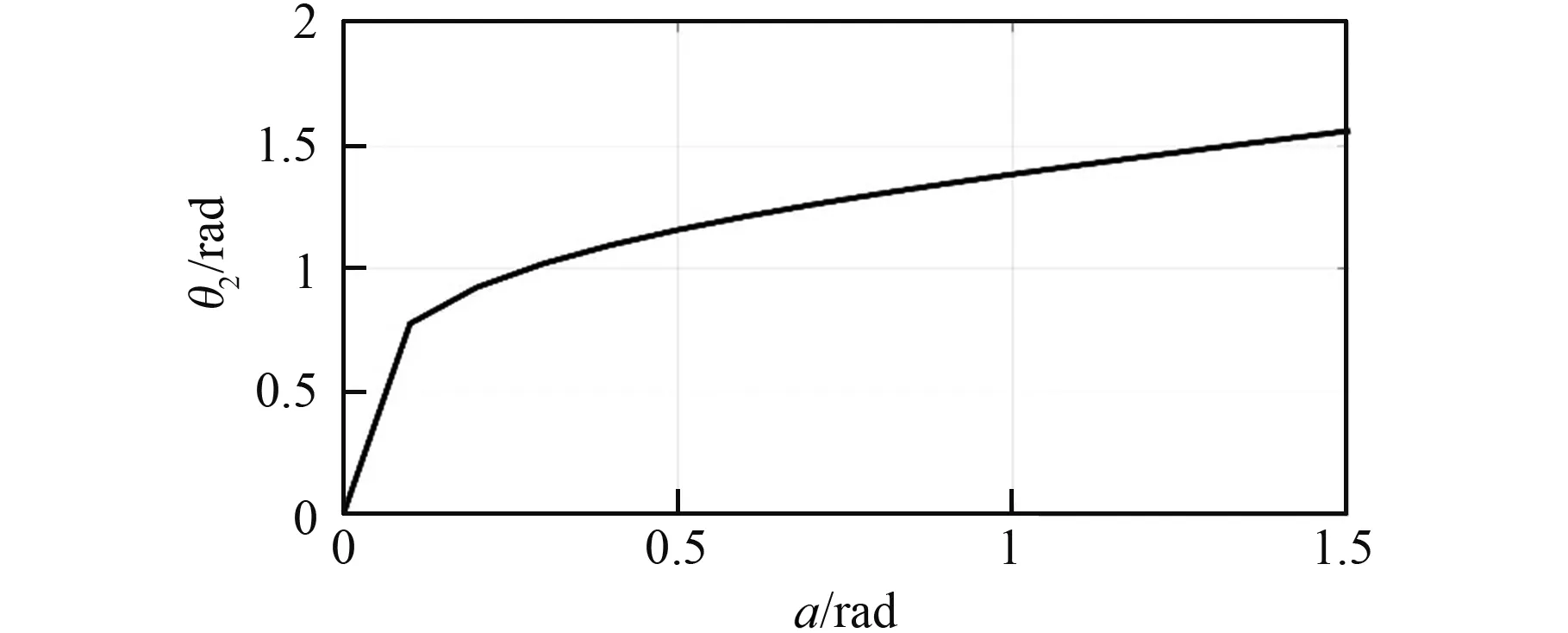
图9 转角θ2的变化曲线Fig.9 Curve of rotation angle θ2

图10 转角θ3的变化曲线Fig.10 Curve of rotation angle θ3
4 结论
1)从机构组成原理来讲,大腿-髋关节耦合机构是一种串联混合机构,且与人体大腿具有相同的自由度。
2)大腿-髋关节耦合模型有3个约束条件:3自由度约束、固定约束和正交约束。在上述约束条件下,大腿-耦合机构具有明确的机构构型和运动形式。
3)通过矢量表达方法所建立的机构运动方程与实际人体大腿的运动形式相一致。
4)大腿-髋关节耦合机构是一种参数化模型,可用于不同设计参数的髋关节运动分析,这为航天服硬质髋关节设计提供了一种较为通用的运动分析工具。
