采用主目标进化遗传算法的织造排程研究

2019-08-28潘如如高卫东王静安周利军

纺织学报 2019年8期

孟朔，潘如如，高卫东，王静安，周利军

(1. 生态纺织教育部重点实验室(江南大学)，江苏无锡 214122；2. 丹阳市丹盛纺织有限公司，江苏镇江 212309)

织造作为纺织企业生产的核心工序，决定了企业的生产效益，而目前个性化的产品需求使纺织企业存在订单多、批量小、品种杂、交期要求严格的问题。当前人工排程不仅会引起订单超期，品种翻改次数增多，还会增加计划工人的劳动强度，降低车间生产效率，因此，合理高效的计算机排程方法成为企业关注的焦点。Abedinnia等[1]总结了车间调度问题的相关智能算法。邹泽桦等[2]使用改进遗传算法来解决车间多目标调度问题，取得了较优效果。

尽管调度问题在各领域也都有研究应用，但在纺织领域并针对织造环节的研究仍较少。文献[3]提出使用简单遗传算法对织造问题进行建模求解，虽取得了一定成果，但对多个优化目标使用线性加权计算适应度，具有一定局限性，且未考虑织机约束。韩江洪等[4]采用的基于Petri网的建模方法理论严密，图形表达直观，但同样存在模型复杂，计算效率低的问题。EROGLU等[5]同时考虑了织机约束与订单分割，但当解决大规模织机调度问题时运算时间较长，且为单目标优化。

本文研究立足于工厂的实际生产，在现有研究的基础上从多目标与单目标转化角度出发，提出用主目标进化遗传算法来解决织造排程问题，并以某织造车间生产实例进行了仿真实验。

1 织造生产排程模型

1.1 问题描述

在企业，织造车间拥有多台不同类型的织机，其生产进度各不相同，需要对多个订单的多个小批量品种进行排程，以安排织造生产，提高企业效益。

已知某时刻下的织机、织造、品种与订单等信息，在企业实际排程中，通常以满足订单交期为主来尽量提高生产效益，主要体现在：提高织机利用率，减少空车数与品种翻改次数，并且当订单交期较长时尽可能使用较少的织机来完成生产以降低库存成本，便于安排其他订单；同时由于订单批量小，生产周期相对较短，一般不会调整其他订单完工时间来保证紧急单的生产。

基于企业实际排程需求，为简化计算复杂度，本文忽略人工、生产管理、紧急插单等，假设织轴的上机时间均为T，织机均服从经验数据进行生产。算法通过对订单分轴，满足织机可织品种约束，优化实现多个目标要求。另外，每当出现插单、停单、机台故障或者偏离实际计划较大时，算法会对所有未实际安排的订单重新排程，寻求更优计划来指导生产。

1.2 优化目标

织造企业调度计划的目标主要体现在按时交货、降低成本与提高织机利用率，结合企业实际需求，设立如下目标函数：

f1=max(T1,T2,···,Tm)

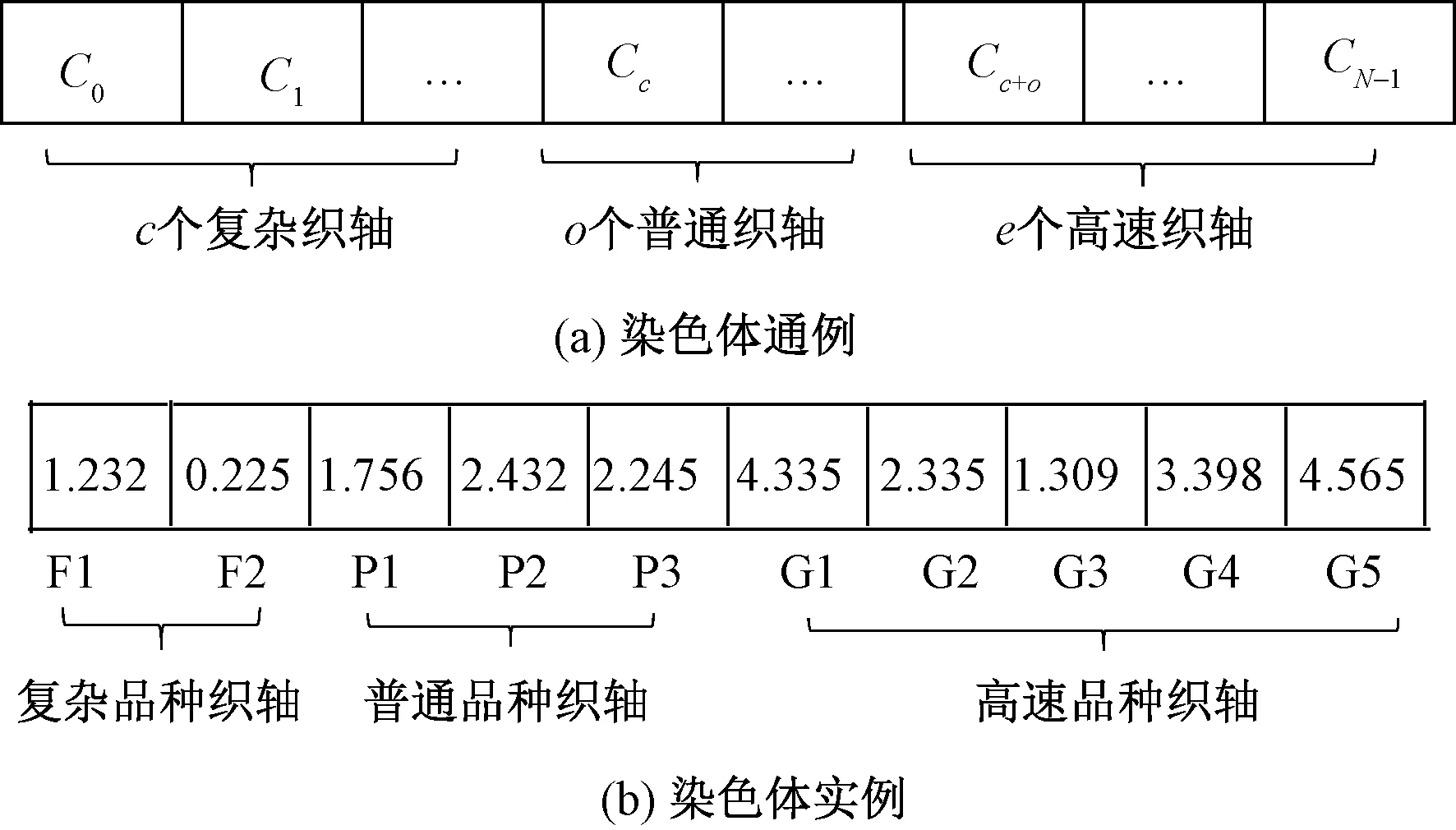
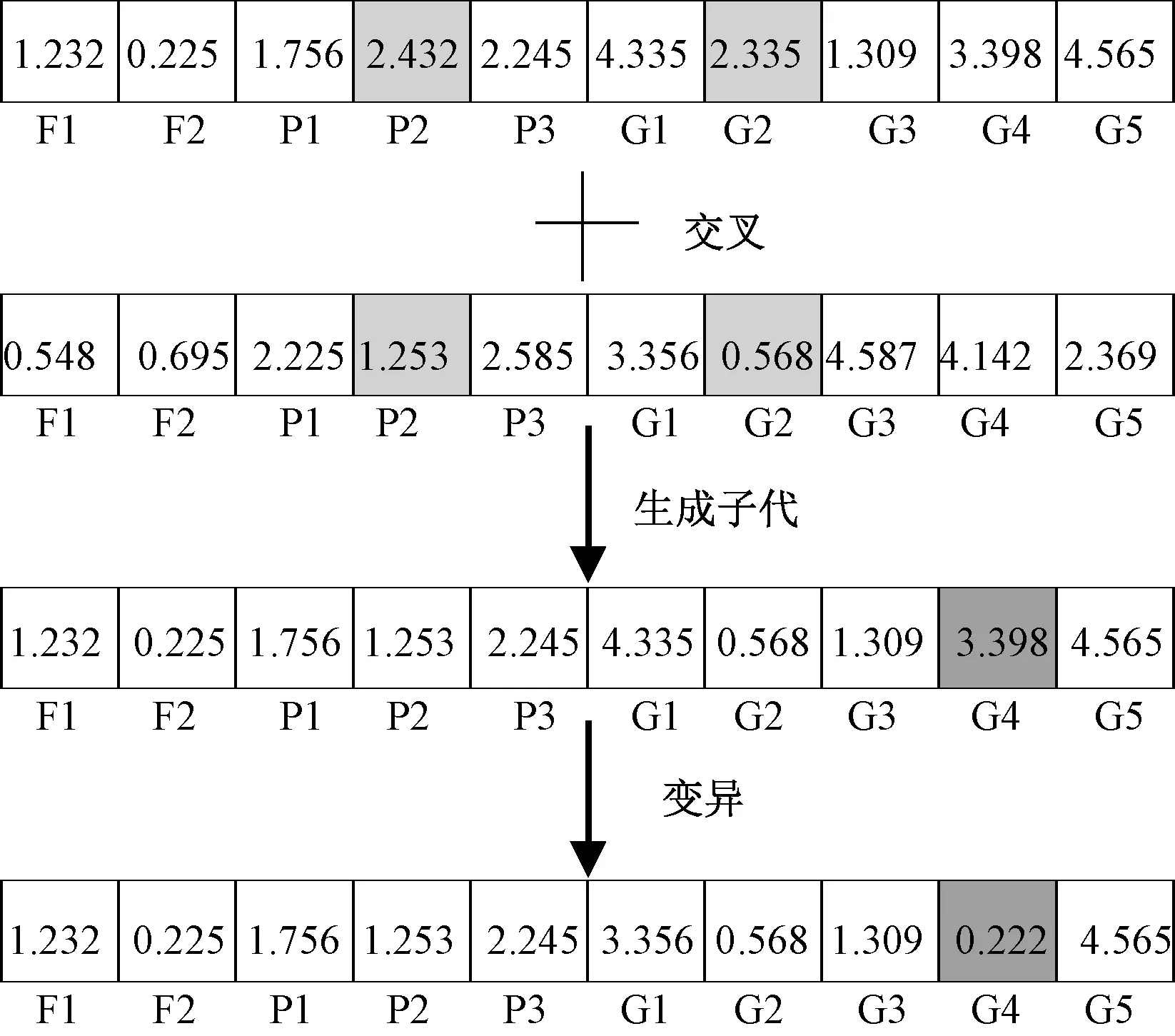
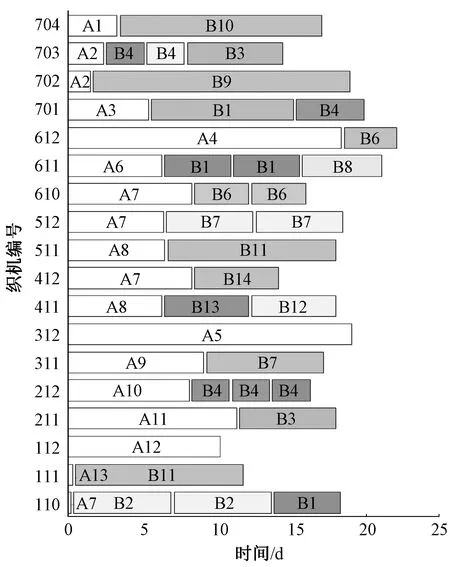
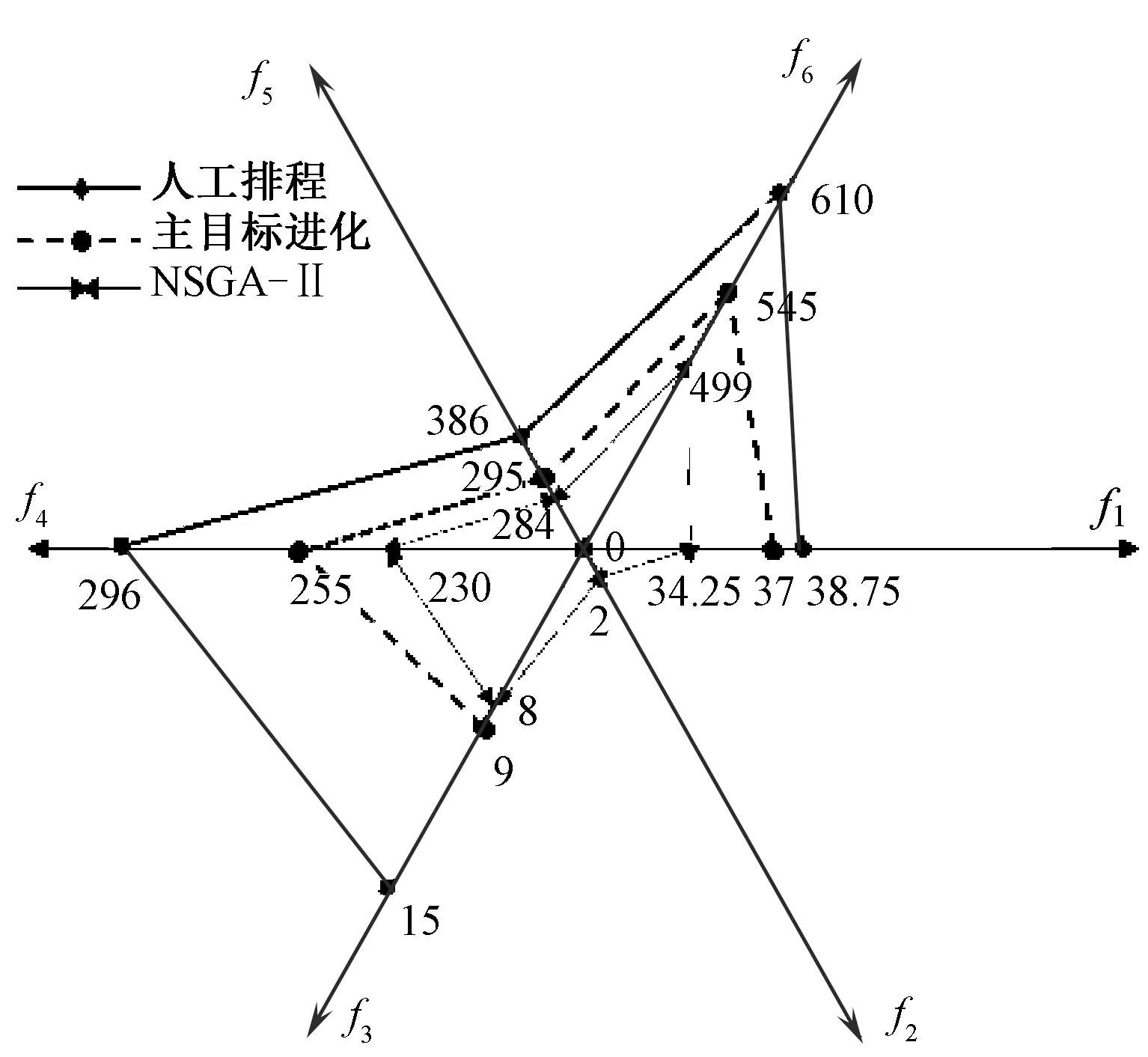
f2=sum(Dt

f3=sum(M0)

目前，人力资源管理信息化软件产品的规则与质量，在社会市场上的标准还不统一，产品还不规范，销售厂商较为混杂，这些问题都在一定程度上制约着人力资源管理的信息化发展。

f4=sum(Pk≠Pk+1)

f5=3n-(3sum(S3)+2sum(S2)+sum(S1))

f6=Q1+Q2+···+Qr

式中：f1为最大完工时间，其取值范围为[Tc,T1+T2+ …+Tm]，Tc为当前时间；max表示取最大值；Ti为第i台织机的完工时间(i=1,2,3,...,m，其中m为织机总数)，完工时间包含织机在织织轴的剩余时间及待安排织轴织造的总时间；f2为订单超期总数,其取值范围为[0,r]；sum表示求总数；Dt为第t个订单截至日期；Ot为第t个订单完成时间(t=1,2,3，...，r，其中r为订单数量)；f3为空车总数，取值范围为[0,m]；M0为机台空车数；f4为品种翻改总数，取值范围为[0,n]，n为织轴总数；Pk表示当前织机第k个织轴的织造品种；f5为机型不合适度，其取值范围为[0,3n]；S3表示合适度系数为3的当前织机织造最合适品种；S2表示合适度系数为2的当前织机织造较合适品种；S1表示合适度系数为1的当前织机可织造品种；若不可以使用当前织机织造此品种，则合适度系数为0；f6为订单占用织机总次数，取值范围为[0,mr]；Qr为第r个订单使用的织机次数(j=1,2,3,…，r，)。

订单占用较少的织机数可减少品种翻改，符合企业的实际生产需要，但会导致完工时间的增加，各目标之间具有一定的矛盾关系，故此问题属于多目标优化问题。而实际的织造排程是以满足订单交期为首要条件，来尽量优化其他目标。

1.3 约束条件

1.3.1 机型约束

织造企业中不同类型的织机适用于不同的品种，并具有一定的交叉性。表1示出某织造企业不同类型织机的品种适应情况。

表1 不同织机的品种适应情况Tab.1 Suitable varieties for different machines

1.3.2 织轴长度约束

织造排程的基本依据是织造时间，织轴的织造时间计算公式如下式所示。本文按照实际工艺计算织轴长度，同时决策者可修改织轴的数量及长度。

式中：Tr为预计织造时间，h；Pw为品种纬密，根/(10 cm)；Lo为织轴上经纱长度，m；j为经纱织缩率；L为织轴回丝长度,m；Ms为织机车速，r/min；η为织造效率，%。

2 主目标进化遗传算法

带精英选择策略的快速非支配遗传算法(NSGA-II)是目前常用的多目标优化算法之一，具有较好的鲁棒性，常用来解决多目标条件下的优选问题[6]。传统的NSGA-II对多个目标同时优化，无主次之分[7-8]，本文对此算法加以改进，设计了 1种主目标进化的遗传算法。

2.1 编码

染色体通例如图 1(a)所示。染色体的总长为织轴总数N，每个基因C的位置对应一个织轴，按照织轴的品种依次表示复杂品种、普通品种、高速品种的织轴。基因C取值都是一个大于等于0的实数(小数位不做限制，图中只是为显示需要)，C的整数部分表示的是对应织轴的待上机编号。织机编号n为从0开始递增的整数，n∈[0,Md)代表多臂织机(Md为多臂织机数)，n∈[Md,Md+Mt)代表踏盘织机(Mt为踏盘织机数)，n∈[Md+Mt,Md+Mt+Me)代表电子织机(Me为电子织机数)。当若干基因的整数部分相同时，对应织轴均使用同一台织机织造，小数部分决定其上机次序，小数部分小的先上机织造。基因C的取值范围由该织轴的适应机型来确定，如复杂品种织轴只可用多臂织机织造，其基因C取值范围即为[0,Md)；普通品种织轴，既可用踏盘织机织造，也可用多臂织机织造，其取值范围即为[0,Md+Mt)；高速品种织轴，可使用所有机型织造，故其取值范围为[0,Md+Mt+Me)。

图1 染色体编码通例与实例Fig.1 General chromosome encoding case(a) and example(b)

本文模型对于织机和织轴的数目没有限制：当织机数变化时，算法可自动根据数据库织机信息，调整相应基因的取值范围；当织轴数变化时，算法可自动根据数据库织轴信息，在染色体对应位置上插入或删除相应织轴，改变染色体的长度，因此，此染色体编码模型具有较强的适应性，满足了品种与织机类型匹配的约束，并可表示织轴的所上织机及上机次序。

本文以一个有5台织机的车间、10个待上机织轴的排程问题为例，介绍编码规则。上述10个织轴包含2个复杂品种织轴，3个普通品种织轴，5个高速品种织轴。上述5台织机均参与织造过程，其中包含1台电子织机，2台多臂织机，2台踏盘织机。此问题对应的一条染色体示例如图1(b)所示。此染色体表示的含义即为：0号多臂织机织造F2号织轴；1号多臂织机依次织造F1、G3、P1号织轴；2号踏盘织机依次织造P3、G2、P2号织轴；3号踏盘织机织造G4号织轴；4号电子织机依次织造G1、G5号织轴。

2.2 种群适应度评价

使用传统NSGA-Ⅱ方法中的快速非支配算法与拥挤度算法来比较不同个体的Pareto支配关系与个体拥挤度，实现对种群进行适应度排序[7]。针对此问题，对于任意的个体解i，其目标函数值分别为f1(i)，f2(i)，…，f6(i)。若对于任意p∈(1,2,3,4,5,6)均有fp(i)≤fp(j)，且存在fp(i)

2.3 选择交叉变异

由于个体之间的适应度值并不是线性关系，因此，采用一种常用的二元锦标赛选择算法。其主要步骤即随机从种群中选择2个个体进入锦标赛，然后按照非支配关系选择适应度最高的个体。

考虑到织轴的安排具有离散性，不受染色体中基因片段位置的影响，对染色体基因顺序要求不高，故分别选择随机个数和位置进行交叉与变异操作，其过程示例如图 2所示。主要步骤即在染色体长度范围内生成随机个数的交叉变异位置，每个交叉变异位置也随机选定，以Pc的交叉率和Pm的变异率分别进行交叉和变异。

图2 交叉变异示意图Fig.2 Crossover and mutation operations

2.4 主目标进化

当应用传统的NSGA-Ⅱ算法时，会对所有的目标同时进行优化，往往会产生订单超期的方案，对于实际织造生产而言，所有的其他目标都是建立在满足交期f2=0的基础上的，一旦存在订单超期，该排程方案即不理想。

基于此，本文将传统的NSGA-Ⅱ算法加以改进，以最小化订单超期数为主目标进行单目标遗传算法进化，当无订单超期后，变为以最小化品种翻改数、空车数、完工时间、订单占用织机次数、机型不匹配度的多目标优化问题。若进化到达设定迭代次数始终存在订单超期时，反馈决策者修改织轴长度或由算法增加织轴数来继续排程。若再次迭代到最终设定次数仍出现订单超期时，说明该订单无法按时交期，算法会直接进行多目标优化，生成最终方案。整个算法的流程如图 3所示。

图3 主目标进化算法(改进NSGA-II)Fig.3 Main objective evolution (improved NSGA-II)

3 实验与讨论

3.1 应用实例

本文以某车间的实际生产情况为例，取工厂的实际订单数据以及织造生产信息，在某一时刻下共拥有60个订单，316个织轴。

本算法使用Java语言编程，并在频率为3.6 Hz的AMD R5-1600X处理器的计算机上运行，对最后排程方案的染色体进行解码，其部分排程甘特图如图4所示。

图4 部分排程甘特图Fig.4 Part of Gantt chart

当应用本文设立的目标函数，各遗传参数取值分别为：交叉率Pc=0.8，变异率Pm=0.01，种群规模N=100，进化代数G=1 000时，采用本文提出的主目标进化遗传算法与普通NSGA-II算法，同时使用工厂的实际排程数据，3种方法目标函数值结果对比如图 5所示。

图5 不同方法的排程效果对比Fig.5 Comparison of different algorithm scheduling of manual scheduling

由图5结果显示，本文算法相较于人工排程，完工时间缩短4.51%，品种翻改减少13.17%，订单占用织机数减少10.65%，空车数减少40%，机型合适度得分提高23.57%，各目标函数评价效果平均提升了15.32%。而普通NSGA-II算法也能取得较好的效果，但由于其各目标权重是相同的，会出现订单超期现象，鲁棒性较低。

应用此主目标进化遗传算法：当处理316个织轴，209台织机，经过一次算法，计算时间用时仅为212 s；而当处理403个织轴时用时为323 s。可以看出，本文采用简化模型，寻求相对最优解，具有较高的运算效率。

3.2 参数讨论

遗传算子参数的选择会影响算法的运行效率，此算法的控制参数主要有交叉率Pc，变异率Pm，若选择固定的Pc、Pm，易使算法陷入局部最优或者出现早熟现象，因此，常采用自适应方法来提高算法的局部和全局寻优能力[9]，而传统的自适应策略依赖于种群的适应度值，对于多目标而言，其适应度值是根据非支配排序得出的，不同代种群适应度值之间不具有可比性，故本文采用了一种动态调整Pc、Pm的方法，自适应Pc、Pm的计算公式如下：

式中：Pm(g)与Pc(g)分别为第g代变异概率和交叉概率；Pcmin与Pcmax分别为最小和最大交叉概率；Pmmin与Pmmax分别为最小和最大变异概率； G为最大进化代数。

应用此公式后使得算法在初期拥有较大的Pc、Pm，随着进化代数的增加，Pc、Pm逐渐减小，从而使得算法可在运行初期拥有较高的种群多样性，在后期利于保留最佳个体而进行细致搜索。当使用Pc=0.8、Pm=0.01时，算法各目标函数值经归一化，并映射到0～100范围内的函数值随进化代数的收敛曲线如图6 (a)所示，图中所示数值为最终代数的适应度函数值。而使用自适应Pc、Pm后，对于Pc、Pm最大、最小值在一般推荐范围中取值[10]，Pcmin=0.4，Pcmax=0.99，Pmmin=0.001，Pmmax=0.1，优化后目标函数的收敛曲线如图6 (b)所示。

图6 主目标进化遗传算法与采用自适应后的收敛曲线对比Fig.6 Comparision of convergence curves of main objective evolutionary genetic algorithm (a) and using adaptive methodhm (b)

对比图6(a)、(b)可知，优化前后算法均在前期朝着订单超期数为0的方向快速收敛。优化前算法在70代左右订单超期数即可变为0，但随着种群的不断进化，其他目标函数值的进化却较为缓慢，而且算法会出现订单超期数大于0而无法收敛的现象，原因是由于算法早熟，使种群多样性降低，进化能力丧失。当使用自适应方法进行优化后，算法在80代左右开始收敛，并且在进化后期存在着多次进一步寻优的过程：表明了使用自适应方法后算法可提高全局搜索能力，在一定程度上避免早熟现象；另一方面，应用此自适应的多目标优化方法避免了由于遗传参数的选择对算法效果的影响，且对算法运行效率并无较大影响。

应用自适应遗传参数，对算法进一步优化后，按照支配关系取最优个体，其各目标的函数值为：[36.34, 0, 276, 5, 269, 567]。相较于使用固定的Pc、Pm，完工时间缩短0.06%，品种翻改减少1.51%，订单占用织机数减少1.43%，空车数减少50%，但机型合适度得分降低了1.42%。总体而言应用自适应遗传参数后算法的鲁棒性进一步提高，并可应用于实际排程计划中。