基于知识欧姆定律的产品开发耦合活动重叠时间研究

田启华 刘泽龙 杜义贤 周祥曼

(三峡大学 机械与动力学院，湖北 宜昌 443002)

传统的串行执行模式己经不能满足新产品快速、及时的上市，但是完全并行的执行模式又会带来额外的成本损失，使得产品的总体收益达不到预期效果.因此，两者之间的重叠执行模式就变成当今企业和学者们的研究重点[1].作为产品开发的一个重要迭代模型，活动间的重叠执行模式可以有效缩短产品开发周期，但也会带来额外成本的增加[2]，所以需对其合理有效的规划.

对于产品开发重叠执行模式的研究，国内外学者获得了一些可喜的成果.例如：Reza Dehghan等[3]描述了设计活动间重叠执行特点，分析了活动重叠成本和时间权衡问题，提出了等效返工时间的概念，给出多个活动重叠的情况下时间和成本权衡问题的计算模型.Lim Tae-Kyung等[4]对活动重叠属性进行了简单的描述，对时间成本权衡问题进行了分析，给出了返工时间和工期的数学表达式，在不分配额外资源的情况下确定了活动的最佳重叠度，达到减少时间和成本的目的.武照云等[5]描述了上游活动的信息进展特性，对考虑综合信息影响量的信息交流策略进行了分析，针对两种不同的重叠模式建立了统一的重叠规划时间模型.

活动间信息的交流可以看作是知识在活动间的转移，不少学者从知识的角度结合欧姆定律定性地描述了知识压、知识流、知识阻等概念[6].柳飞红等[7]对隐性知识的特征进行了描述，从欧姆定律的角度结合隐性知识的特点提出了隐性知识分享模型，研究了隐性知识分享过程中各种障碍因素并给出了相应的对策；Denise

Cumberland等[8]分析了隐性知识转移的5个障碍—信任、成熟、沟通、竞争和文化，提供了促进知识转移的方法；但上述研究只是对知识转移过程进行了定性分析，未能对其定量分析与研究.陈友玲等[9]结合知识欧姆定律的概念，运用函数描述活动间知识转移过程中存在的知识势和知识阻的变化，建立了活动重叠执行的时间模型.但该研究只考虑了信息流的单向传递，未考虑活动间可能存在的耦合问题.

本文针对以上研究的不足，从知识的角度结合欧姆定律分析耦合活动重叠执行特性并建立时间模型；研究下游活动的介入时间和知识转移次数对全局收益的影响，根据全局收益最大化原则，利用优化仿真方法求解出下游活动最佳介入时间和最佳知识转移次数，从而为产品开发过程的合理规划提供决策参考.

1 基于知识欧姆定律的耦合活动重叠特性分析

类似于欧姆定律中电压、电流以及电阻的定义.①知识压：上、下游活动之间信息交流在知识存量上存在的不同，形成的知识势差；②知识流强度：在知识转移过程中，上、下游活动可以看作闭合电路中电源的正负极，知识转移的效果看作电路中流动的电流；③知识阻：知识转移过程中阻碍知识流动的因素.下面将基于知识欧姆定律的原理对耦合活动重叠执行、知识转移过程等进行分析.

1.1 耦合活动重叠执行描述

为了缩短产品开发周期，在上游活动还未结束时下游活动开始介入，此时上、下游活动在时间轴上就会形成重叠.在重叠执行过程中，设计活动间会进行多次信息交流以传递产品开发相关知识，因此，可以将每次信息交流看成设计活动间知识的转移.在知识转移过程中，将单位时间内的知识转移量称之为知识流强度.显然，知识流强度的大小反应了知识转移的速度，知识流强度越大，知识转移的速度就越快，反之，知识转移的速度就越慢.从宏观上看，知识流的方向是由知识存量较高的上游活动流向知识存量较低的下游活动，但事实上，知识流的方向是双向的，下游活动由于上游活动传递的不完善知识会向上游活动发送反馈知识，但相比上游转移到下游的知识含量要小得多.这种现象类似于物理学中的电流，在外电路中，电流的流向是由电势较高的正极流向电势较低的负极.事实上，电流的方向只是正电荷定向流动的方向，而回路中电荷的载体电子既有从高电势点流向低电势点，也有从低电势点流向高电势点.

1.2 知识转移过程描述

由于两个串行耦合活动是多个串行耦合活动重叠模型的基础，本文将以两个串行耦合活动间的重叠执行为研究对象.在知识转移过程中，耦合活动间在信息交互上存在着相互依赖的关系，上游活动在重叠执行阶段传递给下游活动的不完善或错误知识必然会引起下游活动的迭代返工，即延长了下游活动的迭代执行时间.当上游活动的不完善或错误知识在下游活动进行迭代求解的过程中被发现，并把错误的知识反向传递给上游活动时，上游活动就需要对之前产生的错误知识进行修改返工，即延长上游活动的设计时间.

在对知识转移过程描述时需做出如下假设：①假设上、下游知识转移时间为零；②假设在重叠执行期间内，上游活动与下游活动进行了n次知识转移，每两次知识转移时间间隔相等；③假设下游活动在迭代执行过程中发现了错误的知识，但不立马将错误知识反馈给上游活动，而是在下一次知识转移时再反馈给上游活动.

上、下游活动知识转移过程如图1所示，上游活动A开始设计一段时间后下游活动B开始执行，假设上游活动在tAS=0时刻开始执行，预计完工时间为TA，下游活动在tBS=t1(t1为第1次知识转移时间，tAS≤t1≤TA)时刻开始执行，预计完工时间为TB，在重叠期间t1到TA时间段内进行了n次知识转移，则两次知识转移之间的时间间隔为t=ti+1-ti=(TA-t1)/(n-1)(ti、ti+1分别为第i次、第i+1次知识转移时间，i=1，2，…，n-1).

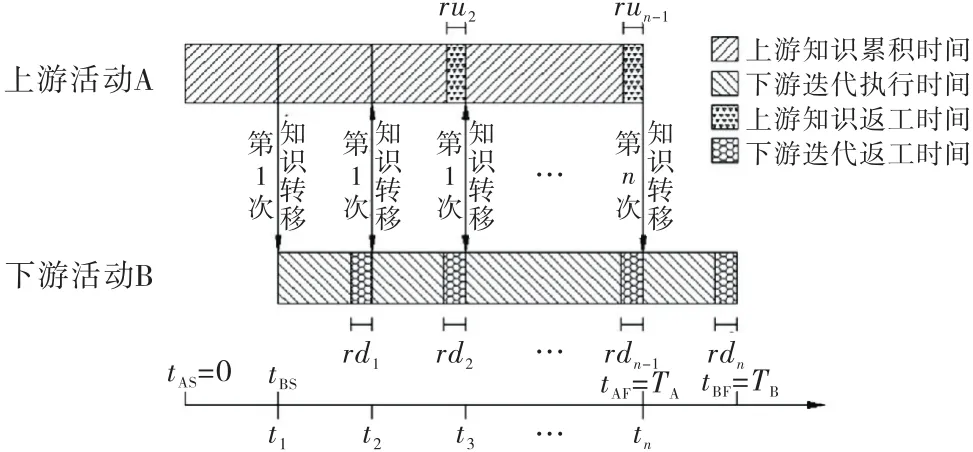
图1 知识转移过程示意图

2 耦合活动重叠执行时间模型的构建

2.1 知识存量函数与知识阻函数的构建

上游活动在开始设计工作后，随着时间的推移会不断地产生和累积产品开发方面的知识，从而形成上游活动的知识存量，参考文献[10] 提出的知识累积率函数，定义上游活动的知识存量函数如下：

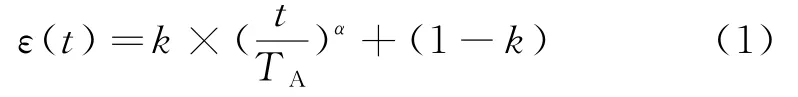
式中，ε(t)表示上游活动的知识存量，t表示为上游活动的执行时间，0≤t≤TA，TA为上游活动的预计完成时间，k为上游活动知识创新度指数，α为上游活动的知识累积演化路径指数，由具体活动特性所决定，为简化模型本文取α=1.

根据对设计活动的影响作用可以将知识阻分为知识内阻和知识外阻[7]，但本研究将上、下游活动在知识转移过程中所涉及的知识阻统一用R表示.随着知识转移次数逐渐增加，上、下游活动双方对产品开发任务越来越熟悉，知识阻R会随着知识转移次数的增加逐渐减小.为了简化模型借助学习曲线理论[11]来描述知识阻的减少量，则知识阻函数可表示为：

式中，i为知识转移次数；Ri为第i次知识转移时的知识阻；γ为迭代因子；知识转移方和接收方在第1次知识转移时与二者之间知识势差存在一定关系，参考文献[6] 中界面知识阻与知识位势差的函数关系，设第1次知识转移时的知识阻R1=ε(t1)/t1.

2.2 知识返工时间函数的构建

在知识转移过程中，知识的难易度会一定程度地影响下游活动的知识返工量.因为上游活动累积的产品相关知识越难，当传递给下游的知识存量越低时，下游的设计工作越难进行，导致下游活动迭代返工量随着增大.当上游活动的知识累积量越多，转移给下游活动的知识也就越多，意味着下游活动需要做出的估计假设越少，从而知识返工量也越少.参考文献[12] 中返工率函数的构建，定义下游活动知识返工率函数如下：

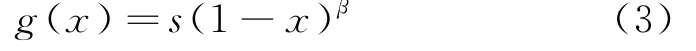
式中，s为上游活动的知识难易度系数，0≤s≤1；x为上游活动知识存量，0≤x≤1；β为下游活动设计人员的技术能力指数，β≥0.

将式(1)代入式(3)可得下游活动的知识返工率函数g(t)为：

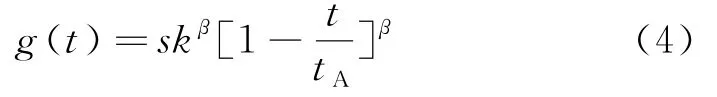
下游活动的知识返工时间可以用其知识返工率函数的积分形式表示，则下游知识返工时间rdi为：

如果将下游活动发现不完善知识或错误知识视为概率事件，那么可以将下游活动发现知识错误的过程假设成一个强度为μ(t)的非稳态泊松过程.参考文献[13] 建立关于该随机过程的数学模型：

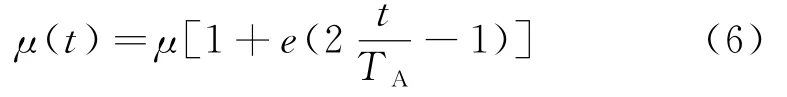
式中，TA为上游活动预计完成时间，0≤t≤TA；e是反应上游活动进展速率的参数，-1≤e≤1.μ为平均泊松强度，一般由经验值获得.

上游活动的返工时间一方面取决于上游活动对下游活动反馈的错误知识的可变程度，可变程度高意味着上游活动会根据下游活动反馈的错误知识做出较多的错误修改，从而上游活动返工量越多，反之则越少；另一方面下游活动累积的知识越多，能反馈给上游活动真实有用的知识就越多，上游活动的返工量就越小，因此返工率函数应该是一个非递增函数，参考文献[13] 运用线性函数构建上游活动返工率函数：

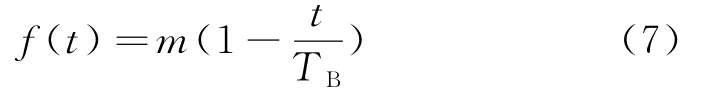
式中，m为上游活动的可变度，0≤m≤1；t为下游活动的进展度，0≤t≤TB.

根据以上对上游活动返工时间的分析，第i次迭代后上游知识返工量应由下游活动发现错误知识的概率与上游活动的返工率共同决定，定义上游活动知识返工时间rui为：

将式(6)和式(7)代入上式，可得上游活动知识返工时间rui为：

2.3 基于欧姆定律的目标决策模型的构建

在知识转移过程中，类似物理学中的欧姆定律，定义知识流强度为知识压UAB(t)与知识阻R的比值，由此知识流强度I(t)可表示为：

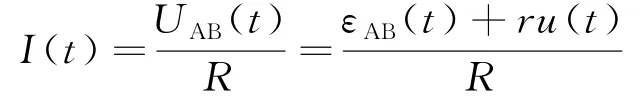
将式(1)、式(2)和式(8)代入上式，可得第i次知识转移中知识流强度I(ti)为：

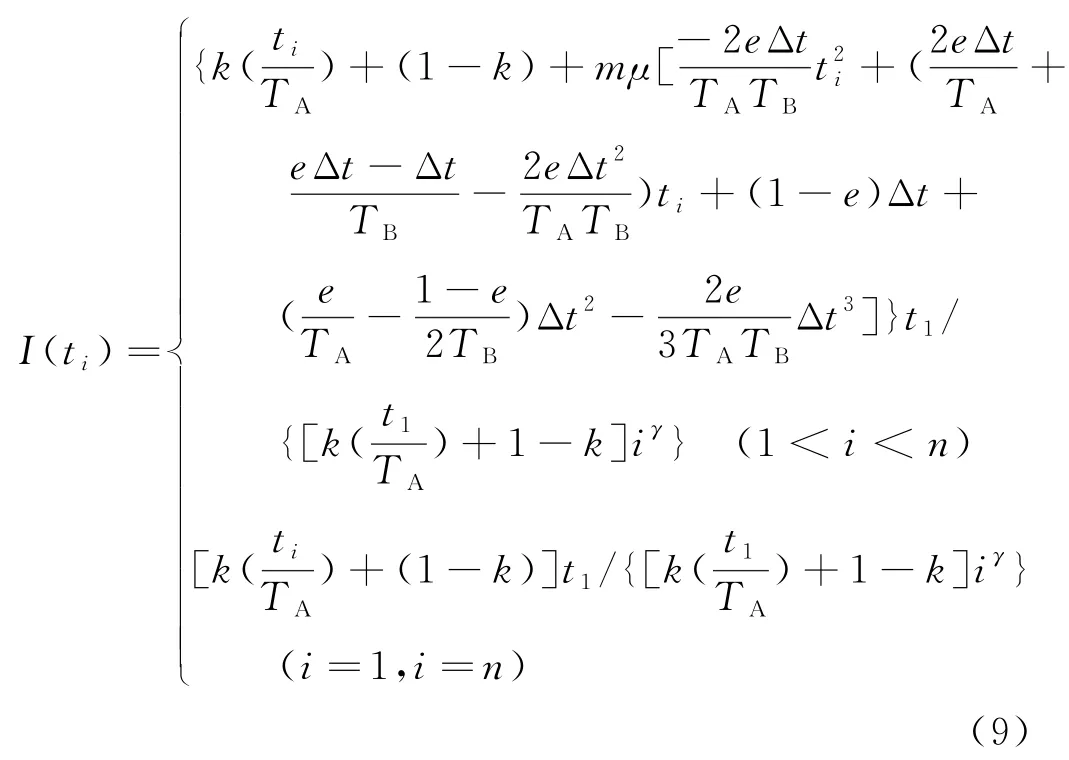
类似物理学中电量的计算公式，知识转移过程中知识转移量的大小用知识流强度与知识转移时间Δt的乘积来表示，所以在第i次知识转移过程中有效知识转移量Qe(ti)为：

第i次知识转移过程中无效知识转移量Qr(ti)用知识流强度与下游活动知识返工时间的乘积来表示，即

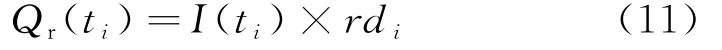
假设将总的有效知识转移量作为下游活动提前介入所得的总收益，总的无效知识转移量作为付出的总成本，则下游活动提前介入的收益Qi为：

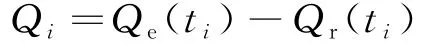
将式(9)～式(11)代入上式，可得第i次知识转移过程中的收益Qi为：

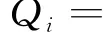
由上式可得，上、下游活动在重叠期间内的全局收益为：

由此将上述问题转化为如下优化模型：

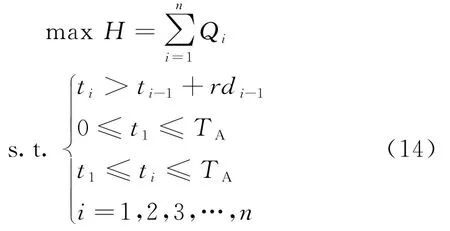
3 基于Matlab仿真优化求解

运用数学解析法对耦合活动重叠执行模型进行求解时，计算过程不但复杂，且表述也不够直观，而仿真优化方法能简化数学计算，并能有效描述模型中的动态变量以及对动态变量进行仿真模拟.因此，本文采用Matlab仿真求解方法对耦合活动重叠执行的时间模型进行求解.根据下游活动不同的介入时间分别计算出不同初始状态下的参数，然后运用Matlab对使全局收益最大化的下游活动介入时间和知识转移次数进行优化.具体仿真优化步骤如下：

步骤1：设定知识转移总次数n的取值范围集合A={n1，n2，n3，…，nn}，令其初始值n=n1.

步骤2：初始化变量，全局收益H=0，下游活动开始时间t1=0，时间步长step=1，知识转移次数i=1.

步骤3：计算每次知识转移后的获得的收益Qi，更新全局收益H=H+Qi.

步骤4：启动仿真进程，i=i+1.若满足条件i≤n，直接转步骤3，否则转步骤5.

步骤5：计算全局收益H的值，并将其值存入结果矩阵R中，令t1=t1+1.

步骤6：判断重叠执行循环部分是否结束，若满足条件t1≤TA，则直接转步骤4，否则，令n=n+1，转步骤7.

步骤7：判断是否满足仿真结束条件，若满足条件n∈A，则直接转步骤6，否则转步骤8.

步骤8：仿真过程完成，输出结果矩阵R.

如图2所示，将上述步骤转换成如下的仿真过程流程图.

图2 仿真过程流程图

4 实例分析

以某摩托车发动机的开发过程为例进行应用分析.该企业的柴油发动机开发主要由产品设计部(上游活动A)和制造部(下游活动B)参与，设计部负责设计产品的结构、功能等，上游活动的设计人员工作一段时间后将累计的知识传递给下游活动，下游活动的设计人员得到上游活动提供的生产相关知识后开始进行制造生产.在该摩托车发动机的开发过程中设计人员会与制造人员进行多次信息交流，设计人员会根据制造人员反馈的知识不断进行设计更改，并将更改后的知识再次传递给制造人员，如此反复直到整个产品开发过程完成.

在产品开发的设计方案通过审批后，通过对产品设计部和制造部的人员进行问卷调查，结合专家以往类似设计经验对模型涉及的参数值进行评估.相关参数的取值见表1.

表1 相关参数取值

研究中，下游活动的介入时间和知识转移次数是影响全局收益的两个原因.为了寻找最佳的下游活动的介入时间和知识转移次数n，应尽可能多地计算出不同参数组合对应的全局收益，但为了仿真结果图表达更加简洁明了，本文取10≤n≤20.在仿真过程中本文只考虑重叠执行情况，即t1的取值范围为1≤t1≤29，以上述案例为基础在Matlab进行仿真计算的结果如图3所示.

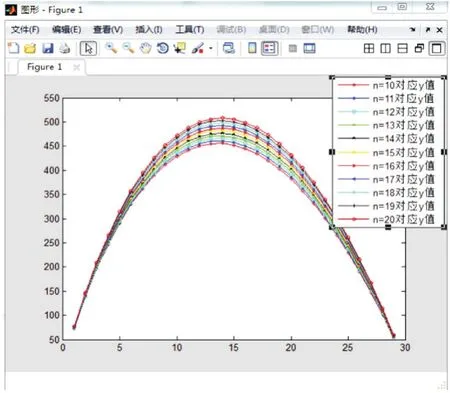
图3 仿真结果图

由图3可知，随着知识转移次数n的取值不断增大，上、下游活动交流次数增多，每次知识转移过程中下游活动从上游活动获得的不完善知识或错误知识相对减少，从而使下游活动迭代返工时间逐渐减小，而全局收益逐渐增大，从该模型中可以看出n的取值越大越好，但是实际情况中考虑信息交流成本及工作协调等因素的影响.为了更准确地分析下游活动介入时间对全局收益的影响，从仿真结果中提取n=15对应的下游活动介入时间t1与全局收益H的数据，见表2.

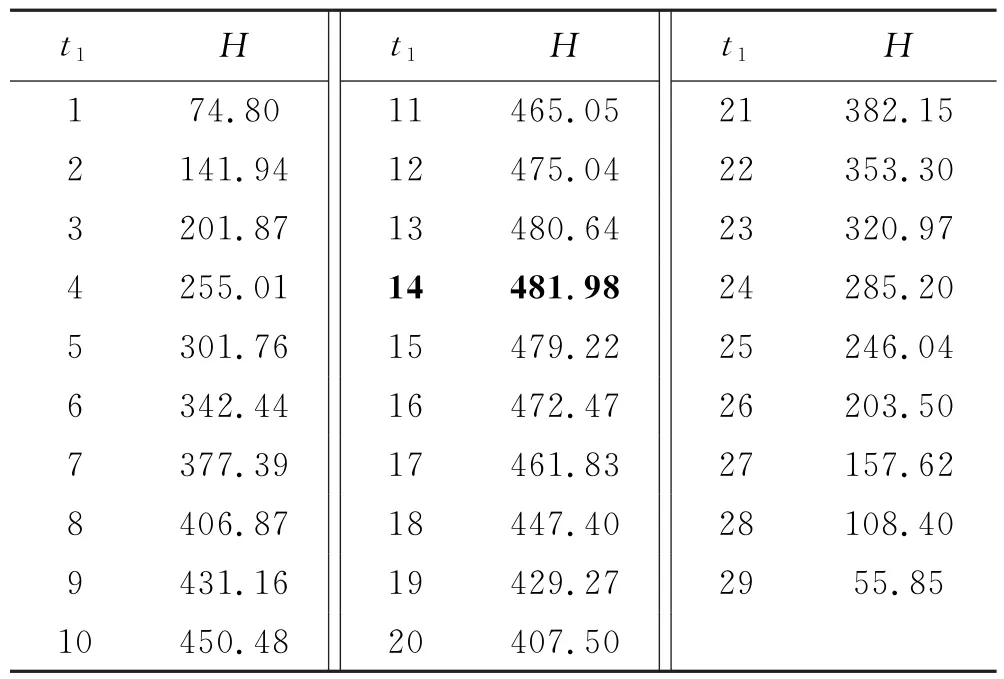
表2 n=15对应的仿真数据

由表2可知，当下游活动介入时间不断增大时，全局收益先增大后减小，当下游活动介入时间t1=14 d时，全局收益H=481.98达到最大.因此，对于该模型最佳的解决方案是当上游设计部门进行14 d后，下游制造部门开始介入，并和上游设计部门一起作业.

5 结 语

本文基于知识欧姆定律的概念对产品开发中两个串行耦合活动的重叠执行特性进行了分析.建立了上游活动知识存量函数和知识转移过程中知识阻函数及知识流强度函数.分别构建了上游活动和下游活动的知识返工率函数，并以此计算出上、下游活动的知识返工时间.在此基础上，构造了基于全局收益最大化的耦合活动重叠时间模型，运用Matlab采用仿真方法对该模型进行求解.最后结合实例分析，求出了使全局收益最大化的下游活动最佳介入时间.结果表明，本文提出的方法对产品开发过程中耦合活动重叠执行模式合理规划和科学指导有一定的参考作用，验证了该方法的有效性和可行性.