沙土固化场地板式地锚的抗拔特性研究

2019-08-28朱晓虎肖俊俊

三峡大学学报(自然科学版) 2019年4期

朱晓虎殷敏肖俊俊杜伟

(1.国网安徽省电力公司电力经济技术研究院，合肥 230071；2.安徽华电工程咨询设计有限公司，合肥230022)

在我国“西电东输”工程中，存在着大量输电线路需要穿越沙漠地区，沙土的性状较为松散，作为输电线路杆塔基础的地基土体在外荷载的作用下易发生变形，而输电线路杆塔在外荷载作用下的抗变形措施可采用锚板斜拉[1]，明确锚板在上拔过程中土体的变形破坏形态是合理确定锚板极限承载力的重要前提.一般情况下，在对沙漠地区杆塔基础进行施工时，需先对场地地基一定范围内的沙土进行加固，以提高地基的承载力，目前常采用水泥对沙土地基进行加固[2-3].此外，国内外对承受水平和竖直荷载的锚板进行了大量研究，提出了不同的地基土破坏模式和锚板承载力的计算方法.例如Murray和Geddes[4]基于试验研究了不同形状锚板、不同埋深等因素对承载力的影响；丁佩民等[1]开展了砂土中的模型锚板上拔试验，研究了砂土密实度、锚板埋深、锚板几何形状、上拔的倾斜角度对锚板承载力的影响.胡宏[5]通过室内模型试验分析了上拔过程中水平条形锚板的承载力、锚板周围砂土的件模拟了试验过程，进一步讨论了锚板承载力特性的演化过程.张昕[6]等采用数字图像关联技术对不同密实度砂土中锚板在上拔过程中周围土体的变形场进行了研究，并建立了锚板承载力力学模型.

上述研究主要集中在水平和竖直荷载作用下锚板的应力变形情况.实际工程应用中，根据使用类型和荷载方向，经常需要倾斜埋设锚板，并且对于承受倾斜上拔的锚板研究，也有学者开展了相关研究.例如，Merifield等[7]应用极限分析和位移有限元分析方法，对不排水粘土中倾斜锚板的稳定性进行了评价.刘君等[8]通过三维弹塑性有限元方法研究了均质饱和黏土中圆形锚板的承载力，探讨了埋深和上拔倾角对锚板承载力的影响并给出了承载力的简单计算公式.但是目前在这方面的研究还不够深入，在工程设计过程中，确定地锚承载力时通常假定锚板周边土体沿直线破裂面发生破坏[9].事实上，研究表明抗拔锚板的极限承载力与破裂面的形状密切相关，破裂面的形状并不能简单的假定为直线或曲线形[10].

本文结合输电线路施工中常采用的板式拉线地锚，通过室内三轴压缩试验，测得水泥加固后风积沙试样的物理力学参数；在此基础上，开展数值模拟研究，分析该类地锚极限承载力和锚板周边土体的破坏形态，对于认识沙漠地区加固风积沙场地倾斜锚板在外荷载作用下的变形破坏机理及量化分析其极限承载力具有重要的理论意义.

1 室内三轴试验

1.1 试样制备

参考文献[2-3] 的关于沙漠地区水泥固化风积沙物理力学性质研究的相关成果，采用水泥对新疆地区风积沙(密度1.55 g/m3、含水率1.7%、孔隙比0.98，其级配曲线如图1所示)进行加固，加固试样的具体制备过程如下：

1)取风积沙1 000 g备用.

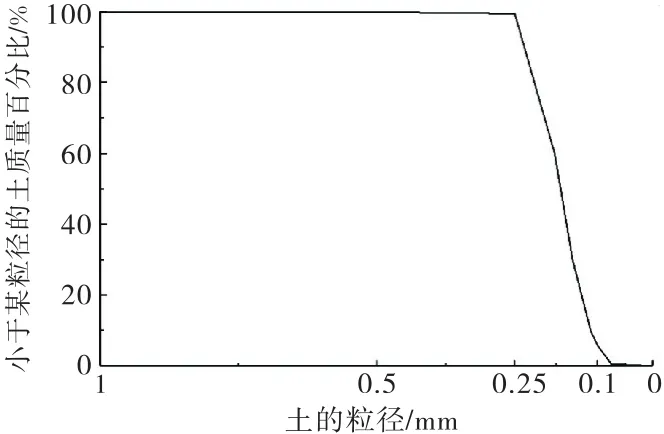
图1 天然风积沙级配曲线

2)取准备好的水泥、纯净水、风积沙，将30 g水泥与风积沙进行混合并搅拌均匀，再加入40 g纯净水，混合搅拌，制成水泥与风积沙的混合散粒料，并置于塑料桶中用保鲜膜封存1 d.

3)将水泥与风积沙的混合散粒料取出，置于内径为3.19 cm的制样器中，按试样高度(8 cm)分3层击实，制成直径为3.19 cm、高为8 cm的圆柱体试样，共16个.

1.2 试验仪器及参数设置

试样的三轴压缩试验在TSZ系列全自动三轴仪上进行.具体加载控制参数为：围压的施加采用荷载控制，以50 k Pa/s的加载速率加载到设定的围压值；此后，轴向加载采用位移控制的方式进行，以0.08 mm/s的加载速率压缩试样至破坏.

1.3 试验结果

三轴测试获得不同围压下沙土固化试样的典型应力-应变曲线(每个围压4个试样，通过取平均的方式获得不同围压下峰值抗压强度)，如图2所示.根据不同围压下试样的峰值抗压强度绘制莫尔应力圆及其公切线，求得测试试样的内摩擦角和凝聚力，风积沙加固试样的物理力学参数见表1.

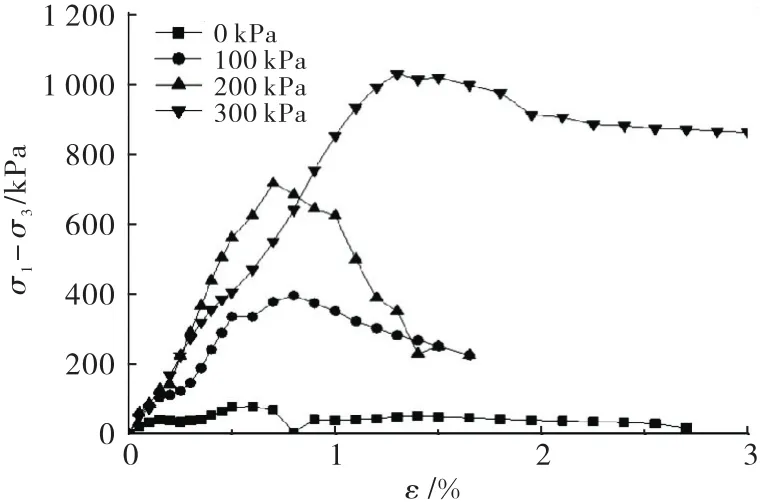
图2 试样在不同围压下的应力-应变曲线

表1 风积沙加固试样的强度与变形参数

从表1可以看出，1 000 g风积沙掺入30 g水泥，与40 g纯净水搅拌后制成的试样可以将风积沙的凝聚力从0 k Pa提升至43 k Pa，说明采用水泥作为胶凝材料对风积沙的加固效果良好.

2 数值模拟分析

2.1 基本理论

在输电线路工程中常采用的地锚形式包括木质地锚、钢板式地锚、重力式地锚和立式桩地锚.其中钢板式地锚为定型加工，施工方便，应用较为广泛，其埋设方法如图3所示.

图3 钢板地锚示意图

以往类似工程的实践经验表明，钢板地锚在斜向上45°荷载作用下的变形破坏主要表现为地锚附近土体在斜向上45°荷载作用过程中出现局部的塑性变形，并逐渐累积而形成贯穿的滑移面，最终导致土体发生整体破坏.本文采用数值模拟方法，主要研究地锚在斜向上45°荷载作用下的承载性能及破坏模式.

在斜向上45°荷载的作用下，地锚结构周围的岩土体首先经历线弹性阶段直至达到屈服阶段，屈服后的岩土体会发生塑性变形，甚至发生破坏，因此，采用弹塑性理论来分析地锚周围岩土体的变形破坏情况.地锚结构则与周边岩土体大不相同，由于地锚结构是采用钢材加工而成，其物理力学性质远大于岩土体，通常情况下，在外荷载的作用下钢材只会发生弹性变形，而不会发生屈服破坏，因此采用弹性理论对地锚结构的变形情况进行分析.地锚结构在外荷载的作用下会产生一定程度的位移，在此过程中，作用于地锚结构上的荷载会通过地锚结构与周边岩土体的接触面将荷载传递给周边土体，并且地锚结构及其周边岩土体主要通过摩擦作用传递荷载，而在接触面上产生的摩擦力与切向变形、法向变形之间呈线弹性关系，所以采用无厚度的接触面力学模型对接触面的应力变形情况进行分析.

2.2 数值模拟

2.2.1 三维数值计算网格模型的建立

三维数值网格模型采用ANSYS建立，随后采用接口程序将模型导入有限元差分软件FLAC3D进行计算.

根据钢板地锚示意图(如图4所示)中地锚结构的尺寸建立地锚数值网格模型，并确定合适的地基范围.模型的总尺寸为长13.6 m，宽12.5 m，高8.7 m；其中回填风积沙的尺寸为长2 m、宽0.8 m、深度3 m(见图5)；回填风积沙四周和下方6m的范围内为加固的风积沙.地锚结构与其周边岩土体的单元采用8节点六面体单元进行划分，地锚结构与地基岩土体之间的接触面采用无厚度的接触面单元进行模拟；根据土体与地锚结构之间的距离，采用从密到疏的方式划分网格，地锚数值网格模型共划分292 619个单元，243 675个节点(如图5所示).

图4 地锚尺寸图

图5 模型尺寸图

2.2.2 计算参数

根据上文室内三轴试验的测试结果，结合相关的工程资料确定原状风积沙及加固后风积沙的物理力学参数(见表2).

表2 加固前后风积沙物理力学参数

采用工程类比的方法，确定地锚钢板的弹性模量E为210 GPa、泊松比μ为0.33，钢丝绳弹性模量E为110 GPa、泊松比μ取0.33；锚板与风积沙及水泥加固后的风积沙接触面的物理力学参数见表3.

表3 接触面物理力学参数

2.2.3 材料本构模型及屈服准则的选取

根据图2可知，水泥加固后的风积沙在加载压缩过程中的应力-应变关系曲线形态表现出明显的峰前强化与峰后软化的特征.随着围压的增大，虽然应力-应变关系曲线峰后下降段逐渐变得不明显，但在整个过程中峰前强化和峰后软化的特征仍然可以体现出来.因此，地锚周边加固风积沙的本构关系选择具有明显峰前强化与峰后软化的应变强化软化弹塑性本构模型.通过FLAC3D软件二次开发，将图2所表达的典型应变强化与软化特征嵌入到软件中，进行上拔过程中锚板的变形破坏分析.具体地，采用FLAC3D中的FISH语言，对加固风积沙的本构模型进行二次开发，基于此计算获得200 kPa围压下加固风积沙试件压缩过程的应力-应变关系(数值试验)，其与室内压缩试验获得的结果对比如图6所示.

图6 二次开发获得的加固沙土应力-应变关系与试验结果对比图(围压200 kPa)

从图6中可以看出，二次开发获得的本构模型能够很好地再现试验获得的加固风积沙应力-应变关系.地锚结构采用钢板材料，在其受斜向上的荷载作用过程中始终处于弹性状态，其本构模型选取弹性本构模型.地锚结构在斜向上45°荷载作用下，其周围地基土体会发生不同程度的塑性变形，在该过程中地基土体可能出现张拉破坏和剪切破坏，本次计算过程中采用的屈服准则应能同时体现出张拉破坏和剪切破坏，因此选择Mohr-Columb屈服准则与张拉破坏相结合的复合准则，作为地基土体的屈服准则.2.2.4 边界条件及加载方式

根据斜向荷载作用下地锚结构受力特征，设置数值网格模型(见图5)的4个侧面及底面均采用法向约束，模型上表面为自由边界.

计算过程中，选取地锚结构中U型环截面上的节点(如图7所示)，通过对节点施加节点力的方式对地锚进行逐级加载直至地锚周边土体发生破坏，荷载的方向与水平方向的夹角为45°(工程中常设置的锚板上拔方向)，每一级荷载的大小为20 k N.

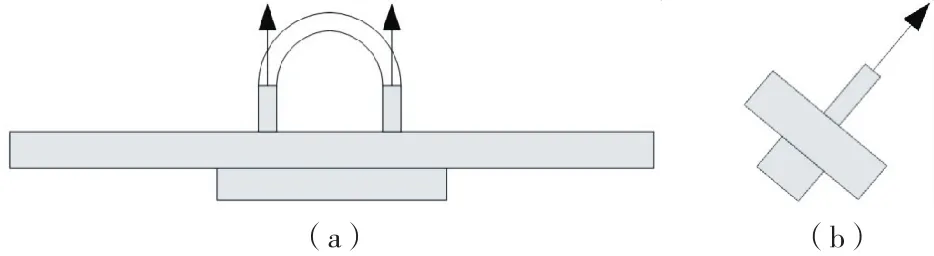
图7 模型荷载施加情况

2.3 荷载作用下地锚承载力及土体变形破坏分析

2.3.1 地锚结构及土体Q-S曲线

荷载位移曲线是描述外荷载作用下基础变形破坏特征最直观的表现方式之一，工程中常把荷载位移曲线获取的基础抗拔承载力作为设计的主要依据.本文通过运用FLAC3D软件对钢板地锚的斜向上拔过程进行数值模拟计算，根据地锚结构以及周围土体监测点(如图8～9所示)的位移监测值，绘制出地锚结构和土体在Z方向的荷载-移曲线(如图10所示).

图8 剖面位置图

图9 监测点位置图

由图10可以看出监测点的荷载位移曲线变化整体表现出“先缓变后陡变”的趋势.当地锚所承受的荷载较小时(小于40 k N时)，土体和地锚二者位移均较小，且随荷载的逐级施加基本呈线性变化，荷载位移曲线近似成直线；随着荷载的继续增加，土体和地锚的荷载位移曲线斜率都逐渐变大，位移的增加幅度均变大.

图10 地锚结构及土体的荷载位移曲线

在整个上拔过程中，由于A点处的土体位于地锚上方，使得土体处于压缩状态，锚板与土体二者同时运动，其荷载位移曲线重合.随着荷载的逐渐增大，B、C点处的土体和地锚位移增长出现差别，土体和地锚之间出现相对位移，当荷载达到比例极限2.0×105N之后，随着荷载的继续增加，地锚的位移量相对于同一点处的土体位移量要显著的多(如图10(b)、(c)所示)，且差距不断增大，这表明地锚与周边的土体脱离，在这些区域的土体已经发生剪切破坏.一些学者通过模型试验对钢板地锚及其周边土体进行研究发现，锚板在上拔过程中板前后侧土体均会发生局部剪切破坏[11].当荷载继续增大，超过2.4×105N时，土体的位移急剧增加，此时监测点A处的土体位移达到7.3 cm，土体逐渐丧失承载能力.

2.3.2 塑性区分析

在数值模拟的过程中采用逐级加载的方式对钢板地锚施加荷载，每级荷载为2×104N，共12级，现取1.2×105N、1.6×105N、2.0×105N和2.4×105N荷载作用下塑性区分布图(如图11所示)进行分析.由图11可知，作用在地锚结构上的荷载较小时，土体中产生塑性区的范围较小，主要集中在地锚结构的下方和左上方(见图11(a)、(b))；随着荷载增加，土体中塑性区的范围逐渐扩大，当荷载达到2.0×105N时，位于地锚结构左上方的塑性区逐渐向上部土体扩展，塑性区局部贯通至地表，同时右上方也出现了局部的塑性区(见图11(c))；随着荷载的继续增加，当荷载达到2.4×105N时，地锚结构右上方塑性区逐渐扩展贯通(见图11(d))，结合Q-S曲线和塑性区综合判断，此时土体丧失承载能力，地锚结构失效.

图11 不同荷载作用下塑性区分布图

2.3.3 地基滑动面分析

参照相关文献，确定在外荷载作用下地基土体发生破坏后其滑动面位置的判断准则如下[12-14]：地基土体在荷载作用下发生破坏后，滑动面上下土体的位移会产生明显的分界面，且上部土体位移较大，下部土体位移较小.上述条件为判断地锚结构地基土体是否处于极限状态的充分条件，通过观察滑动面附近地基土体的位移变化情况，分析其显著程度，可以判别地基土体是否处于极限平衡状态，进而获得滑动面的位置、范围.锚板基础土体在斜向上拔荷载作用下会发生塑性破坏，通过观察地基土体的塑性区分布是否连续贯通，是判断地基土体是否处于极限平衡状态的必要条件.

一般而言，不同岩土材料，由于其本身的物理力学性质存在着差异，在发生破坏时对应的荷载和位移值并不一致，如文献[15] 通过模型试验观测锚板的上拔过程，当荷载值达到极限时，最大位移量为0.75 mm，但对不同密实度的土体，其结果也会产生差异[6].本文结合上述数值模拟获得的塑性区的发展情况，在出现塑性区的范围内搜索位移矢量趋向基本相同、位移量值相等的位移界面，通过搜索找到位移矢量图中位移为10 mm的等位移界面位移矢量趋势相同，并将该界面确定为滑动面.依据上述滑动面的确定方法，在可以确定不同加载阶段地基土体位移矢量图中滑动面的扩展过程(见图12中各级荷载下白线所描述的滑动面).