卡尔曼滤波方法在地下水污染源反演中的应用

白玉堃,卢文喜*,李久辉

卡尔曼滤波方法在地下水污染源反演中的应用

白玉堃1,2,卢文喜1,2*,李久辉1,2

(1.吉林大学地下水与资源环境教育部重点实验室,吉林 长春 130012；2.吉林大学新能源与环境学院,吉林 长春 130012)

采用卡尔曼滤波方法反演识别地下水污染源的个数和大概位置.借助一个假想算例,建立地下水系统水流和溶质运移模拟模型,利用灵敏度分析方法筛选出对模拟结果影响最大的参数作为随机变量,对该参数进行抽样,运用蒙特卡罗方法将抽样结果输入模拟模型,生成污染质浓度场.采用卡尔曼滤波方法构造迭代过程,逐个利用采样点处浓度的实测值不断更新综合浓度场.引入模糊集理论表示污染羽,对比综合污染羽和单个污染羽的模糊集来更新各潜在污染源的权重,根据潜在污染源权重大小和综合污染羽收敛形状判断真实污染源的个数和大概位置.算例结果表明:采用卡尔曼滤波方法可以成功反演识别出地下水污染中真实污染源的准确个数和大概位置;引入模糊集理论表示污染羽,通过对比综合污染羽和单个污染羽的模糊集,可以确定各潜在污染源的权重.

污染源识别；卡尔曼滤波；模糊集；蒙特卡罗；灵敏度分析

与地表水不同,地下水污染一般具有存在的隐蔽性和发现的滞后性等特点,使人们对地下水污染源的状况缺乏了解,包括污染源的个数、空间位置以及释放历史等.展开对地下水污染源反演识别的研究工作,可以了解地下水污染源的特征,为设计污染修复方案提供决策依据.

地下水污染源反演识别是,根据污染场地的水文地质条件和动态监测数据以及一些专家经验等辅助信息,对描述地下水污染的模拟模型进行反演求解,从而辨识确定含水层中地下水污染源的特征.目前已有的应用于地下水污染源反演识别问题的方法有:地球物理探测法、污染因子分析法以及数理方程反演法[1-3]00,其中又以数理方程反演法应用最为广泛.

卡尔曼滤波法是基于概率统计的一种数理方程反演方法.早先Dokou等[4]以蒙特卡洛随机地下水水流模型和水质模型通过卡尔曼滤波方法反演识别了DNAPL源的最佳位置;之后又在污染源强度未知的三维模型中验证了该方法的可行性[5].江思珉等[6]基于卡尔曼滤波方法和模糊集合理论成功反演识别了污染源的位置;后又结合单纯形法对地下水污染源强度进行了识别[7].为适应不同问题的需要,卡尔曼滤波方法逐渐发展出扩展、集合、无迹卡尔曼滤波等形式,Xu等[8]利用集合卡尔曼滤波方法在一个二维合成确定性含水层中有效的反演识别了污染源的位置、释放时间和初始释放浓度.为了解决反演过程中滤波不稳定或发散问题,崔尚进等[9]通过对常规卡尔曼滤波方程中的协方差矩阵进行U-D分解,增加了该方法的数值稳定性,并用一个二维模型成功反演识别了污染源位置.

已有的地下水污染源反演研究多是借助假想算例反演识别污染源的位置和强度,且算例中真实污染源的个数往往设定为1个, 本文针对同时存在有多个真实污染源的算例问题,采用卡尔曼滤波方法对真实污染源的个数及其大概位置进行识别.另外,在实际问题中,由于地下水系统的复杂性,地下水污染源反演问题往往存在诸多场地信息不确定性,如水文地质参数的不确定性以及由调查数据的误差或缺失引起的不确定性[9-12]00;为表示场地信息的不确定性,已有的研究通常事先确定模型中的某种参数作为随机参数,本文通过对所建立模拟模型中的参数进行灵敏度分析,筛选出灵敏度最高的参数作为随机参数, 其他参数作为确定性参数,使随机参数的选取有据可依.

1 研究方法

1.1 污染源反演识别流程

在现场调查、动态监测和定性分析的基础上,根据研究区的水文地质条件和专家经验,确定污染源可能出现的范围,初步估计污染源存在的位置、个数及每个潜在污染源的初始权重(权重表示该污染源为真实污染源的可能性大小,取值0~1之间).写出地下水污染的水流和溶质运移数学模型的一般表达式,对模型中的各项输入变量均给出经验估计值(包括污染源释放历史),初步建立地下水水流数值模拟模型和溶质运移数值模拟模型.考虑场地信息的不确定性,对输入模拟模型中的参数进行灵敏度分析,筛选出灵敏度最高的参数作为随机变量,其它参数作为确定性变量,根据现场调查和专业经验,对于随机变量给出其取值区间,对于确定性变量给出其具体经验估计值;对于筛选出的随机变量,在其取值区间内采用拉丁超立方方法进行抽样生成参数随机场,运用蒙特卡罗方法将参数随机场输入模拟模型,生成溶质浓度场,结合各潜在污染源的初始权重计算得到初始综合浓度场和初始误差协方差矩阵.根据采样点实测数据,运用卡尔曼滤波更新方程构造合适的迭代过程,对综合浓度场和协方差矩阵进行修正更新,对比用模糊集表示的综合污染羽和各潜在污染源的单个污染羽,运用全局相似度公式,计算各潜在污染源的全局相似度来更新潜在污染源的权重.判断权重是否稳定,若稳定则停止更新,否则选取新的采样点继续更新.污染源反演识别流程见图1.

图1 污染源反演流程

1.2 参数灵敏度分析

灵敏度分析方法有两种,一是局部灵敏度分析,它的特点是只改变某一个参数的值而保持其他参数值不变,在此前提下分析某个参数发生变化时对模拟模型输出结果的影响;二是全局灵敏度分析,它的特点是可以考虑不同参数共同作用对模拟模型输出结果的影响,能够计算出所有参数的总灵敏度[13].

本文运用局部灵敏度分析方法,筛选出对模拟模型影响较大的参数:首先给待分析参数赋值,输入模拟模型并得到输出结果,然后将参数增加和减少一定的幅度并输入模拟模型,可以获得与输入对应的输出结果.运用下式计算出该参数的灵敏度:

在实际问题中可以用下式来近似求得某一特定参数的灵敏度系数:

1.3 拉丁超立方方法

1.4 计算初始综合浓度场和初始误差协方差矩阵

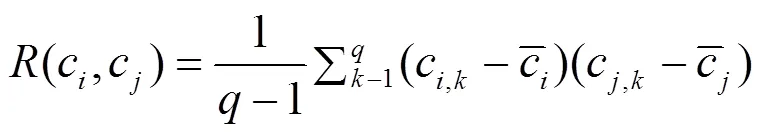
1.5 卡尔曼滤波更新

运用卡尔曼滤波状态更新方程,结合采样点处的浓度值,对综合浓度场和协方差矩阵进行迭代更新,使综合污染羽逐渐向真实污染羽收敛,达到反演识别真实污染源个数及其大概位置的目的.卡尔曼滤波的状态更新方程如下:

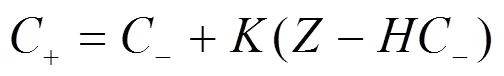
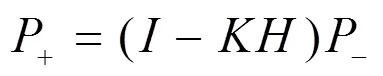
在对初始综合浓度场进行更新时,第一步迭代更新所需要的-和-既是1.4节计算得到的初始误差协方差矩阵和初始综合浓度场.

1.6 潜在污染源权重更新

为了判断潜在污染源是否为真实污染源,每运用卡尔曼滤波方程更新一次综合浓度场,都要计算新的综合污染羽中各潜在污染源的权重大小.引入模糊集表示污染羽,即将综合浓度场和各个潜在污染源的均值浓度场进行标准化(场内各浓度值除以其中浓度最大值),设定4个模糊集标准:

1=0.2,2=0.4,3=0.6,4=0.8

对比各模糊集标准下综合污染羽和单个污染羽的相似度,并计算全局相似度来更新潜在污染源的权重,全局相似度计算公式如下:

式中:as表示某一给定的标准值;Ss表示在某一标准as下的综合污染羽与单个污染羽比较所得两者的重合面积(图2灰色区域);g即是单个污染源的全局相似度.

计算所有潜在污染源的全局相似度后对它们进行标准化(各潜在污染源的全局相似度除以其中最大的全局相似度),标准化后的全局相似度即为新的各潜在污染源的权重.

2 假想模型算例分析

2.1 模型建立

假定一个1000m´1000m大小、含水层厚30m的研究区,含水层非均质各向同性,岩性主要为粗砂,水流为潜水非稳定流,以底板为零基准面,初始水位23m,建立水流模型时将研究区北部边界和南部边界概化为已知水头边界,水头分别为27m(北)、22m(南),东、西两侧概化为隔水边界;忽略蒸发腾散作用,研究区垂向上均匀接受降水入渗补给,年平均降水量为 550mm.研究区内估计存在潜在污染源个数有3个(图3),设定其中1号和2号为真实污染源.将污染质看作为不发生化学转化与生物迁移的保守污染物,污染泄漏量500m3/d,污染泄漏浓度40mg/L;模拟时长为800d;在建立溶质运移模型时将南北两侧的已知水头边界概化为已知浓度边界,东西两侧的隔水边界概化为零通量边界;根据专家经验,给3个潜在污染源赋予初始权重,分别为0.6,0.5, 0.7.

根据水文地质条件,建立地下水水流数学模型:

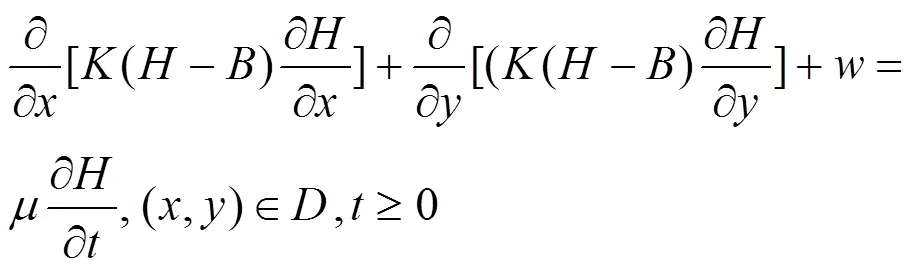
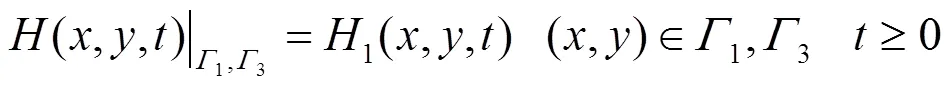
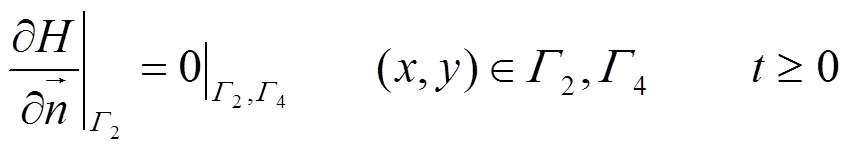
在地下水水流数学模型的基础上,建立地下水溶质运移数学模型:

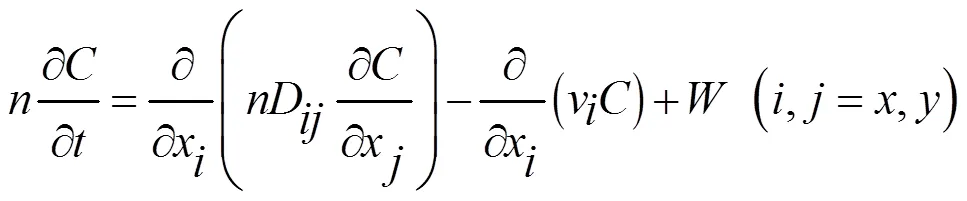
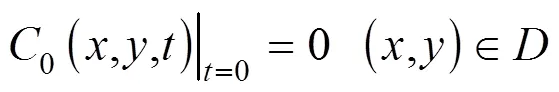
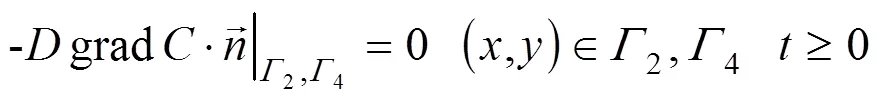
式中:为介质孔隙度,无量纲;为污染质浓度, mg/L;为水动力弥散系数,m2/d;为渗流速度, m/d;表示单位时间单位液相体积内污染质质量的增减量,1,3为已知浓度边界;2,4为零通量边界.

2.2 算例分析

将研究区剖分为10´10的单元网格.运用 GMS中的MODFLOW和MT3DMS工具箱完成研究区的水流和污染质运移模拟.考虑到场地信息的不确定性,运用参数灵敏度分析方法筛选出灵敏度最高的参数作为随机变量,其他参数作为确定性变量输入模拟模型.筛选时先将各参数取均值(表1)输入模拟模型,输出对应的模拟结果,然后将其中的某一个参数加上或减去其均值的10%,20%,其他参数不变输入模拟模型,可以分别得到对应参数取值下的模拟结果.

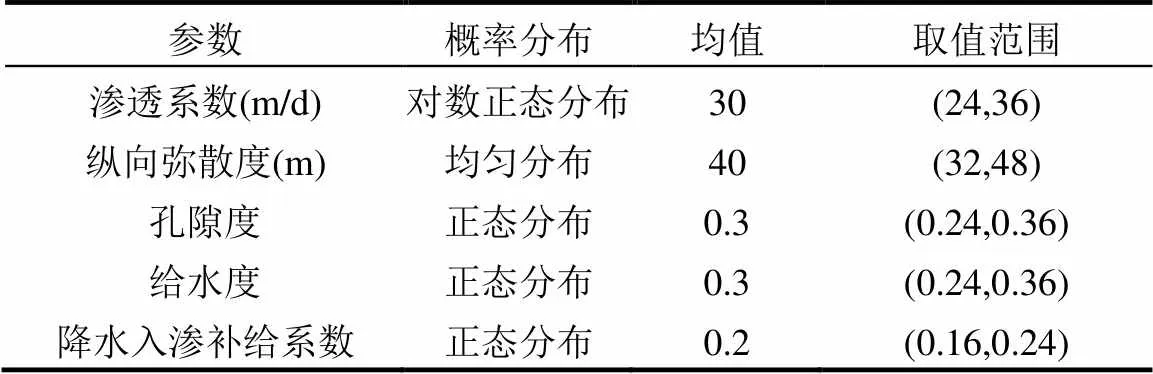
表1 参数的概率分布及取值情况

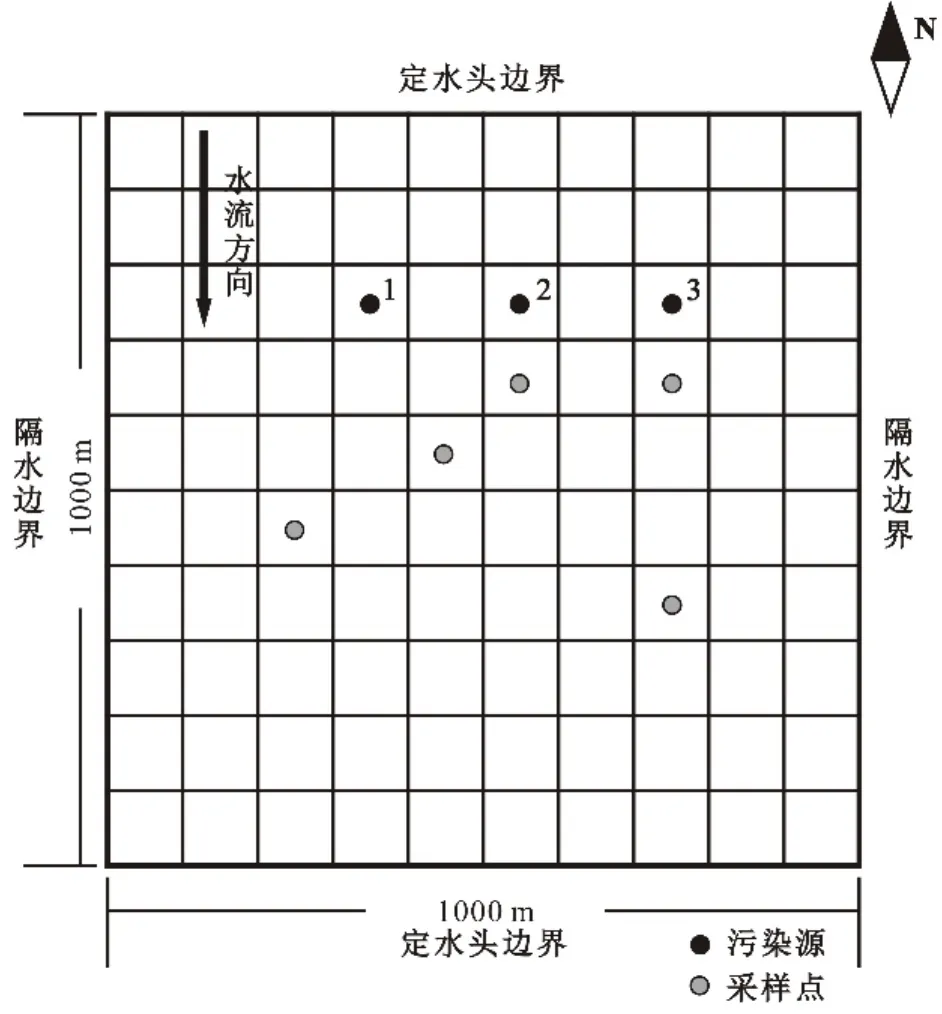
图3 污染场地平面图

利用(2)式计算该参数的灵敏度.同理,计算出所有参数的灵敏度后,对比筛选出灵敏度最高的参数.由图4可以看出,对模型结果影响最大的参数为渗透系数.

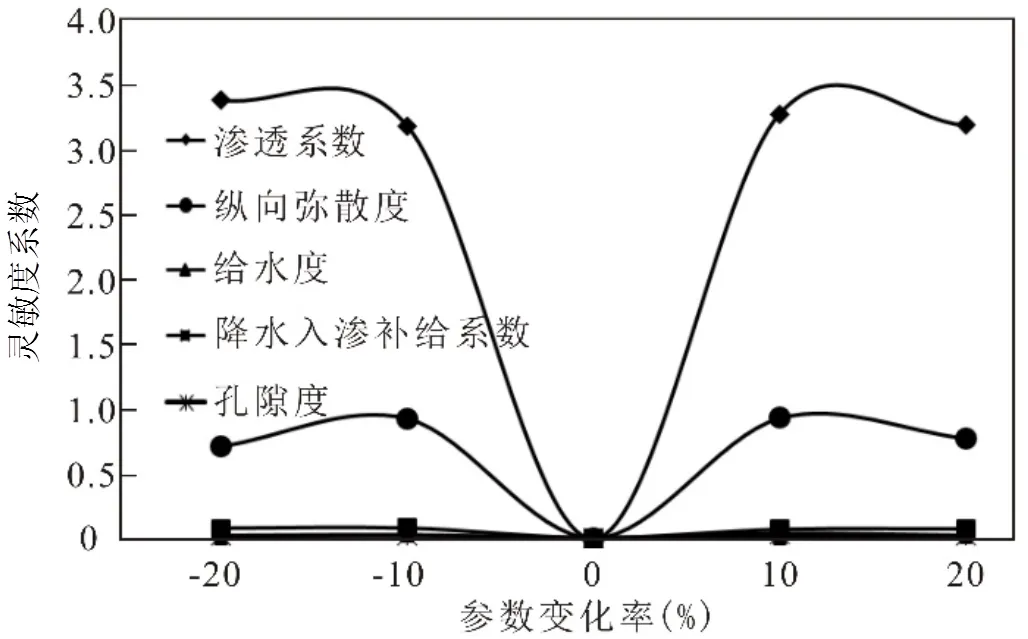
图4 参数灵敏度分析

图5 渗透系数场的某次抽样

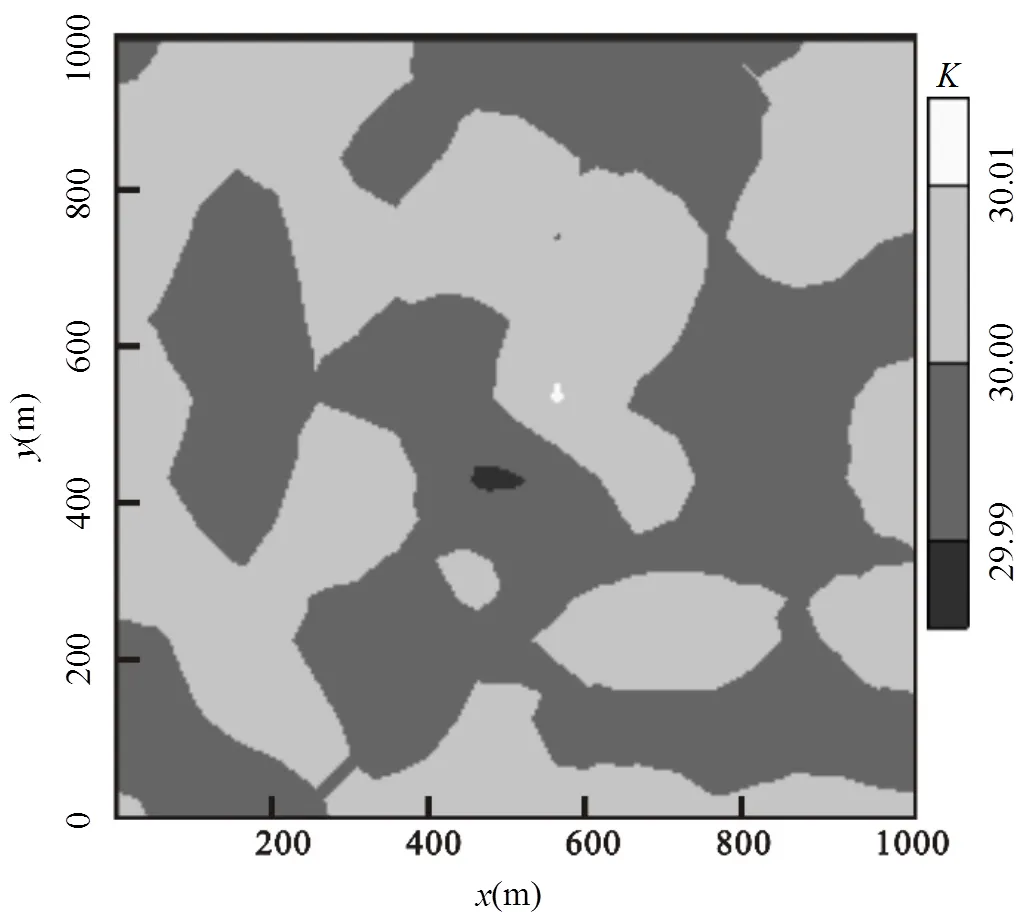
图6 真实渗透系数场

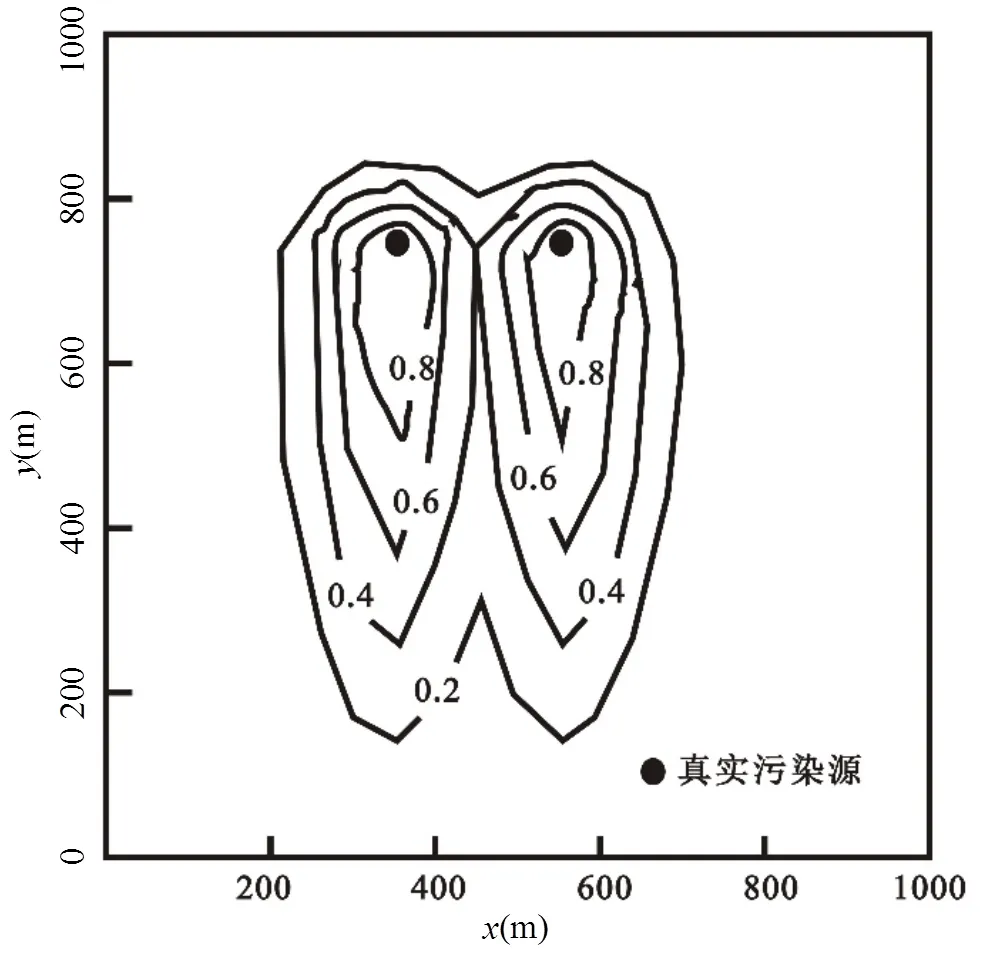
图7 真实污染羽

利用拉丁超立方方法对筛选出的渗透系数进行抽样,本次抽样120次,即得到120个渗透系数随机场,渗透系数场的某次抽样结果见图5.考虑到场地相关性,本文对抽出的渗透系数随机场进行相关性排序[20],将排序后的渗透系数随机场输入模拟模型.图6所示为真实渗透系数场,结合给定的真实污染源信息,输入模型可获得真实污染羽(图7).算例中有3个潜在污染源,结合120个渗透系数随机场可生成3´120个溶质浓度场,在此基础上按照1.4 节表述过程计算得到初始综合浓度场和初始误差协方差矩阵,然后运用卡尔曼滤波状态更新方程更新综合浓度场,图8(a)~8(d)给出综合污染羽的更新结果.

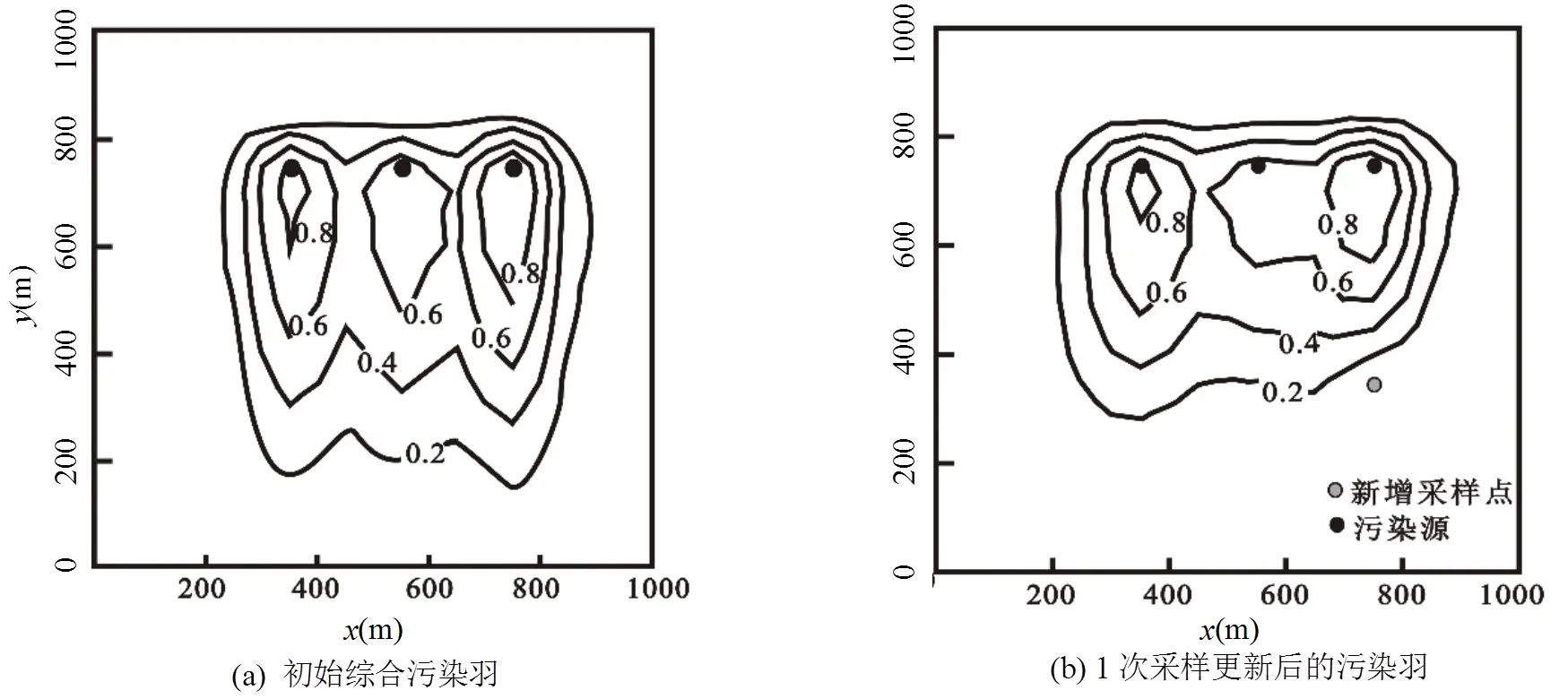
图8(a)所示为未进行更新前的初始综合污染羽,图8(b),(c),(d)分别为利用1个、3个、5个采样点数据更新综合浓度场后的综合污染羽,可以看出,在5次采样更新完成之后综合污染羽不断收敛,最终相似于图7所示的真实污染羽,且3号污染源已被完全排出污染羽范围.图8(e),(f)为更新前后潜在污染源权重分布图,发现1号、2号、3号污染源权重分别由初始的0.6、0.5、0.7经过5次采样更新后变化为0.9、1、0.09.由5次采样更新后的综合污染羽形状以及污染源的权重分布可以判断:3个潜在污染源中1号和2号为真实存在的污染源,研究区内真实污染源个数为2个,且污染羽内浓度最高处即为污染源最可能存在的位置.

3 结论

3.2 对于含有多个真实污染源的反演识别问题,卡尔曼滤波方法仍然适用;本文经过5次采样更新后,准确识别出研究区内真实污染源的个数为2个,且真实污染源的位置最可能在污染羽内浓度最高处.

3.3 本文采用一个含有多个真实污染源的假想算例,旨在展示卡尔曼滤波方法在该情境下的适用性,为减少工作量,研究区网格剖分数目较少,建议在实际应用中适当增加网格剖分数目,以提高采样点数据对网格所表示区域的代表性.

[1] 王景瑞,胡立堂.地下水污染源识别的数学方法研究进展[J]. 水科学进展, 2017,28(6):943-952. Wang J R, Hu L T.Advances in mathematical methods of groundwater pollution source identification [J]. Advances in Water Science, 2017,28(6):943-952.

[2] 董海彪.基于克里格替代模型和改进的Bayesian-MCMC方法的地下水污染源反演识别研究[D]. 长春:吉林大学, 2016. Identification of groundwater pollution sources based on kriging alternative model and improved Bayesian-MCMC methods [D]. Changchun: Jilin University, 2016.

[3] Milnes E, Perrochet P. Simultaneous identification of a single pollution point-source location and contamination time under known flow field conditions [J]. Advances in Water Resources, 2007,30(12):2439-2446.

[4] Dokou Z, Pinder G F. Optimal search strategy for the definition of a DNAPL source [J]. Journal of Hydrology, 2009,376(3):542-556.

[5] Dokou Z, Pinder G F. Extension and field application of an integrated DNAPL source identification algorithm that utilizes stochastic modeling and a Kalman filter [J]. Journal of Hydrology, 2011,398(3):277-291.

[6] 江思珉,张亚力,周念清,等.基于卡尔曼滤波和模糊集的地下水污染羽识别[J]. 同济大学学报(自然科学版), 2014(3):435-440.Jiang S M, Zhang Y L, Zhou N Q, et al.Groundwater contaminant plume identification by using Kalman filter technique and fuzzy set theory [J].Journal of Tongji University (Natural Science), 2014(3):435-440.

[7] 江思珉,张亚力,周念清,等.基于污染羽形态对比的地下水污染源识别研究[J]. 水利学报, 2014,45(6):735-741.Jiang S M, Zhang Y L, Zhou N Q, et al.Groundwater contaminant source identification based on the morphological comparison of pollution plume [J].Journal of Hydraulic Engineering, 2014,45(6):735-741.

[8] Xu T, G MEZ-HERN NDEZ J J. Joint identification of contaminant source location, initial release time and initial solute concentration in an aquifer via ensemble Kalman filtering: Identification of a contaminant source [J]. Water Resources Research, 2016,52(8):6587-6595.

[9] 崔尚进,卢文喜,顾文龙,等.基于U-D分解的卡尔曼滤波法在地下水污染源识别中的应用[J]. 中国环境科学, 2016,36(9):2633-2637. Cui S J, Lu W X, Gu W L, et al.Application of U-D factorization- based Kalman filter to identify the groundwater pollution source [J]. China Environmental Science, 2016,36(9):2633-2637.

[10] 施小清,吴吉春,吴剑锋,等.多个相关随机参数的空间变异性对溶质运移的影响[J]. 水科学进展, 2012,23(4):509-515. Shi X Q, Wu J C, Wu J F, et al.Effects of the heterogeneity of multiple correlated random parameters on solute transport [J]. Advances in Water Science, 2012,23(4):509-515.

[11] 李久辉,卢文喜,常振波,等.基于不确定性分析的地下水污染超标风险预警[J]. 中国环境科学, 2017,37(6):2270-2277. Li J H, Lu W X, Chang Z B, et al.Risk prediction of groundwater pollution based on uncertainty analysis [J]. China Environmental Science, 2017,37(6):2270-2277.

[12] 束龙仓,朱元生.地下水资源评价中的不确定性因素分析[J]. 水文地质工程地质, 2000,27(6):6-8.Shu L C, Zhu Y S.Analysis of uncertainties in groundwater resource evaluation [J].Hydrogeology and Engineering Geology, 2000,27(6):6-8.

[13] 束龙仓,王茂枚,刘瑞国,等.地下水数值模拟中的参数灵敏度分析[J]. 河海大学学报(自然科学版), 2007,35(5):491-495. Shu L C, Wang M M, Liu R G, et al.Sensitivity analysis of parameters in numerical simulation of groundwater [J]. Journal of Hohai University (Natural Sciences), 2007,35(5):491-495.

[14] Mckay M D, Beckman R J, Conover W J. A comparison of three methods for selecting values of input variables in the analysis of output from a computer code [J]. Technometrics, 2000,42(1):55-61.

[15] Rajabi M M, Ataie-Ashtiani B, Janssen H. Efficiency enhancement of optimized Latin hypercube sampling strategies: Application to Monte Carlo uncertainty analysis and meta-modeling [J]. Advances in Water Resources, 2015,76:127-139.

[16] Helton J C, Davis F J. Latin hypercube sampling and the propagation of uncertainty in analyses of complex systems [J]. Reliability Engineering & System Safety, 2003,81(1):23-69.

[17] 尹增谦,管景峰,张晓宏,等.蒙特卡罗方法及应用[J]. 物理与工程, 2002,12(3):45-49. Yin Z Q, Guan J F, Zhang X H, et al. The Monte Carlo method and its application [J].Physics and Engineering, 2002,12(3):45-49.

[18] Densmore J D, Urbatsch T J, Evans T M, et al. A hybrid transport- diffusion method for Monte Carlo radiative-transfer simulations [J]. Journal of Computational Physics, 2007,222(2):485-503.

[19] Herrera G S, Pinder G F. Space-time optimization of groundwater quality sampling networks [J]. Water Resources Research, 2005, 41(12):410-411.

[20] Zhang Y Q, Pinder G. Latin hypercube lattice sample selection strategy for correlated random hydraulic conductivity fields [J]. Water Resources Research, 2003,39(8):472-477.

Application of Kalman filter to identify the groundwater contaminant sources.

BAI Yu-kun1,2, LU Wen-xi1,2*, LI Jiu-hui1,2

(1.Key Laboratory of Groundwater Resources and Environment Ministry of Education, Jilin University, Changchun 130012, China；2.College of Environment and Resources, Jilin University, Changchun 130012, China)., 2019,39(8)：3450~3456

Kalman filter was used to identify the number and approximate location of groundwater contaminant sources. Based on a hypothetical example, a groundwater flow and transport simulation model was established. The parameter that had the greatest impact on the simulation results was selected as a random variable by sensitivity analysis method. Then it was sampled and the sampling results were input into the simulation model by Monte Carlo method to generate the contaminant concentration field. Kalman filter method was used to update the composite concentration field one by one by using the measured concentration values at the sampling point. The fuzzy set theory was introduced to represent the pollution plume, and the weight of each potential contaminant source was updated by comparing the fuzzy sets of composite plume and individual plume. The number and approximate location of the real contaminant sources were judged according to the weight of potential contaminant sources and the convergence shape of composite plume. The results showed that the Kalman filter method can successfully identify the exact number and approximate location of the real contaminant sources in groundwater pollution; the fuzzy set theory was introduced to represent the pollution plume, and the weight of each potential contaminant source can be determined by comparing the fuzzy sets of the composite plume and the individual plume.

contaminant sources identification；Kalman filter；fuzzy set；Monte Carlo；sensitivity analysis

X523

A

1000-6923(2019)08-3450-07

白玉堃(1995-),男,吉林大学硕士研究生,主要从事地下水污染源反演识别问题方面的研究

2018-12-27

国家自然科学基金资助项目(41672232)

* 责任作者, 教授, luwenxi@jlu.edu.cn