典型耦合优化算法在源项反演中的对比研究

沈泽亚,郎建垒,程水源,毛书帅,崔继宪

典型耦合优化算法在源项反演中的对比研究

沈泽亚,郎建垒,程水源*,毛书帅,崔继宪

(北京工业大学,区域大气复合污染防治北京市重点实验室,北京 100124)

突发大气污染事故中,污染源的快速、准确确定是应急处置的基础.为研究有效的源项评估方法,本文基于美国草原外场SO2释放实验,利用GA-PSO、GA-NM、PSO-NM 3种耦合算法,分别与高斯点源烟羽扩散模型结合,对源强和位置等污染源参数进行反演与对比,并从算法结构与大气扩散条件方面进行反演效果差异分析.结果表明,从源强反演角度看,PSO-NM反演结果的准确性最高、稳定性最强,平均误差(11.3%)与平均标准偏差(0.7g/s)明显低于GA-NM(16.4%、13.3g/s)与GA-PSO(29.0%、26.6g/s).从位置反演角度看,PSO-NM的反演结果最为稳定,反演的平均标准偏差(0.29m)明显低于GA-NM(3.20m)与GA-PSO(3.03m)算法;在不稳定和中性扩散条件下,PSO-NM算法的位置反演准确性最高,误差为4.97m;但在稳定扩散条件下,GA-NM的位置反演误差(7.69m)最小.从反演效率角度看,PSO-NM与GA-NM反演时间最短,更适用于污染源的快速确定.

耦合算法；4维源参数；高斯点源烟羽扩散模型；源项反演；突发大气污染事故

突发大气污染事故具有发生突然、形式多样、危害严重的特点[1], 快速、准确确定事故源的排放信息(源强、位置等)是准确、快速应急预警的前提.与常规大气污染源相比,突发大气污染事故源强、位置等信息不确定性很大,很难直接获取,基于监测数据的优化反演是获得源参数的重要途径.目前一些学者已经开展了源反演技术方面的研究.Keats等[2]和Senocak等[3]运用马尔科夫链-蒙特卡洛抽样的贝叶斯推理方法对泄漏源进行了反算.Akcelik等[4]根据扩散方程建立了源强直接优化求解的方法,但是这种方法对初值依赖性较大.张建文等[5]基于虚拟案例发现,混合遗传-Nelder Mead 单纯形耦合算法对源参数(,,)反算效果优于单一的遗传和单纯形算法.Ma等[6]发现吉洪诺夫与粒子群耦合算法潜在危险气体源参数反演的方法,但目前尚不能投入使用.Thomson等[7]发现模拟退火算法和随机搜索算法对源强反算具有良好的鲁棒性.苏芳等[8]利用拉格朗日逆向轨迹反演模式对甲烷排放清单进行反算,发现其不确定性(20~100%)较为可信.李航等[9]利用逆推算法对日本福岛核事故源强进行了反算,发现该计算方法对于紧急条件下无法对事故源强进行近距离评估的情况具有优越性和参考性.吕兆丰等[10]利用地面浓度反推法对某炼油厂VOCs源强进行反算,得出的年排放量结果(2201.6±1011.9t/a)偏低.可见,大部分的研究针对某种算法(如PSO、SA等)对某些参数(如源强或地面位置等)的反演开展了分析,但缺乏不同反演技术对源排放参数反演性能的系统研究对比.

本文在前期系统调研基础上,筛选出了3种典型的、先进的智能优化耦合算法(GA-PSO、GA- NM、PSO-NM)对四维源参数(0,0,0,0)进行了反演研究,并从准确性、稳定性、时效性等方面进行了系统对比分析.本文目的在于,通过对典型耦合优化算法反演多维源参数的系统对比研究,从算法结构和大气扩散条件角度进行反演结果差异分析,筛选出适用于突发大气污染事故的快速、准确的溯源方法,为源项信息的快速确定与突发大气污染事故的合理应对提供思路和技术支持.

1 材料3和方法

1.1 算法介绍

1.1.1 基本算法介绍 选取遗传算法、粒子群算法和单纯形算法3种基本寻优算法,开展两两耦合算法对比研究.标准遗传算法(GA)是模拟自然界生物进化过程的计算模型[11],经过选择、交叉和变异3种基本遗传操作,逼近问题最优解.标准粒子群算法(PSO)的思想源于自然界鸟群捕食和鱼群捕食的过程,通过群体协作找到问题的全局最优解[12].标准单纯形算法(NM)是应用规则或不规则的几何图形,通过反射、扩张、压缩、及整体收缩操作不断构成新的单纯形,最后逼近最优解[13].

1.1.2 遗传与粒子群算法耦合(GA-PSO) 以PSO算法为主体,引入遗传算法中的选择、交叉、变异基本操作,构成新的GA-PSO算法[14].耦合算法中3种遗传操作均用实值编码,满足判定条件或达到最大迭代数后输出最优解.已有研究表明[15-16],GA-PSO耦合算法寻优效果均优于GA和PSO算法.因此本文选用GA-PSO耦合算法在源项反演中开展对比研究.

1.1.3 遗传与单纯形算法耦合(GA-NM) 以GA算法为主体,采用群体分类的方式构建GA-NM耦合算法[17].将群体分为3类,最优群体、最差群体和普通群体,最优群体运行NM算法,最差群体执行重组交叉操作,普通群体执行遗传操作.已有研究[18-19]表明,耦合算法GA-NM的寻优效果均优于GA和NM算法.因此本文选用GA-NM耦合算法在源项反演中开展对比研究.

1.1.4 粒子群与单纯形算法耦合(PSO-NM) 以PSO算法为主体,引入NM 算法构成PSO-NM耦合算法[20].在PSO算法执行达到一定迭代数后,再执行NM算法寻优,直到满足收敛条件.已有研究[21-22]表明,PSO-NM算法在计算均值与成功率等方面较PSO和NM算法更有优势.因此本文选用 PSO-NM耦合算法在源强反演中开展对比研究.

1.2 反算模型的构建

1.2.1 高斯模型 在连续气相泄漏的源强反算模型中,正向采用高斯烟羽扩散模型[23]来模拟连续气相泄漏源的扩散浓度,在高斯模型中,以风向为轴,侧风向为轴建立坐标系,高斯模型的表达式如下:

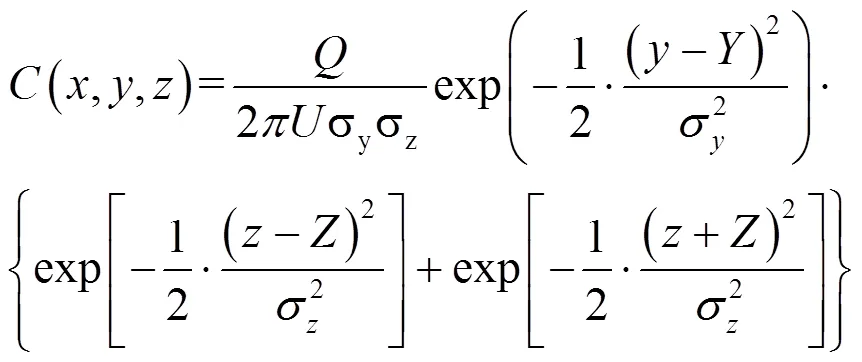
式中:(,,)为监测点在(,,)位置处的污染物浓度,g/m3;为平均风速,m/s;为水平扩散参数,m;为垂直扩散参数,m;为释放源强,g/s;为释放源点的纵坐标,m;为释放源点的距地面垂直高度,m.

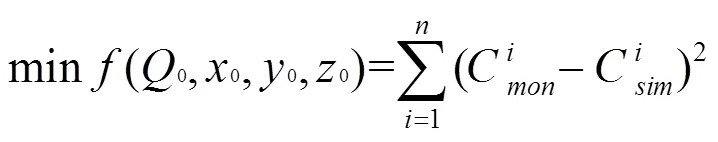
式中:y、z分别表示第个监测点的坐标和采样高度,m.0反演源的源强,g/s.0、0、0分别为反演源的位置坐标,m.将(3)式作为耦合优化算法中的适应度函数,进行寻优求解.

通过编程计算,将(3)式作为耦合优化算法的适应度函数,最大迭代次数设为1000次,运行过程中判定是否满足收敛条件,满足则运行结束,输出结果,否则算法继续迭代优化,直至满足收敛条件. Zhang等[24]研究表明,启发式优化算法在寻优过程中容易受到初始值的影响,可通过增加运行次数的方式有效降低其影响.Cantelli等[25]和Cervone等[26]研究中应用遗传算法寻优的运行次数为30、300次,本研究运行次数为3000次,并保证在同一运算环境下开展源项反算研究.

1.3 经典实验介绍

1956年夏季,在美国内布拉斯加州中北部奥尼尔镇(北纬40°29.6’,西经98°34.3’)开展了草原SO2气体释放外场实验[27],实验场地海拔高度约600m,地处奥尼尔镇北部,距离镇中心约8000m.试验场地属于近水平高地,为草原地形,地势平坦.实验涉及多种大气扩散条件,采用Pasquill分类方法,总体上大致可分为不稳定、中性和稳定3种条件.不稳定条件下的实验在白天开展,由于晚上没有阳光,大气扩散相对稳定,故大部分中性和稳定条件的实验在傍晚或者夜间开展.实验以释放源点为中心,分别以50、100、200和400m为半径,由西向东、顺时针、半圆弧布设监测点,相邻监测点的间隔为2°,每一圆弧布点编号为1~91#,源正西方向监测点编号为1#,正东方向为91#,布点简图如图1所示.监测点高度距地面1.5m.

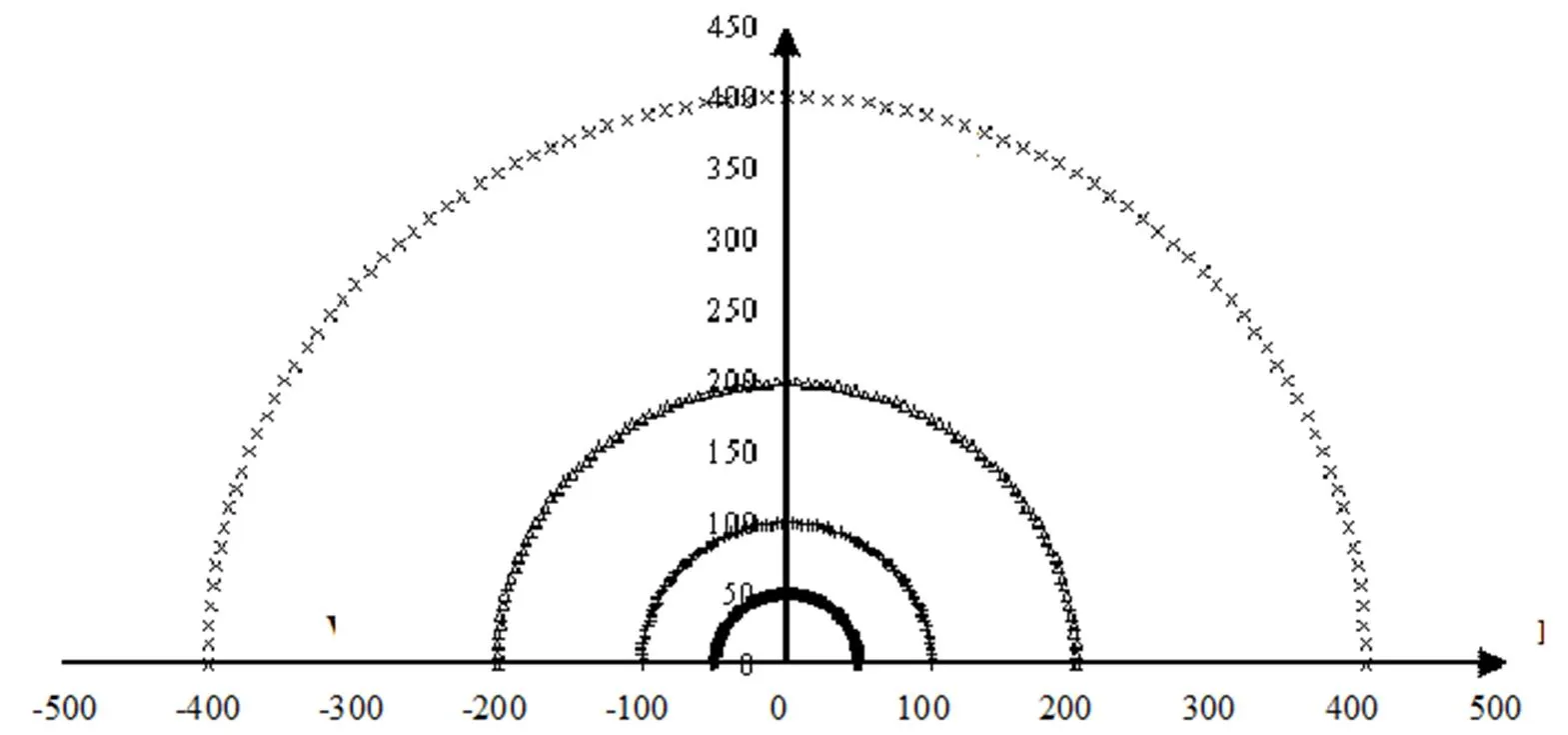
图1 经典实验布点方式

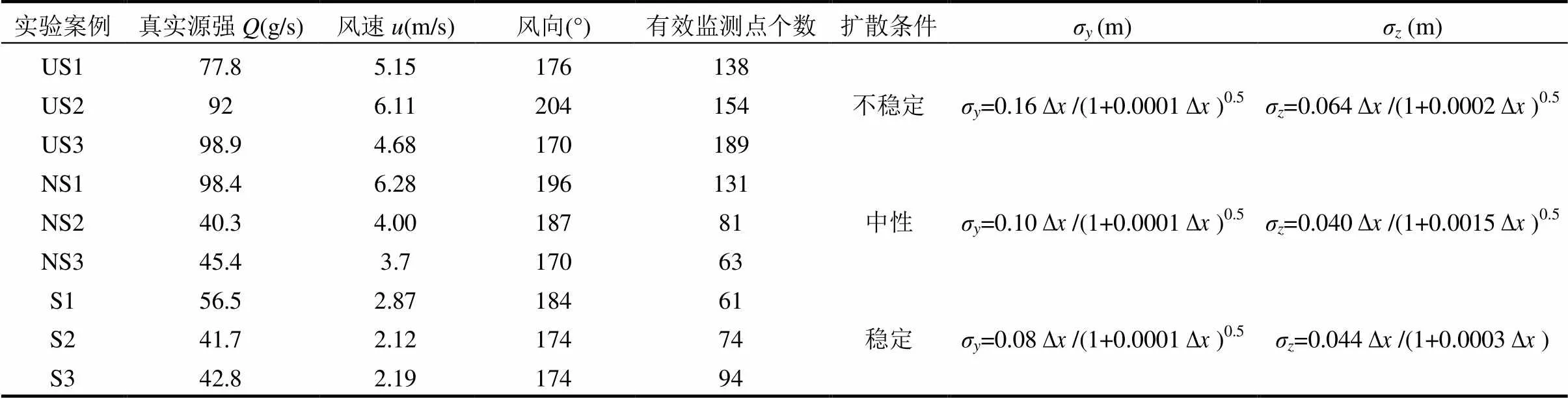
表1 实验开展条件及扩散参数

注:Δ=-0,即采样点位置的横坐标与反演源横坐标之差.

本文在不稳定、中性和稳定3种大气扩散条件下各选取3次实验开展源项反演研究,实验编号记为US1、US2、US3、NS1、NS2、NS3、S1、S2、S3.释放源高度均为0.46m,其他实验参数及σ和σ扩散参数[28]见表1,其中有效监测点个数为实际能够监测到SO2浓度的所有点位个数.本文以释放源为坐标原点,风向为轴,风向逆时针旋转90°为轴,高度为轴建立坐标系,利用高斯扩散模型模拟下风向各监测点浓度.本研究真实源强记为,坐标记为、、,其中=0m、=0m、=0.46m,对应的反演源的源强和位置坐标记为0,0,0,0.

2 结果与讨论

2.1 正向扩散模拟评估

高斯扩散模型模拟结果如图2所示,9次实验的模拟值与监测值均有较好的相关性,均达到0.9以上,利用高斯点源烟羽扩散模型的模拟结果与监测结果的相关系数均大于0.9;从统计学的角度分析,模拟结果与监测结果两组数据的值明显小于0.05,相关关系十分显著,同时证明了值是可信的.但是模拟结果与监测结果仍存在一定的误差,其不确定性主要来源于两方面:一是SO2浓度的监测存在不可避免的误差,二是由于高斯模型本身的限制,模拟时未考虑地形及气象条件的影响.因此,在不同的稳定条件下,高斯点源烟羽扩散模型均适用于点源扩散模拟,验证了扩散系数σ、σ(表1)对本实验模拟是适用的,同时高斯点源烟羽扩散模型及9次实验均为源强反演中目标函数的构建提供良好的支撑.

2.2 反向反算结果

根据已有研究成果[29],不同的监测点数量对源强反演效果存在一定影响,发现增加监测点数可以减小反演结果的误差,但增加到25个监测点时,再增加监测点数量,反演结果几乎无变化.因此,本文为了减小源强反算的误差,按照监测值与模拟值误差的绝对值小于0.005g/m3的原则选取监测点,进行源参数反算.

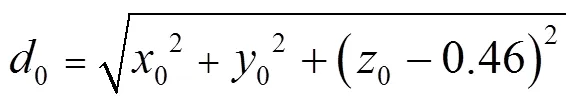
图3 不同算法的反演结果比较

2.3 反算结果分析

2.3.1 源强反算结果分析 图3a显示,综合分析9次实验的源强反演结果发现,PSO-NM算法的反演结果与真值最为接近,准确性更高,平均误差为11.3%;GA-NM算法的反演准确性次之,平均误差为16.4%;GA-PSO算法的反演准确性最差,平均误差为29.0%.在不稳定条件和中性条件下,3种算法的反演准确性与9次综合反演结果类似,均为PSO-NM最高(9.5%)、GA-NM次之(22.3%)、GA-PSO最低(32.9%).而在稳定条件下(S1、S2、S3)不同,GA-NM算法的准确性最高,平均误差为4.6%;PSO-NM算法次之,平均误差为15.0%;GA- PSO算法最差,平均误差为21.2%.因此,从源强反演的准确性角度分析,在大气扩散条件为不稳定和中性下,优先考虑使用PSO-NM算法;大气扩散稳定条件下,优先考虑选用GA-NM算法开展源强反算研究.

从源强反演结果的稳定性来看,在9次实验与各大气扩散条件(不稳定、中性、稳定)下,PSO-NM算法源强反演结果的标准偏差为0.0~2.2g/s,平均标准偏差为0.7g/s;GA-NM算法源强反演结果的标准偏差为8.8~18.5g/s,平均标准偏差为13.3g/s;GA- PSO的源强反演结果的标准偏差为22.3~32.9g/s,平均标准偏差为26.6g/s.通过对比分析可以发现,PSO-NM源强反演的标准偏差范围与平均标准偏差均明显低于GA-NM与GA-PSO,稳定性最强.因此,从算法稳定性来看,不同大气扩散条件下PSO-NM算法的反演结果最为稳定,建议在源强反算研究中优先选用.

2.3.2 位置反算结果分析 图3b-e给出了坐标及距离反算的均值及标准偏差结果,图4给出了不同算法坐标反演及距离计算误差的结果.从反演源与真实源之间的距离考虑,如图4a,在大气扩散不稳定(US1、US2、US3)和中性(NS1、NS2、NS3)条件下,从算法反演准确性角度看,PSO-NM算法反演结果的平均误差(4.97m)最小,GA-PSO(8.41m)次之, GA-NM(8.49m)最大,表明PSO-NM 算法的反演源与真实源的距离最小,更加接近真实源排放位置,在距离反算中优先选用PSO-NM算法.而在稳定条件(S1、S2、S3)下,GA-NM算法的平均误差(7.69m)最小,GA-PSO(8.15m)次之,PSO-NM算法(10.98m)最差,因此应优先考虑使用GA-NM算法在稳定条件下的距离反演.图4c~d的结果表明,从对0和0坐标的反演结果来看,结果与0相似.9次实验中, PSO-NM算法反算的平均误差(1.21m)普遍小于其他两种算法(4.54、4.7m),表明在3种大气扩散条件下,PSO-NM算法对0和0反演时的准确度普遍较高,此时优先使用PSO-NM算法.图4a显示,从0坐标反演的准确性角度考虑,不稳定条件下,PSO-NM算法的反算的平均误差(2.98m)小于其他两种算法(5.29、5.15m),证明当大气处于不稳定扩散条件下时, PSO-NM算法的准确性最高,应优先使用PSO-NM算法开展源反算研究;而在大气扩散条件为中性和稳定时,GA-PSO算法反演结果的平均误差(4.93m)与GA-NM算法(4.99m)接近,且明显低于PSO-NM算法(8.45m),此时应优先考虑选用GA-PSO算法或者GA-NM算法.

从图3b~e中可以看出,9次实验中,在对不同位置参数(0、0、0、0)进行反算时,PSO-NM算法的标准偏差均最小.反演结果中,PSO-NM算法对位置反演的标准偏差范围及平均标准偏差均最低,分别为0.11~0.54m、0.29m;GA-NM算法(2.93~4.75m、3.20m)与GA-PSO算法(2.95~4.33m、3.03m)则相差不大.因此,从算法的稳定性角度考虑,3种大气扩散条件下,PSO-NM算法对位置参数反演最为稳定,与只考虑源强反算时的结果保持一致.

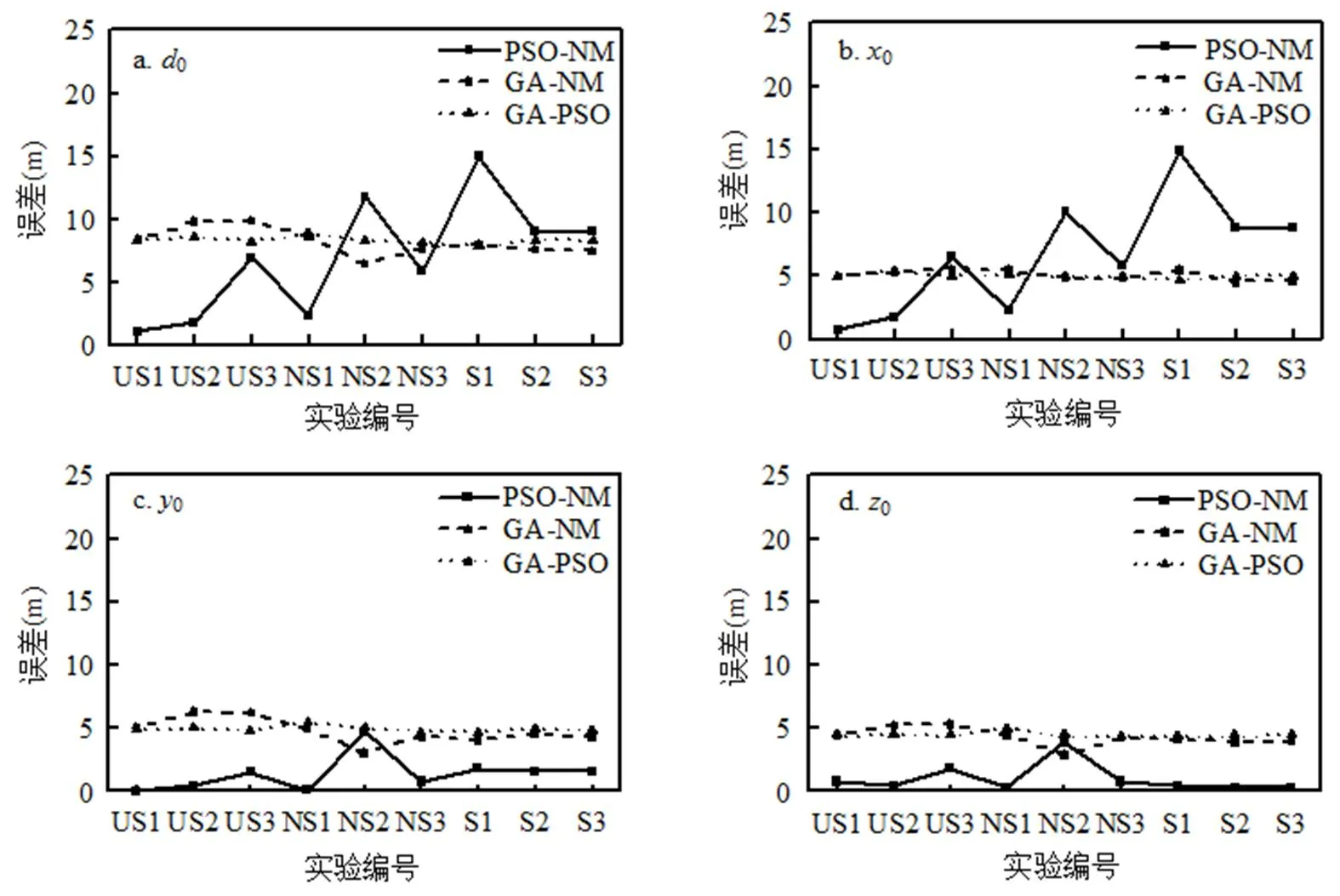
图4 不同算法坐标反演及距离计算误差结果

2.3.3 反算时间结果分析 图3f给出了反算时间结果,整体上来看,PSO-NM算法的平均反算时间(1.65s)与GA-NM算法(1.57s)接近,且明显快于GA-PSO算法(12.46s),这可能与算法本身固有的结构有关.图3f显示,在PSO-NM算法与GA-NM算法在不同大气扩散条件下的时间变化趋势大致相同,GA-NM算法略快于PSO-NM,且两者的反演时间不超过7s,且在大气扩散中性和稳定条件下,两种算法反演时间在1s左右.而GA-PSO算法的反算时间范围为10s~17s,且只有在稳定条件下对源参数进行反算时,3种算法的反演时间变化不大.综上所述,在反演时间方面,GA-NM的用时最短,效率最高,可应用于快速应急处置.

2.3.4 算法结构分析 首先图3a~d显示,整体上PSO-NM算法对源参数(0、0、0、0)反演的准确性要高于其他算法,与算法本身结构有直接关系.标准GA和PSO算法局部收敛性能较差,更有利于全局收敛.同时GA算法采用二进制编码,并以概率的方式进行3种基本遗传操作(选择、交叉、变异),导致准确度较差.相反PSO算法,以既定的规则寻求最优解,并赋予记忆功能,使得寻优过程中范围不断缩小,从而逼近最优解,因此其准确性高于GA算法.不同的是,NM算法收敛速度快,稳定性强,多次寻优不会出现很大的偏差,其最大的局限性是受局部最优值数量的影响较大,容易导致局部收敛,准确度难以保证.图3f中GA-NM和PSO-NM算法的运行时间明显快于GA-PSO算法,这是由于GA和PSO算法均不能快速局部收敛,故需要消耗更多的时间寻优.其次,从反算的稳定性角度来看,PSO-NM算法的稳定性最高.这可能是因为相对于以概率方式寻优的GA算法,以既定规则寻优的PSO算法在进行多次反算时,稳定性要高于GA算法.因此,PSO-NM耦合算法的稳定性能优于其他两种耦合算法.

从初值产生方式看,PSO-NM算法加入了单纯形算法,对初值做了优化,而GA-NM和GA-PSO算法以随机的方式产生初值,具有很大的不确定性.从内部耦合结构看,PSO-NM算法是先利用PSO算法进行寻优,到一定的迭代数后,采用单纯形法加速收敛,既能节省时间又可提高准确率.GA-NM算法采用群体分类的方式进行耦合,运行过程中最优群体中的个体不易与其他群体中的个体发生重组,导致局部收敛.GA-PSO算是在PSO算法中引入了基本遗传操作,计算量增大,耗时长且不易于局部收敛.从算法本质出发,综合准确性、稳定性及运行时间因素,PSO-NM算法对源项参数反演效果整体上优于其他两种算法的结果是科学、合理的.

2.3.5 大气扩散条件分析 图3a中,GA-NM算法和GA-PSO算法对源位置反演时,不同稳定度下反演误差整体上变化不是很明显,因此2种算法在对位置反演时受稳定度影响不大.以PSO-NM算法对源强0反演为例,不稳定条件下的误差最小(8.2%),中性条件下次之(10.9%)、不稳定条件下误差最大(15.0%).在不稳定条件下,从表1中可以看出,有效监测点位数量最多,平均160个左右,这可能是由于实验在白天开展时受到太阳辐射的影响,风向风速变化较为明显,导致污染物扩散烟羽的覆盖范围变大[26],而在稳定条件下时,有效监测点位数量明显变少,平均76个左右,这可能是由于实验在夜间开展,风向风速较为稳定,污染物扩散烟羽的覆盖范围较小.因此按照2.2节中的条件筛选用于反算的监测点时,虽然数据量相差不大,但选取的监测点范围却存在差异,不稳定条件选取的监测点数据覆盖范围最大、中性条件次之、稳定条件最小.因此,PSO-NM算法在对源强反算时也可能受到不同大气扩散条件的影响.图3a中显示, PSO-NM算法在不稳定条件、中性条件和稳定条件下的标准偏差分别为0.3,1.4,0.6g/s; GA-NM算法为17.9,12.0,10.1g/s;GA-PSO算法为28.8,25.3,25.7g/s. PSO-NM 和GA-PSO算法的标准偏差变化不大,最大相差3.5g/s.因此PSO-NM和GA-PSO算法受不同大气扩散条件影响不明显.随着大气扩散条件越稳定, GA-NM算法的标准偏差越小,表明GA-NM算法反算的稳定性受到不同大气扩散条件的影响.从时间方面看, PSO-NM算法在不稳定条件、中性条件和稳定条件下为2.65,1.21, 1.09s;GA-NM算法为3.02,0.84,0.83s;GA-PSO算法为13.29,13.18,10.9s.结果表明大气扩散条件越稳定,算法的反算时间越短.

本文主要从源参数反演的准确性、稳定性和反演时间角度,对比分析了不同耦合优化算法的适用性,以为突发大气污染事故的快速应急提供技术参考.算法的优劣直接影响源强反算效果,在未来的研究中可通过优化算法内部结构参数,提升其在源项反演中的性能,并基于真实突发大气污染事故案例对其验证.除优化算法外,监测结果与模型模拟的准确性对反演结果也有较大影响.虽然本研究中高斯模型模拟效果是可接受的,但模拟值与监测值仍存在一定的误差,随着科技的发展,通过先进的监测手段可减小监测误差,提高监测结果的准确性.同时可进一步优化模型扩散参数,提升模型模拟性能,进而改善源参数反演准确性.

3 结论

3.1 从准确性角度来看,PSO-NM算法对0,0,0的反演效果(误差为11.3%,1.21m)最好,GA-NM和GA-PSO算法对0坐标反演效果普遍较好.这可能与不同的算法结构及大气扩散条件有关.

3.2 从稳定性角度来看,PSO-NM算法对源参数(0,0,0,0)反演的稳定性(标准偏差为0.7g/s,0.29m)最好;GA-NM算法源强反演的稳定性优于GA-PSO算法,但GA-PSO对位置反演时稳定性与GA-NM算法相近.

3.3 从反演时间方面来看,PSO-NM算法(1.65s)与GA-NM算法(1.57s)在源参数反演过程中用时短,效率高.同时大气扩散条件越稳定,算法的反演时间越快.

[1] 唐仙丽,杨宇静.论中国突发性环境污染事故应急立法的完善[J]. 重庆大学学报(社会科学版), 2005,11(6):114-117. Tang X L, Yang Y J. Improvement of emergency legislation of accidental pollution in China [J]. Journal of ChongQing University (Social Science Edition), 2005,11(6):114-117.

[2] Andrew Keats E Y F L. Bayesian inference for source determination with applications to a complex urban environment [J]. Atmospheric Environment, 2007,41:465-479.

[3] Inanc Senocak N W H M. Stochastic event reconstruction of atmospheric contaminant dispersion using Bayesian inference [J]. Atmospheric Environment, 2008,42(33):7718-7727.

[4] Akçelik V, Biros G, Ghattas O, et al. A variational finite element method for source inversion for convective–diffusive transport [J]. Finite Elements in Analysis & Design, 2003,39(8):683-705.

[5] 张建文,王煜薇,郑小平,等.基于混合遗传-Nelder Mead单纯形算法的源强及位置反算[J]. 系统工程理论与实践, 2011,31(8):1581-1587.Zhang J W, Wang Y W, Zheng X P, et al. Back-calculation of source strength and position by a hybrid genetic-Nelder Mead simplex algorithm [J]. System Engineering-Theory & Practice, 2011,31(8):1581-1587.

[6] Ma D, Tan W, Zhang Z, et al. Parameter identification for continuous point emission source based on Tikhonov regularization method coupled with particle swarm optimization algorithm [J]. Journal of Hazardous Materials, 2017,325:239-250.

[7] Thomson L C, Hirst B, Gibson G, et al. An improved algorithm for locating a gas source using inverse methods [J]. Atmospheric Environment, 2007,41(6):1128-1134.

[8] 苏 芳,邵 敏,蔡旭辉,等.利用逆向轨迹反演模式估算北京地区甲烷源强[J]. 环境科学学报, 2002,22(5):586-591. Su F, Shao M, Cai X H, et al. Estimation of methane emissions in Beijing area using backward trajectory inversion model [J]. Acta Scientiae Circumstantiae, 2002,22(5):586-591.

[9] 李 航,张宏升,蔡旭晖,等.日本福岛核电站泄漏事故污染物扩散的数值模拟与事故释放源项评估[J]. 安全与环境学报, 2013,13(5): 265-270. Li H, Zhang H S, Cai X H, et al. Simulation of the pollutant dispersion and evaluation on the source release accidents in Japan's Fukushima Nuclear Power Plant [J]. Journal of Safety and Environment, 2013, 13(5):265-270.

[10] 张美根.多尺度空气质量模式系统及其验证II.东亚地区对流层臭氧及其前体物模拟[J]. 大气科学, 2005,29(6):84-94.Zhang M G. A multi-scale air quality modeling system and its evaluation II. simulation of tropospheric ozone and its precursors in east asia [J]. Chinese Jo urnal of Atmospheric Sciences, 2005,29(6):84-94.

[11] 唐穗欣.标准遗传算法的原理及算例[J]. 软件导刊, 2007,6(1): 99-101. Tang S X. Principle and example of standard genetic algorithm [J]. Software Guide, 2007,6(1):99-101.

[12] 张丽平,俞欢军,陈德钊,等.粒子群优化算法的分析与改进[J]. 信息与控制, 2004,33(5):513-517. Zhang L P, Yu H J, Chen D Z, et al. AnaIysis and improvement of particle swarm optimization algorithm [J]. Information and Control, 2004,33(5):513-517.

[13] 郑伟博,张纪会.基于Nelder-Mead单纯形法的改进量子行为粒子群算法[J]. 复杂系统与复杂性科学, 2016,13(2):97-104.Zheng W B, Zhang J H. A improved quantum behaved particular swarm optimization algorithm using nelder and mead’s simplex algorithm [J]. Complex Systems and Complexity Science, 2016,13(2):97-104.

[14] 潘 勇,郭晓东.一种基于遗传算法改进的粒子群优化算法[J]. 计算机应用与软件, 2011,28(9):222-224. Pan Y, Guo X D. An improved particle swarm optimisation algorithm based on genetic algorithm [J]. Computer Applications and Software, 2011,28(9):222-224.

[15] 李雅琼.基于粒子群算法的遗传算法优化研究[J]. 兰州文理学院学报(自然科学版), 2017,31(1):55-60. Li Y Q. Research of genetic algorithm based on particular swarm optimization [J]. Journal of Lanzhou University of Arts and Science (NaturalSciences), 2017,31(1):55-60.

[16] 巩永光.粒子群算法与遗传算法的结合研究[J]. 济宁学院学报, 2008,29(6):20-22. Gong Y G. The study of PSO with GA [J]. Journal of Jining University, 2008,29(6):20-22.

[17] 肖宏峰,谭冠政.单纯形搜索在遗传算法中的融合研究[J]. 计算机工程与应用, 2008,44(18):30-33.Xiao H F, Tan G Z. Study on fusing simplex search into genetic algorithm [J]. Computer Engineering and Applications, 2008,44(18):30-33.

[18] 杜修力,崔 冬,侯本伟.基于初始种群改进策略的经验遗传-单纯形算法[J]. 北京工业大学学报, 2014,40(12):1876-1883. Du X L, Cui D, Hou B W. Initial population improvement strategy of empirical genetic-simplex algorithm [J]. Journal of Beijing University of Technology, 2014,40(12):1876-1883.

[19] 何大阔,李延强,王福利.基于单纯形算子的混合遗传算法[J]. 信息与控制, 2001,30(3):276-278.He D K, Li Y Q, Wang F L. Hybrid genetic algorithm based on the operator of pattern search [J]. Information and Control, 2001,30(3):276-278.

[20] 王 芳.粒子群算法的研究[D]. 西南大学, 2006. Wang F. Research on particle swarm algorithm [D]. Southwest University, 2006.

[21] Fan S S, Zahara E. A hybrid simplex search and particle swarm optimization for unconstrained optimization [J]. European Journal of Operational Research, 2007,181(2):527-548.

[22] Vakil Baghmisheh M T, Peimani M, Sadeghi M H, et al. A hybrid particle swarm–Nelder–Mead optimization method for crack detection in cantilever beams [J]. Applied Soft Computing, 2012,12(8):2217-2226.

[23] Ma D, Deng J, Zhang Z. Comparison and improvements of optimization methods for gas emission source identification [J]. Atmospheric Environment, 2013,81:188-198.

[24] Zhang C, Ning J, Lu S, et al. A novel hybrid differential evolution and particle swarm optimization algorithm for unconstrained optimization [J]. Operations Research Letters, 2009,37(2):117-122.

[25] Cantelli A, D'Orta F, Cattini A, et al. Application of genetic algorithm for the simultaneous identification of atmospheric pollution sources [J]. Atmospheric Environment, 2015,115:36-46.

[26] Cervone G, Franzese P. Non-Darwinian evolution for the source detection of atmospheric releases [J]. Atmospheric Environment, 2011, 45(26):4497-4506.

[27] Barad M L. Project prairie grass, a field program in diffusion, [J]. Geophysical Research, 1958,1(59).

[28] Wang Y, Huang L, Huang H, et al. Evaluation of Bayesian source estimation methods with Prairie Grass observations and Gaussian plume model: A comparison of likelihood functions and distance measures [J]. Atmospheric Environment, 2017,152:519-530.

[29] 章 颖,梁漫春,黎 岢,等.基于遗传-模拟退火算法的源项反演方法研究[J]. 核电子学与探测技术, 2014,34(4):451-455. Zhang Y, Liang M C, Li K, et al. Research of source term inversion based on genetic simulated annealing algorithms [J]. Nuclear Electronics & Detection Technology, 2014,34(4):451-455.

Comparative and study on the application of typical hybrid algorithms in source parameter inversions.

SHEN Ze-ya, LANG Jian-lei, CHENG Shui-yuan*, MAO Shu-shuai, CUI Ji-xian

(Key Laboratory of Beijing on Regional Air Pollution Control, Beijing University of Technology, Beijing 100124, China)., 2019,39(8)：3207~3214

Rapid and accurate estimation of source items was the basis for environment emergency disposal on sudden air pollution accidents. In order to search for effective methods for inversing source parameters, we conducted a comparison study on the performances of three hybrid algorithms (e.g., GA-PSO, GA-NM, PSO-NM) for estimating source parameters (strength and location). Three inversion models were developed by combining GA-PSO, GA-NM, PSO-NM with Gaussian dispersion model, respectively. The study was carried out based upon SO2leakage tests selected from 1956 Prairie Grass emission experiment. The impacts of algorithm structure and atmospheric diffusion conditions on source term inversion were analyzed. Results showed that for source strength, the PSO-NM algorithm performed more accurate and robust, the mean error and mean standard deviation were 11.3% and 0.7g/s, respectively, which were much lower than those of GA-NM (i.e., 16.4%, 13.3g/s) and GA-PSO (i.e., 29.0%, 26.6g/s). As for source location, the performance of PSO-NM was more robust, with average standard deviation of 0.29m, which was also much lower than that of GA-NM (3.20m) and GA-PSO (3.03m). Under the unstable and neutral atmospheric diffusion conditions, the accuracy of PSO-NM algorithm for estimating position parameter was the best, with an error of 4.97m; However, GA-NM method had the minimum error (7.69m) under the stable condition. As for computational efficiency, PSO-NM and GA-PSO spent less time in source item inversion, which were more suitable for inversing source parameters for sudden air pollution.

hybrid algorithm；4-D source parameters；Gauss point source plume diffusion model；source parameter inversion；sudden air pollution accidents

X511

A

1000-6923(2019)08-3207-08

沈泽亚(1994-),男,河北唐山人,北京工业大学硕士研究生,主要从事突发大气污染事故源强估算研究.

2019-01-06

国家重点研发计划课题(2017YFC0209901,2017YFC0209905);总理基金项目(DQGG0501,DQGG0509,DQGG0201-02)

* 责任作者, 教授, chengsy@bjut.edu.cn