基于倒塌分析的连续梁桥地震损伤评估方法*

黎雅乐， 宗周红， 黄学漾， 林元铮， 夏 坚

(1.江苏开放大学建筑工程学院 南京，210036) (2.东南大学土木工程学院 南京，210096) (3.福建省建筑科学研究院有限公司 福州，350108) (4.福建省绿色建筑技术重点实验室 福州，350108)

引 言

钢筋混凝土梁桥是我国中小桥的主要桥型，该类桥型在多次地震中都发生过地震损伤，严重时甚至桥梁倒塌。例如：汶川地震中S303线渔子溪2号桥主梁断裂后外倾，之后桥墩倒塌而全桥垮塌；百花大桥大量墩柱被压溃，其中第五联整体倒塌[1-2]。

为保证设计桥梁在地震作用下的安全性，掌握不同地震作用对结构引起的损伤程度，合理评价震后桥梁的适用性，需要开展地震易损性分析。易损性分析指从概率的角度考虑地震动的随机性，建立不同强度地震作用下结构反应超过某种破坏状态的条件概率即易损性曲线[3-4]。为了得到构件的易损性曲线，需要对不同损伤程度进行分级，因此地震损伤评估是易损性分析的基础，而地震损伤评估又依赖于损伤评价指标和损伤状态分级标准，因此损伤指标的选取是易损性分析的核心。

由于桥梁结构的易损性分析可由构件易损性曲线通过概率关系获得，因此结构的易损性问题就成为组成结构的各种构件的易损性问题，针对各构件进行损伤评定。例如，陈立波等[5]以支座剪切应变、桥墩位移延性比、桥台相对位移为损伤指标进行构件易损性曲线计算，将简支梁桥损伤最严重的构件损伤等级定义为桥梁损伤等级进行结构易损性曲线计算。上述易损性研究虽然最终可以给出结构整体的易损性曲线，但无法说明构件损伤导致结构发生倒塌的根本原因，因此结构层次的桥梁地震损伤指标亟待研究。

目前,对于连续梁桥体系中的各组成构件的损伤研究[6-7]已较为充分，但结构倒塌问题仍是研究热点。由于桥梁结构倒塌试验研究的复杂性和安全性问题，目前学者主要从数值仿真角度对桥梁结构开展倒塌研究。亓兴军等[8]利用LS-DYNA软件分析一座四跨30°斜度的装配式连续梁桥在地震作用下的落梁形态。孙鹏等[9]利用ABAQUS软件模拟了一座四跨连续梁桥在地震作用下发生连续倒塌的全过程。左烨等[10]针对3种混凝土连续梁桥进行非线性地震响应分析及倒塌过程的数值仿真。Lee等[11]对2008年日本岩手宫城内陆地震中由于强震和桥下岩体滑移而倒塌的Matsurube大桥进行了倒塌模拟。还有部分学者对连续刚构桥[12]、拱桥[13-14]和斜拉桥[15-16]等其他形式的桥梁结构进行倒塌模拟，这其中关于桥梁结构的倒塌准则和倒塌机理方面的研究尚不多见。

笔者为研究连续梁桥结构层次的损伤评价指标，首先，在振动台试验研究的基础上对连续梁桥进行倒塌分析并通过提出的倒塌准则进行倒塌与否的判定，通过多工况的倒塌分析结果掌握构件损伤到桥梁结构倒塌的基本过程，从而确定影响该桥梁结构倒塌的关键构件；然后，基于关键构件提出两跨连续梁桥地震损伤的整体评价指标D和破坏等级划分标准。

1 倒塌准则

1.1 构件的破坏准则

结构的破坏往往是从构件破坏开始，构件的破坏准则有3种，分别为变形类、刚度类、能量和变形类。其中:变形类的倒塌准则如桥梁规范[17]对于桥墩破坏的限制要求(墩顶位移要小于允许值);刚度类的倒塌准则有增量动力分析(incremental dynamic analysis，简称IDA)准则[18-19];变形和能量类的倒塌准则如Park-Ang损伤指数准则[20]。

1.2 结构的倒塌准则

用构件的破坏准则作为倒塌准则虽然比较安全，但无法描述从损伤至倒塌全过程的内在机理，倒塌的时间、损伤的先后次序等都无法展现。为了倒塌仿真分析能顺利开展，必须先确定倒塌准则。目前，构件层次的倒塌准则存在不足，因此笔者首先需建立一个更有效的倒塌准则。下面从能量平衡角度研究基于结构层次的桥梁倒塌准则。

基于显式积分方法[21]可知，ti时刻结构体系的运动方程为

P(ti)-Ma(ti)-F(ti)+H(ti)=0

(1)

其中：P(t)为ti时刻的外力；M为质量对角矩阵；a(t)为加速度；F(t)为单元应力场的等效节点力矢量；H(t)为沙漏黏性阻尼力。

外力所做功等于结构总能量的增量，对于无损伤结构，结构体系应满足

(2)

其中：ΔEK(ti)，ΔED(ti)，ΔER(ti)，ΔEH(ti)分别为体系ti时刻的动能、阻尼能、应变能、沙漏能增量；ΔE(ti)为体系ti时刻的总能量增量；ΔW(ti)为时间增量Δti-1/2(即ti-1～ti)期间外力所做功。

如果地震作用后结构发生损伤，有限元分析中将删去失效单元相关参数，因此只要存在损伤单元，则有限元分析的剩余结构总能量将不等于结构累积外力功。反之，若式(2)关系不再满足，则必然存在构件损伤。当一定量的关键构件破坏，结构将倒塌。提出一能量比指标ξ(ti)，为ti时刻结构剩余体系总能量E(ti)与0～ti时间内外力功W(ti)之比。假设ti-1时刻结构完好而在Δti-1/2时间间隔内结构发生地震损伤，则ti时刻损伤单元被“杀死”，因此ti时刻的剩余结构由地震作用产生的累计总能量E(ti)和外力累计做功W(ti)分别为

由于E(ti-1)=W(ti-1)，ΔE(ti)=ΔW(ti)，因此

(5)

因为0～ti-1时刻结构完好，所以ξ(ti-1)=1，即ξ(ti-1)>ξ(ti)。假设Δti+1/2(即ti～ti+1)期间不发生新的地震损伤，则

(6)

通过比较式(5),(6)可知，ξ(ti+1)>ξ(ti)。将ξ(ti-1),ξ(t)和ξ(ti+1)相连形成能量比曲线,如见图1所示，发现在ti时刻能量比曲线出现拐点，这是由于ξ(ti-1)>ξ(ti+1)>ξ(ti)的关系形成曲线凹凸发生变化，呈现V字形尖角。由于ti时刻正是结构发生损伤的时刻，因此可以通过能量比曲线的拐点快速找到损伤发生的时间。

图1 结构地震损伤前后能量比曲线变化图Fig.1 Curve variation diagram of energy ratio curve before and after earthquake damage

由图1可见，伴随时间增长，能量比ξ(无量纲)整体呈下降趋势。桥梁结构中的损伤单元继续增加，能量比ξ将不断下降，当损伤程度达到临界状态即为结构倒塌。定义结构倒塌时刻的能量比为ξd，当ξ小于临界值ξd，即认为结构倒塌。判定结构倒塌的分析流程如图2所示。

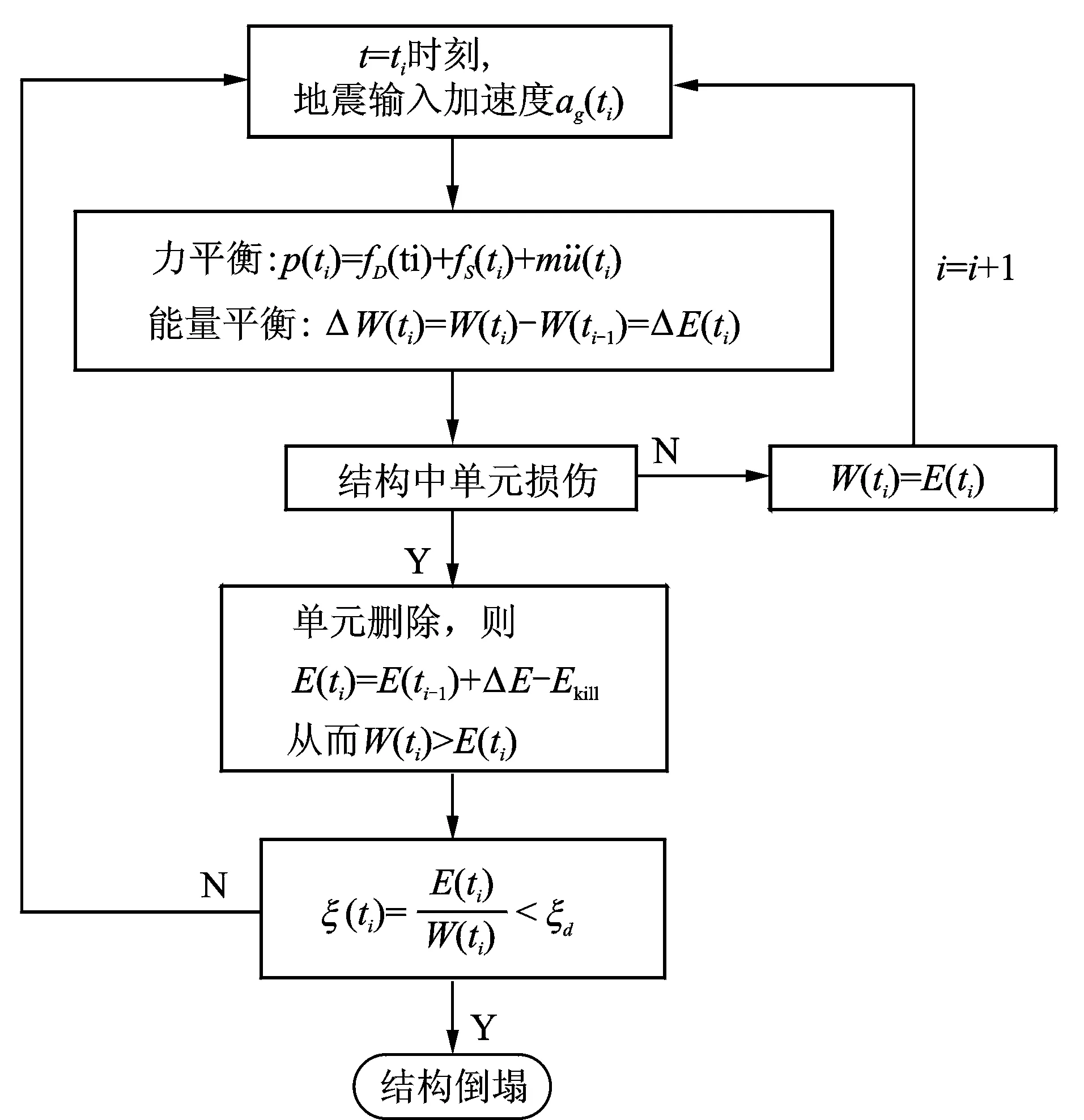
图2 结构倒塌判定流程Fig.2 Judgement process of structural collapse

为了论证该倒塌准则的合理性，以某两跨连续梁模型为研究对象，运用该基于能量平衡的倒塌准则分析整体结构的倒塌时刻和倒塌模式。

2 倒塌破坏分析

2.1 倒塌分析模型桥

图3 振动台试验模型桥Fig.3 Bridge specimen of shaking table test

2.2 有限元分析模型

2.2.1 单元和材料

为得到该模型桥倒塌模式，分析其倒塌机理，基于振动台试验研究成果，采用LS-DYNA软件对该结构的破坏历程进行进一步研究。混凝土为实体单元，立方体抗压强度和单轴抗压强度、单轴抗拉强度分别取32，17.4和1.39 MPa，弹性模量为2.75×104MPa。当混凝土压应变大于等于0.003 3、拉应力大于等于2.24 MPa时材料破坏。桥墩用实体单元模拟，材料特性如表1所示。支座为弹簧单元模拟，通过有限元模型修正确定各支座弹簧刚度，中支座纵、横、竖刚度分别为955，1×103和5×105kN/m，边支座纵、横、竖刚度分别为550，800和2×105kN/m。若弹簧力超过支座最大剪切力则退出工作，改由盖梁和主梁直接作用。采用接触方式仿真，接触的动、静摩擦因数为0.15和0.3。在主梁上附有质量单元模拟配重，建立的有限元分析模型如图4所示。

表1 桥墩钢筋材料参数Tab.1 Material parameters of piers

图4 有限元模型Fig.4 FEA model

2.2.2 有限元模型修正及验证

为确保有限元模型的正确性，以振动台试验[22]实测的自振频率为目标，修正支座弹簧刚度等结构参数，得到修正后的有限元模型修正效果如表2所示。

表2 自振频率对比Tab.2 Vibration mode frequency comparison

2.3 纵向倒塌模式

以纵向倒塌模式为例分析该模型桥的倒塌过程，选取10条具有代表性的地震波进行后续有限元分析，地震波的原始信息如表3所示。根据相似性对各工况的原始波时间进行了压缩，每种地震波工况最终激励至桥梁倒塌。为节约篇幅，仅列举El Centro波和Chi-chi波地震波工况进行分析。

表3 原始地震波信息Tab.3 Original shaking wave details

2.3.1 El Centro波输入工况

在纵向最大峰值加速度(peak ground acceleration，简称PGA)为1.2 g的El Centro波作用下，结构从出现轻微损伤现象到最终倒塌的全过程如图5所示。具体叙述如下：当t为0.81s时，墩底开始出现混凝土开裂；当t为0.84 s时，墩底破坏加剧，部分箍筋裸露；当t为1.05 s时，中支座失效，中墩基本破坏导致主梁失去中墩支承而底部开裂；当t为1.13 s时，T梁梁肋持续开裂；最终在t为1.44s时主梁破坏，桥梁倒塌。在地震输入过程中能量和外力做功的变化曲线如图6所示，两者逐渐产生差异。

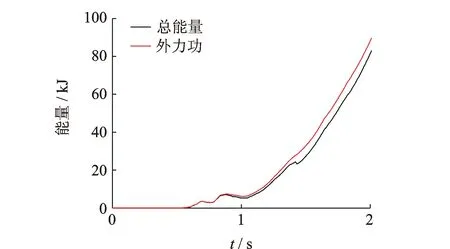
图6 El Centro波工况结构总能量和外力功Fig.6 Total structure energy and external work in El Centro wave case

图7为1.2g的El Centro波工况的能量比变化曲线。可以发现，在图5的各构件损伤破坏时刻能量比都有明显变化，可以有效识别出损伤时间。

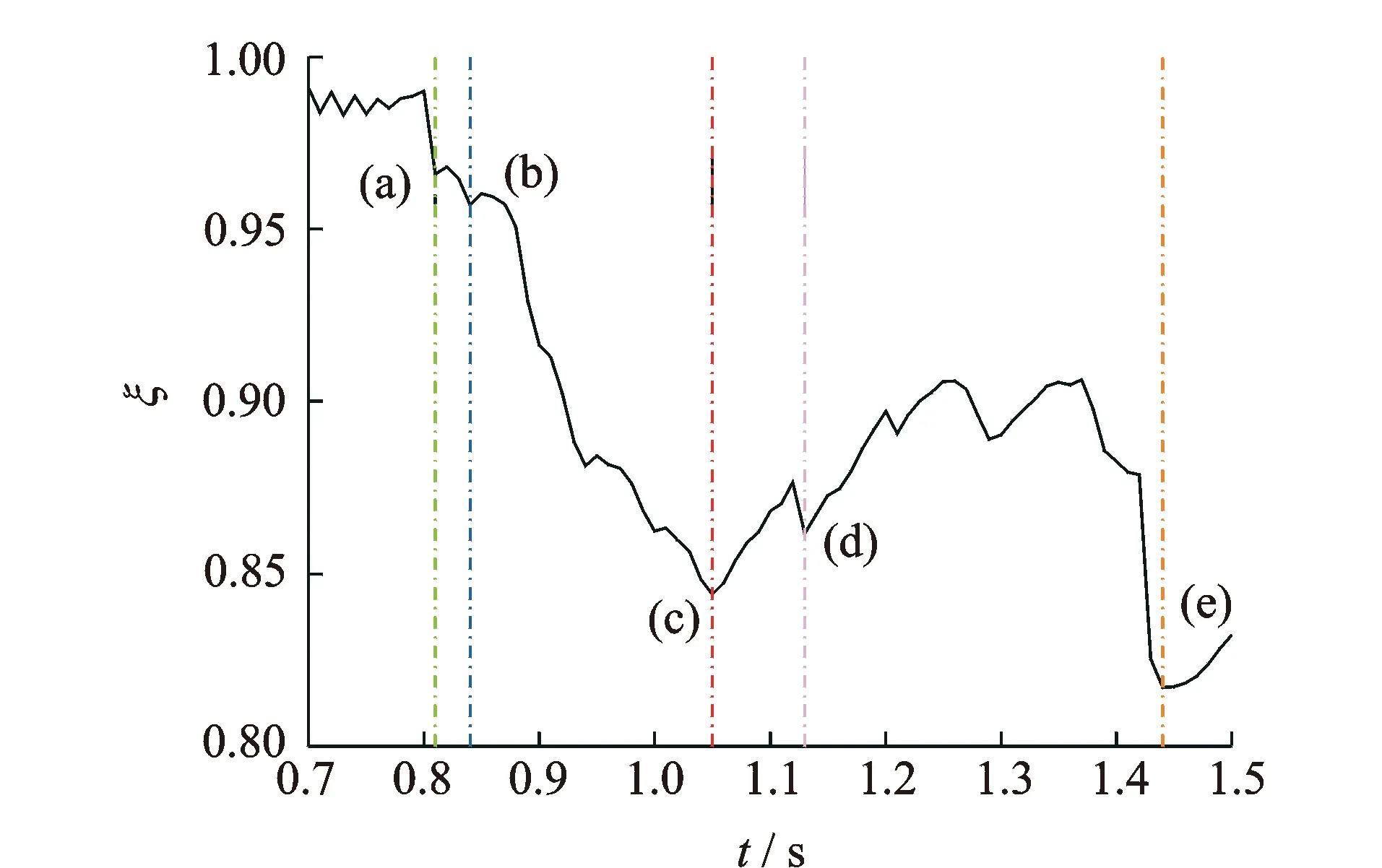
图7 El Centro波工况能量比变化曲线Fig.7 Energy ratio curve in El Centro wave case

2.3.2 Chi-chi波(TCU117)输入工况

图8 Chi-chi波作用下模型桥纵向倒塌模式Fig.8 Longitudinal collapse mode of bridge specimen under Chi-chi wave

如图8所示,当纵向地震动输入为TCU117的Chi-chi地震波时，PGA增加至1.2g结构最终发生倒塌。具体过程如下：当t为8.9 s时，中支座失效，同时引起梁底部分损伤；当t为16.91s时，上部结构几乎脱离桥墩。从图9发现此时已发生40 cm以上的上下部结构间相对位移；当t为17.45 s时，上部主梁一端已离开盖梁向下跌落，可以判定桥梁倒塌。在地震波输入的过程中，同样发现外力所做功逐渐大于剩余结构的总能量，如图10所示。图11的能量比变化曲线也较好地识别出损伤时刻。

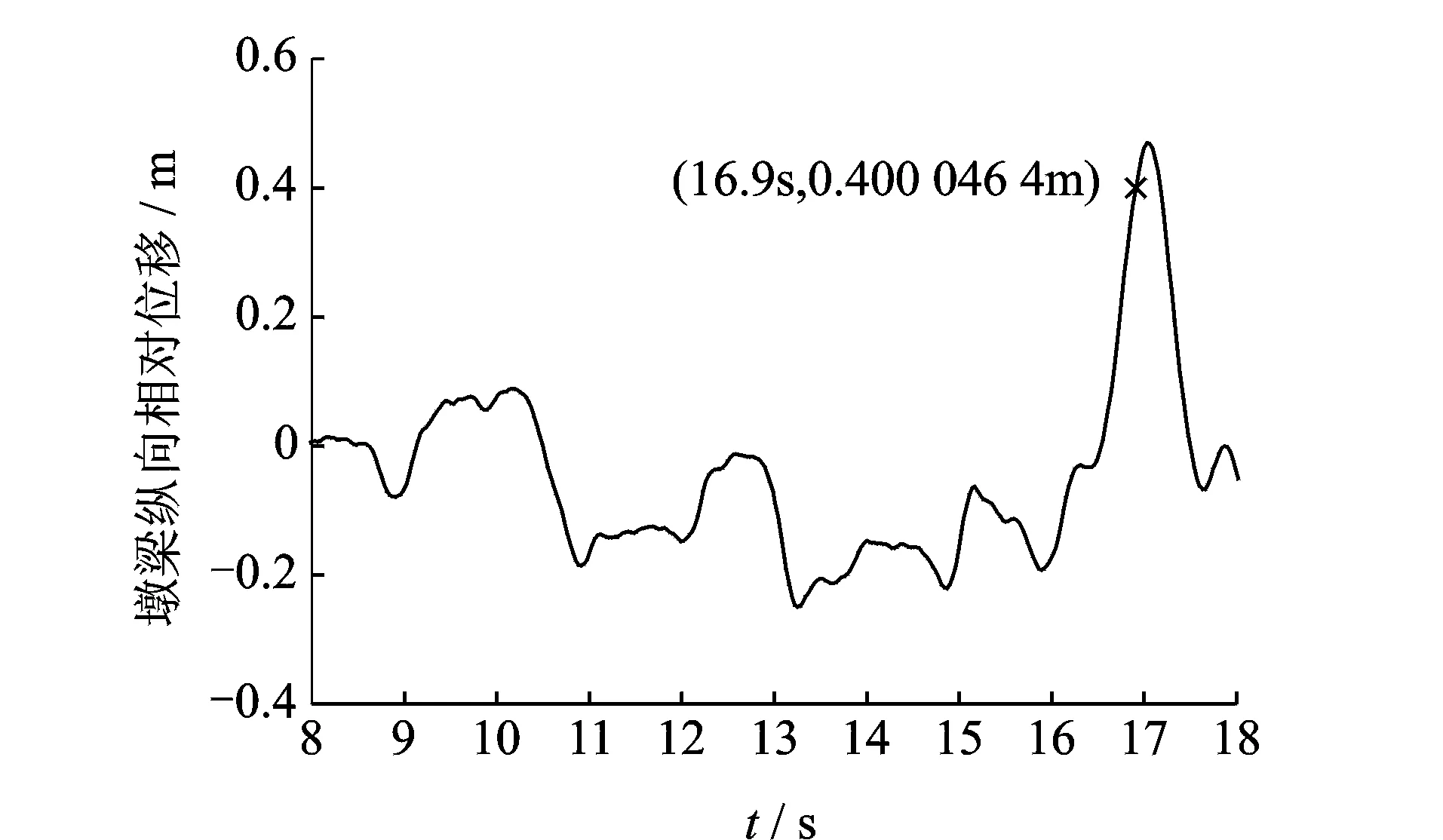
图9 边墩的墩梁纵向相对位移响应时程Fig.9 Relative displacement response of side pier and girder

图10 Chi-chi波工况结构总能量和外力功Fig.10 Total structure energy and external work in Chi-chi wave case

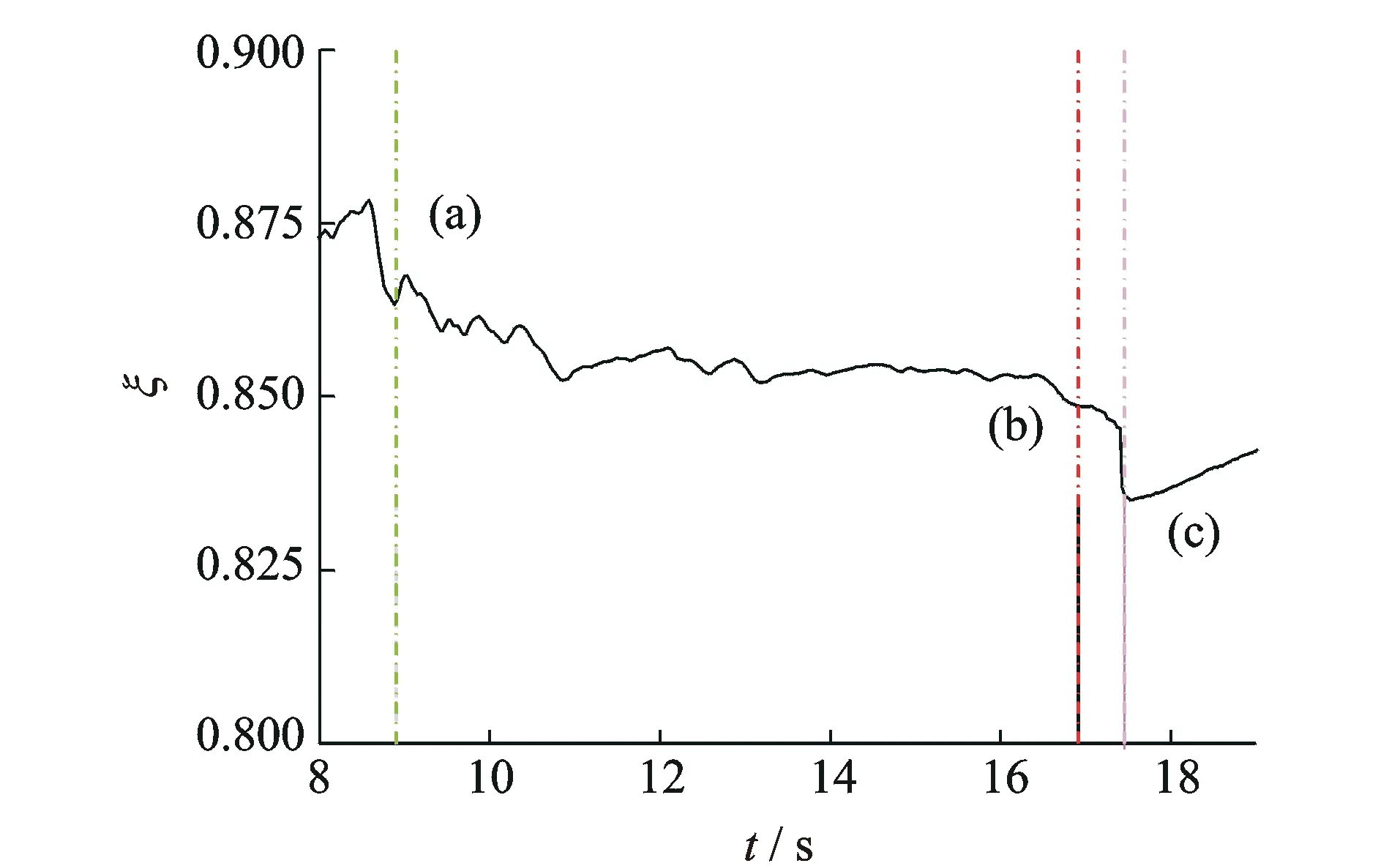
图11 Chi-chi波工况能量比变化曲线Fig.11 Energy ratio curve in Chi-chi wave case

根据图2的设想，当t时刻的剩余结构总能量与外力功之比ξ(t)小于ξd,即可判定整体桥梁结构进入倒塌阶段。由于不同地震动输入工况桥梁结构倒塌瞬时的ξ大小不完全一致(见图12)，但分布在一定区间内且具有统计规律，现假定ξ服从正态分布，取保证率为95%确定ξd的代表值

ζd=μ+1.6σ

(7)

其中：μ为样本均值；σ为样本标准差。

通过分析图12的计算结果，得到均值和标准差，带入式(11)计算得到ξd为90%。

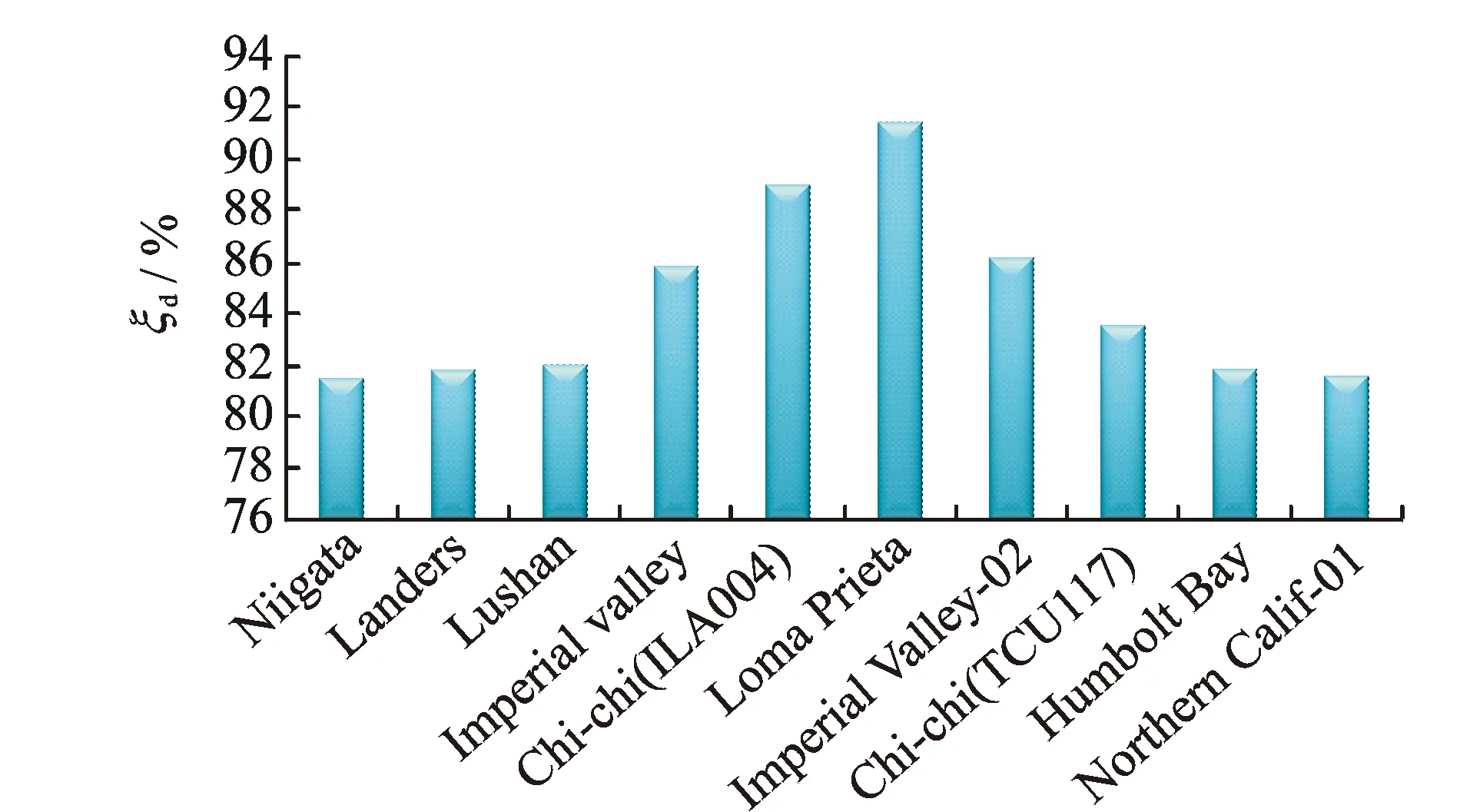
图12 能量比样本图Fig.12 Energy ratio sample diagram

3 桥梁结构地震损伤评估

3.1 损伤指标

倒塌准则判定指标ξ只能评价结构是否倒塌，对于其他程度的损伤不能进行评估。已有的损伤评估指标多为构件层次的指标，笔者提出一种基于结构层次的损伤评价指标D。

研究纵向倒塌模式发现，两跨连续梁模型桥的中墩、固定支座在易损件中最为重要，这两者的失效将引起落梁或结构整体倒塌，因此提出损伤评价指标D为

(8)

3.2 计算示例

为验证损伤评价指标D的正确性，以El Centro波和Chi-chi波纵向地震动工况为例对模型桥地震损伤进行计算分析。有学者对大量墩柱破坏试验结果统计分析发现，规则桥梁破坏时的墩柱漂移率为2.23%[23]，因此笔者将两跨连续梁模型桥的δu1取0.026 8 m。考虑到支座失效时主梁未必落梁，因此δ2取中墩处的墩梁纵向相对位移峰值，δu2为盖梁纵向长度，在本算例中即0.4 m。损伤指标D的计算过程及结果如表4所示。

在El Centro波输入的振动台试验中，0.2g工况仅出现中墩墩底轻微开裂的震害，与表4“基本完好”一致。整体上El Centro波产生的地震损伤其特征为：PGA较小时损伤较小，PGA较大时中支座将剪切破坏，最终中墩墩底完全失效导致上部结构垮塌。

Chi-chi波引起模型桥地震损伤，其特征为：PGA较小时损伤主要由固定墩承担能量输入，中支座剪断后，Chi-chi波中的长周期地震波激发较大的墩梁相对位移产生耗量效果从而分担了下部结构的损伤，因此结构最终倒塌模式是落梁。El Centro波和Chi-chi波工况的破坏特征如表5所示。

3.3 损伤程度分级评定

根据式(8)提出的损伤指标D，分析足够数量的地震动工况计算结果，统计得到本研究的两跨连续梁模型桥的损伤程度与D的分布范围。该类桥型的损伤等级的评定方法如表6所示。

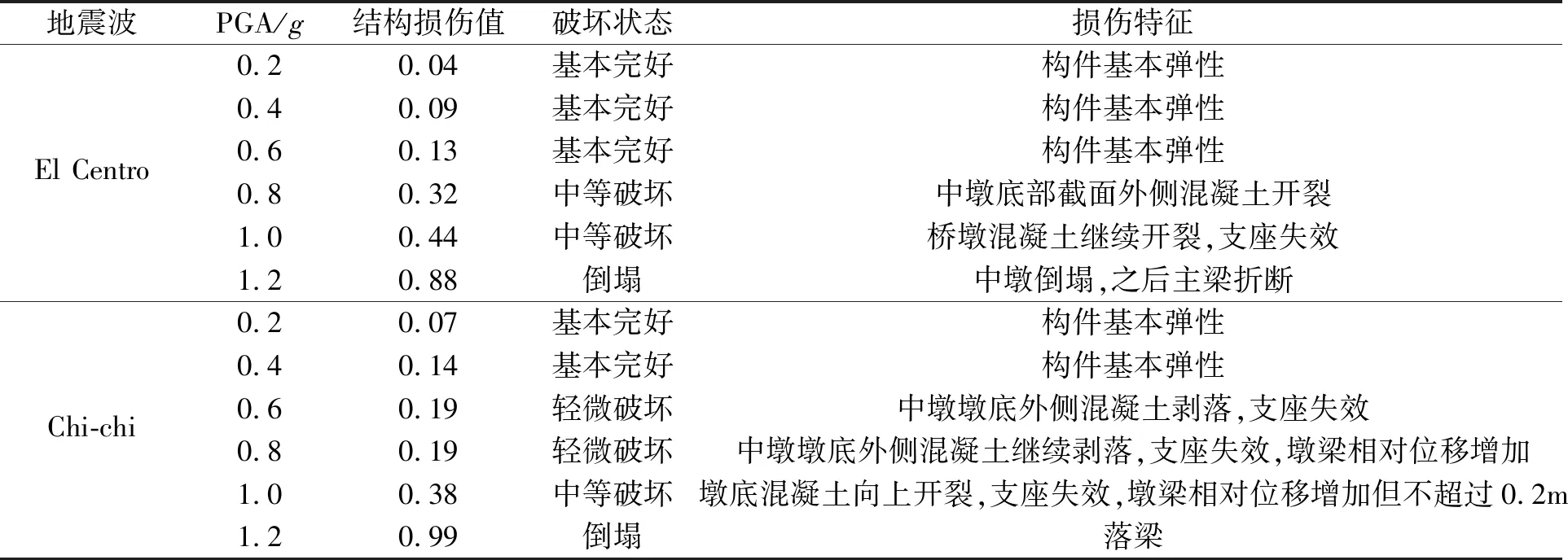
表5 模型桥地震损伤过程Tab.5 Seismic damage process of bridge model

表6 两跨连续梁桥地震损伤分级表Tab.6 Seismic damage classification table of two-span continuous girder bridge

4 结 论

1) 基于能量平衡原理，提出结构层次的桥梁倒塌准则，并建议按95%的保证率确定倒塌准则中的倒塌限值ξd。由该准则提出的能量比ξ不仅可用于判断结构是否倒塌，还能识别结构不同程度的损伤发生的时刻。

2) 通过两跨连续梁模型桥纵向倒塌分析确定中墩墩柱和固定支座为最重要的易损件，说明倒塌分析可以有效识别该模型桥的地震损伤关键受力构件。

3) 提出结构层次的基于关键构件的两跨连续梁桥结构地震损伤指标D，并确立损伤程度与损伤指标之间的关联。算例证明，该损伤评价指标可对不同程度损伤的两跨连续梁模型桥给出合理、有效的评价，该评价方法也可为同类桥型的损伤评价提供参考。