结合模态区间分析和IARR的不确定性损伤识别*

2019-08-28方圣恩

振动、测试与诊断 2019年4期

方圣恩，张宝

(1.福州大学土木工程学院福州，350108) (2.福州大学土木工程防震减灾信息化国家地方联合工程研究中心福州，350108)

引言

结构健康监测与安全状态评估的核心内容之一是基于静动力响应测试数据来识别结构可能存在的损伤[1]，但工程结构中总是存在不确定性因素，导致确定性损伤识别方法实用性不强[2]。为此，在概率统计框架下考虑上述不确定性因素，量化参数的不确定性[3]，建立概率损伤识别过程，是近几年的研究热点。具体来说，可以采用随机有限元[4]，通过对模型参数摄动式的随机模拟来获取参数的概率统计特征；也可以基于统计模式识别[5]，基于响应时程数据的统计特征构建表征结构状态的统计模式向量，通过比较不同状态下的模式向量在特征空间的距离来判断损伤；或者利用贝叶斯公式建立贝叶斯推断过程[6]，基于结构参数先验分布和当前实测信息不断更新参数后验概率分布，建立概率损伤指标来判断结构是否发生损伤。可以说，概率统计理论在损伤识别实用化进程中非常重要。对几何尺寸大、构件数目和种类繁多、材料性能复杂的土木工程结构而言，大样本量的实测数据在测试时间和成本上难以接受，且工程上更关心的是结构参数和响应的上下界，因此经典区间分析(classic interval analysis,简称CIA)的优势就得到了利用[7-8]。

可以由包含不确定性的实测响应数据得到结构健康特征量，并以区间量或区间向量的形式来表示[8]。将结构不确定性量用有界区间数表示，通过区间修正方法得到完好与损伤结构的区间模型，根据损伤存在可能性指标判断结构各单元损伤情况[9]，其单元刚度参数上下界可以由一阶泰勒级数展开式来表示[10]。区间建模技术可以有效提取结构损伤特征，与自适应神经模糊推断系统相结合，可实现对结构损伤的快速诊断[11]。但是，传统的区间算法容易发生区间扩张，使估计的参数区间范围大于真实区间，造成识别结果精度不足。为此，文献[12]提出了模态区间分析(modal interval analysis,简称MIA)方法，通过定义逻辑谓词和语义函数进行区间分析，用不规范区间考虑了变量之间的相关性，从而得出参数的精确区间包络线，可以与响应面法相结合用于区间参数的识别[13]。

约束满足问题(constraint satisfaction problem,简称CSP)[14-15]用于损伤识别时需要测量节点或截面的转角位移，虽然通过解析冗余度(analytical redundancy reduction,简称ARR)可以剔除转角未知量，但无法实现损伤定位。笔者提出的改进解析冗余度方法可以仅用相对容易测量的位移或振型来判断结构是否发生损伤并定位，分析过程无需构建结构数值模型并进行模型修正，属于一种无模型的损伤识别方法。为了进一步考虑损伤识别中的不确定性，笔者将MIA和ARR相结合，提出模态区间约束条件和模态区间中心预处理方法，通过对比结构损伤前后参数区间约束条件变化情况，实现损伤定位。最后，用一根试验钢梁验证了所提出方法的可行性。

1 经典和模态区间分析

1.1 经典区间算法

区间宽度W和区间中心O定义为

(1a)

(1b)

区间四则运算与传统数学运算法有显著区别[7]，函数f(x)的区间运算过程通常都会发生区间扩张现象，即估计的f(x)区间大于真实区间。例如：一元函数f1(x)=x(10-x)和f2(x)=10x-x2，二者在传统数学上完全一样，但若x为区间数xI=[4,6]，则由区间运算可得f1(xI)=[16,36]，f2(xI)=[4,44]，而准确的区间解为[24,25]，为前述计算的两个区间所包含，即发生了区间扩张现象，对f2(xI)来说更严重。原因有两方面：a.函数区间分析过程中，表达式中同一变量xI的两次出现被看作是两个完全独立的变量，从而产生了区间扩张；b.不同的函数表达式导致不同的扩张结果，这是由于区间的弱分配律和区间包含特性所致，且扩张程度会随着区间变量和运算次数增多而变大。

1.2 模态区间分析

MIA[12]可以看作是CIA和模态逻辑理论的有机结合，利用模态逻辑谓词对区间进行语义学解释，从而得到符合模态逻辑语义解释的区间分析方法。若I(R):={[a,b]|a,b∈R,a≤b}，引入存在量词E和全局量词U，则模态区间的规范化表示为

(2)

其中：([a,b],E)为“规范区间”或“存在区间”；([a,b],U)为“不规范区间”或“全局区间”。

可见，通过引入逻辑谓词，使模态区间也具有绝对值相同、符号相反的区间(像实数那样)，这是CIA所不具备的。具体应用上，MIA通过对偶算子Dual实现规范到不规范区间的变换，即Dual([a,b])=[b,a]，由此延伸出MIA中的两个理论。

f*(X′)=C(X′D)=f**(X′)

(3)

其中：f*和f**为语义函数。

2) 部分强制最优理论：若C(X)只对X′中的部分X完全单调，则对于完全单调的部分，若X′D中的任一变量与X′的单调性不一致，则将该单一变量在函数中作对偶。对于不完全单调的部分，对X′不规范区间向量中除一个变量外的其余所有变量作对偶，将X′D转化为X′DT*，并对所计算结果取并集，由此计算出的结果将是近似区间解

f*(X′)⊆

(4)

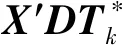
可见，MIA与CIA的运算规则类似，但MIA的四则运算法则中存在不规范区间，并在分析过程用不规范区间考虑了变量之间的相关性，有效避免了区间扩张，这也是MIA和CIA最大不同之处。仍以函数f2(x)=10x-x2在变量x=[4,6]时为例，CIA的计算结果为[4,44]，而MIA应用强制最优理论的计算结果为精确解[24,25]，由此可见后者有效解决了区间扩张问题。限于篇幅，此处不再详细介绍MIA，具体理论可参见文献[12]。

2 不确定性损伤识别

2.1 约束满足问题及改进解析冗余度

CSP是人工智能领域的一个重要基本问题[16]，由一个变量集合和一个约束集合组成。经典CSP通过一个三元组[X,D,C]定义

(5)

其中：X为CSP中变量集合；D为X中各变量的取值域集合；C为约束条件集合，可以定义为函数方程及不等式等。

若找到赋值X1=x1,X2=x2,…,Xn=xn，使C中所有约束条件都满足，则集合{x1,x2,…,xn}就是该CSP的一个解。损伤识别问题中，当一个或多个Ci(x)无法满足时，就称为发生了不一致，表示为

∀x∈X{(C1(x))∨…∨(Cm(x))}

(6)

结构静力分析时，可将结构刚度方程写成矩阵的形式

其中：Δt和Δθ分别为节点平动和转动位移；Ktt和Kθθ对应平动和转动的部分刚度矩阵；交叉项为Ktθ=Kθt；Pt和Pθ为作用在结构上的集中荷载和力矩。

结构参数变量均包含在刚度(子)矩阵K中，即认为损伤引起的参数变化反映为刚度的降低。式(7)分解为方程组时就形成了CSP，每个方程代表1个约束条件。为消除难以实测的Δθ，ARR法以包含了Δt，Δθ的部分约束方程为基础，假定Δt为已知量来表示Δθ，形成以Δθ为因变量的转换方程，再代入剩余的CSP方程组中，最终得到只含Δt的方程组[15]。由于转换后方程组仍包含了与损伤单元相关的方程，使所构造的CSP只能用于判断整体结构是否发生损伤，无法进行损伤定位。

为此，笔者提出了IARR方法，预先假定可能损伤单元，通过消除与Δθ相关的方程组，剔除了与假定损伤单元相关的方程，同时补充了与损伤单元无关的方程来形成新的CSP求解方程组

(8a)

(8b)

将式8(b)求解结果代入式8(a)中，得到不包含Δθ方程组子集KtΔt=Pt，以此作为约束关系集合，将结构损伤识别问题就变成一个只包含可测量Δt的CSP，展开式为

(9)

表1 结构约束条件满足情况

Tab.1 Satisfaction of structural constraints conditions

结构状态约束条Cx()¨Cx()无损TCx()=0)T(¨Cx()=0)假定单元发生损伤TCx()=0)F(¨Cx()≠0)其余单元发生损伤FCx()≠0)T(¨Cx()=0)

2.2 结合MIA的不确定性损伤识别

实际工程结构参数x往往带有不确定性，满足某一概率分布或处于一定取值范围，后者可用区间数xI表示，此时相应的CSP约束条件方程也扩展成区间形式，通过MIA计算判断约束条件是否满足，即约束区间值是否包含0值。和表1类似，结构区间约束条件如表2所示。

表2 结构区间约束条件满足情况

Tab.2Satisfaction of structural interval constraints conditions

结构状态约束条CxI()¨CxI()无损T(0CxI())T(0∈¨CxI())假定单元发生损伤T(0CxI())F(0∉¨CxI())其余单元发生损伤F(0CxI())T(0∈¨CxI())

除了结构参数不确定性，实际测试中还存在仪器系统误差、测量噪声、环境温湿度变化及人为因素等不确定性因素，部分因素难以量化。分析过程若考虑过多的不确定性组合，会导致求解的结构响应区间范围变得很大，使结构发生较大程度损伤时才能被识别，无法体现“早发现、早处理”的目标。分析中未考虑的不确定性因素也会使响应区间发生“偏差”，表现为结构无损伤时响应区间不包含零值。为了在简化问题的同时避免上述“偏差”，笔者采用区间中心O(式(1))预处理结构在无损状态下的响应区间

(10)

其中：上标u表示无损(undamaged)。

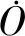
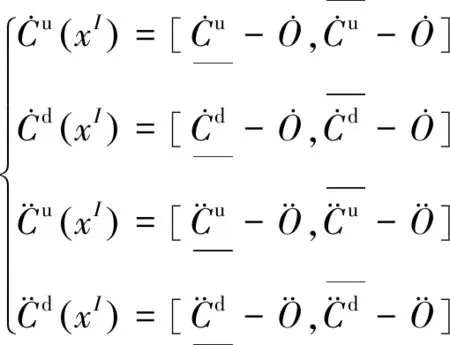
(11)

具体的不确定性损伤识别流程如图1所示。

图1 不确定性损伤识别流程Fig.1 Flow chart of uncertainty-based damage identification

3 钢梁试验算例

实际工程中监测处于交通生命线上桥梁结构的健康状态是十分必要的，而主梁又是桥梁主体结构中最关键和最常受损的构件。为结合工程实际并验证所提出的不确定性损伤识别方法，笔者实测了一根薄壁矩形截面钢梁，几何尺寸如图2所示。钢材实测屈服强度为343 MPa，抗拉极限为450 MPa，弹性模量为202 GPa。试验通过在钢梁截面上切口来模拟损伤，采用千斤顶静力加载方式得到钢梁的挠度，作为目标响应。

3.1 钢梁计算模型和约束条件

静载试验时钢梁两端边界条件为简支，在距左端支座1/3梁长处施加竖直向下的集中荷载P。试验前先建立钢梁的计算模型，将梁划分为6个识别区域(梁段)，每个梁段对应的约束条件如图3所示。梁段划分长度根据识别精度要求来确定，刚开始可以先粗划分，确定可能发生损伤的梁段后，再针对此梁段进行细化分，以准确定位损伤。弹性模量E、竖向挠度d及外荷载P为随机变量：E的区间范围根据试验结果设为[190,210] GPa；d的不确定性根据千分表的精度设为±0.001 mm；P的不确定性力根据千斤顶的力传感器精度设为±100 N。

限于篇幅，算例中假定梁段4发生损伤并建立该梁段的CSP，相应的求解方程组和约束条件如表3所示。其中，支座处竖向位移为0，故相应的约束条件C1，C13和竖向挠度变量d1，d13恒为0，不在图表中列出。得到的约束条件方程为

其中：E，d及P为区间变量(为简化表示，不作上标I)。

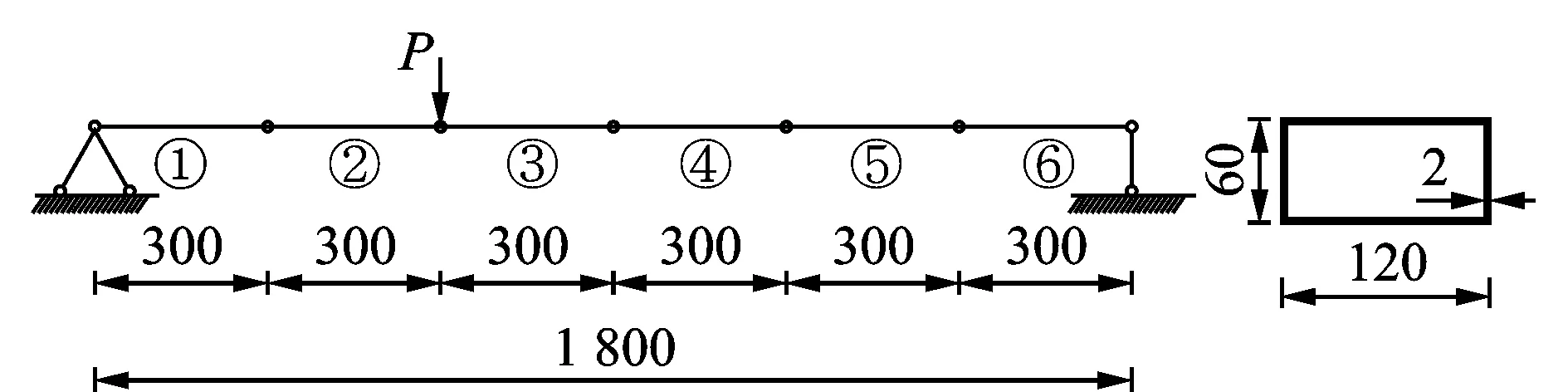
图2 试验钢梁示意图(单位：mm)Fig.2 Schematic diagram of experimental steel beam (unit: mm)

图3 钢梁梁段划分及约束条件Fig.3 Segment division and corresponding constraints of steel beam

项目内容假定损伤梁段④转角变量θ2,θ4,θ6,θ8,θ10,θ12,θ14竖向位移变量d3,d5,d7,d9,d11用于求解的方程组C2,C4,C5,C6,C11,C12,C14与损伤单元无关的约束条件方程C3与损伤单元有关的约束条件方程C7,C8,C9,C10

3.2 试验过程

试验加载系统由反力架、支座、油压千斤顶及力传感器等组成，如图4所示。按图2将梁划分为6段，除支座外的分段梁截面下共布置5个千分表。试验中钢梁在第4梁段中间截面转角处采用切割方式模拟单损伤(图4右上角)，分为3种损伤程度逐步增加的工况，切割宽度均为0.8 cm，长度分别为1，2和3 cm。值得注意的是，切割宽度仅为该梁段长度(300 mm)的2.7%，3种切口对箱梁截面惯性矩降低的程度分别为1.4%，2.1%和2.7%。可见，对钢梁来说是很小的损伤，目的是为了增加识别的难度。

图4 试验钢梁静力加载及损伤模拟Fig.4 Static loading and damage simulation of experimental steel beam

试验前首先进行预加载，以检查测量系统的稳定性并压实梁与支座、加载系统间的缝隙。正式加载时荷载步为1 kN，逐步加载至4 kN后维持该荷载，并记录钢梁在无损状态下的挠度数据。然后，在预定位置切割，每个工况切割完毕后，记录钢梁在受损状态下的挠度。

3.3 损伤识别结果

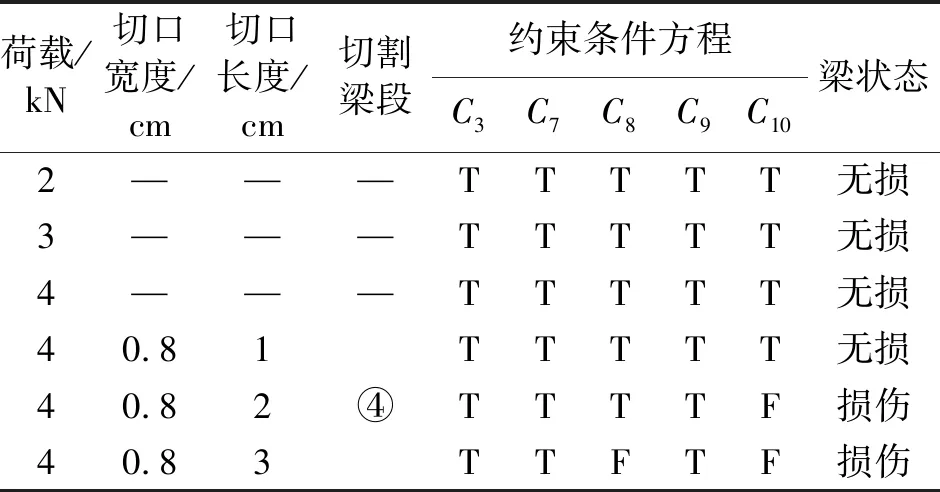
结合梁计算模型和实测挠度数据进行了不确定性损伤识别过程，如表4所示。表中不仅列出与损伤梁段4相关的4个约束条件C7～C10，也将无损梁段1，2的约束条件C3进行对比。约束条件值为T说明无损伤，为F时说明发生损伤。由表4可见：a.P<4 kN的无损状态下，C3,C7～C10均为T，表示梁未发生损伤，与实际情况相符;b.P=4 kN、切割长度为1 cm时，C3,C7～C10均为T，未能识别出该工况的损伤，可能是由于损伤程度太小所致;c.P=4 kN、切割长度为2 cm时，C10为F，说明梁存在损伤，损伤位置为第4或第5梁段(因为C10为这两段共同的约束条件)；d.P=4 kN、切割长度增加到3 cm时，C8和C10均变为F，说明梁的损伤在增大，且此时可以确认损伤位置处于第4段。

表4 静力损伤试验约束条件满足情况

Tab.4 Scenarios of damages in static test