基于磁梯度张量的磁目标模式识别方法

郑建拥,范红波,张 琪,李志宁

(1.陆军工程大学石家庄校区,河北 石家庄 050003；(2.中国人民解放军94019部队,新疆 和田 848000 )

0 前言

利用磁异常信号,对地下或水下物体进行探测,一直是备受学者关注的领域。但大量的地磁研究主要侧重于大型地质体,或水下大型目标如潜艇的探测，而对地下(水下)诸如铁管道、未爆弹药等小型铁质体,始终缺乏成熟的研究。而磁梯度张量受到广泛关注,为探测小型目标的形状、大小、姿态等信息提供了新的工具[1]。

目前国内外针对磁性目标的识别方法开展广泛研究。2014年孙刃较系统地分析总结了磁异常正反演识别目标的方法,并将之用于水下沉船、管线、未爆军火等目标的探测[2]。2015年吴国超则提出利用张量矩阵特征值和6个矩阵元素对大型地质体进行边界识别,分辨率较高,试验得出了很好的效果[3]。地质大学的徐熠提出了基于磁梯度张量的异常反演的算法与算例,将张量矩阵引入磁异常数据反演[4]。2016年李金朋等也提出了在地下小目标的反演、3D成像等方面研究成果[5]。2016年尹刚提出利用张量不变量和矩阵特征值来定位磁目标[6]。上述方法主要研究磁性目标的二维边界识别、三维姿态反演、磁性目标定位方法,是局部磁异常识别方法。需要繁杂的理论推导、公式演算、算法设计,以及对磁测数据进行大量的解析运算,且脱离不开磁测数据正演、反演的范围,受测量数据精度限制大,不能详细清晰地表现磁测目标。相较于以上的磁目标识别方法,早在1994年,Luthi.S.M就提出了利用聚类分析处理地球物理图像信号[7]。1997年I.Rosati和E.Cardarelli提出了提取地球物理信号图像的纹理特征进行模式识别的方法[8]。2008年Brown.M.和Poulton.M.曾利用神经网络定位地下目标[9]。2010年Calderón-MacíasC,Sen.M.K,Stoffa.P.L.利用人工神经网络对地球物理信号进行处理[10]。2010年Bernd和Ehret提出了利用支持向量机对地探雷达信号进行模式识别[11]。这些方法证明了人工智能和机器学习适用于地球物理领域,已经有了一定的工程应用的基础,并且研究潜力巨大。而中国地质大学谢永茂则提出建立模板库,利用模板匹配的方式来识别剖面局部异常[12]，但是他所提出的模板匹配的方法缺乏实际工程应用。对待识别的目标缺乏足够丰富的样本信息,且一维的剖面分析对目标特征信息遗漏比较大,工程应用并不理想。本文针对以上的问题,提出了基于磁梯度张量的地下磁目标模式识别方法。

1 磁梯度张量与模式识别

1.1 张量矩阵

地磁总场包括地磁场和异常场。其中地磁场的空间变化率很小,在小范围内可以认为它是一个定值,所以可以认为磁梯度张量就是磁异常矢量三个方向上的变化率。且梯度张量元素受地磁场倾向、偏角影响小,经过反演能够更精确地描述场源体的磁化方向和几何形态[13]。

磁场是具有方向的矢量场,其三分量的梯度矩阵构造表达式为:

(1)

式(1)中,U为磁标势,矩阵中的9个元素即为磁场矢量B在空间相互正交的三个方向上的分量的变化率。磁法勘探中地磁场及铁磁物质产生的异常场可看作无源的静磁场,因此,磁感应强度的散度和旋度为0[14],如式(2)：

(2)

又因矩阵对称,可得9个元素中只有5个相互独立。

本文选择了磁总场强度(Total Magnetic Intensity,TMI)、张量矩阵特征值的最大值(Tensor Matrix Maximum Eigenvalue,ME)、两个矩阵不变量(I1、I2)及5个张量矩阵独立元素作为特征量。并构造为支持向量机分类的特征向量,作为支持向量机的训练和测试数据。其中,TMI和I1、I2的公式如下:

(3)

(4)

式(4)中，定义λ1,λ2,λ3为张量矩阵G的特征值[13]。

1.2 模式识别

模式识别,就是通过计算机用数学技术方法来研究模式的自动处理和判读。为有效地识别小型地下磁目标,本文采用了支持向量机。支持向量机需对分类对象进行特征提取,目的是最大限度地从原始数据中提取特征以供算法和模型使用。每一个特征都与分类对象本身具有相关性,且能表现出对不同类型的离散[15-18]。

作为一种模式识别方法,支持向量机(Support Vector Machine,SVM)可用于模式分类和非线性回归,具有结构风险最小化优势,拥有很好的泛化性能。

(5)

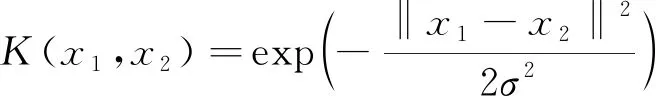
加入松弛因子ξ(i)后,支持向量机优化的目标函数和约束条件为:

(6)

式(6)中,w即将目标分类的超平面的法向量。支持向量机受到影响的因素却十分多,如上式中的惩罚因子c以及核函数参数g,g代指式(5)中核函数方程中的σ,对于小型样本分类精准度的影响最大。因此,在应用SVM做分类预测时惩罚参数c和核函数参数g的选取便成了关键。

而本文采用的QPSO是从量子力学的角度提出了一种新的PSO算法模型,因其认为粒子具有量子行为,故称其为量子粒子群算法。具体为,在有m个粒子进行寻优的j维搜索空间中,第i个粒子的位置为xi=(xi1,xi2,…,xij);第i个粒子的最优位置为Pi=(Pi1,Pi2,…,Pij);整个粒子群所搜索到的最优解Pg=(Pg1,Pg2,…,Pgj)。其中,粒子即参数c和g,Pi为每代局部最优,Pg为全局最优。通过200代的迭代,选取全局最优的c和g[16-17]。

粒子的位置方程为:

(7)

式(7)中,mbest是粒子群pbest的中间位置；M为粒子的数目;j为粒子的维数;Pi为粒子的最佳位置；Pij为粒子本身所能找到的最优解pbest；Pgj为整个种群目前找到的最优解gbest；xi(t)是粒子的想关位置信息；β为QPSO的收缩系数；u、r1和r2是[0,1]之间的随机数。在迭代过程中,±是由[0,1]之间的随机数u的大小决定的,大于0.5时取负；其余情况取正。最后得到进化n代之后的Pij,即为最优参数c和g。基于粒子群算法优化后的c和g,建立最优化QPSO-SVM分类模型。

2 信号处理与识别过程

本方法首先通过磁通门阵列测得地下水平不同形状目标的磁异常数据,但磁异常数据受背景场影响较大,包含大量噪声,而又受到斜磁化的影响,信号质量并不好。并且因为实验操作比较困难,实际采集支持向量机所需要的大量的训练样本并不现实。因此,创新地提出利用化极技术对信号预处理,并利用延拓技术扩展磁测信号样本库,为下一步的模式识别提供更准确、更丰富的特征信息。

2.1 化极原理

化极指把斜磁化的异常化为垂直磁化(化到地磁极),是消除由于磁化场的倾角和偏角引起的磁异常的不对称性的一种滤波技术。在垂直磁化的条件下,磁异常的形态等比较简单,便于分析和解释。

磁异常化极计算在空间域为复杂的褶积计算,而在频率域为简单的乘积运算,所以在频率域中的转换计算只需要乘上相应的的转换因子,然后反变换到空间域就可得到转换后的空问域结果。公式表述为[19-20]:

Q·H=AQ·eiφQ·AH·eiφH=
AQ·AH·ei(φQ+iφH)

(8)

式(8)中，Q为磁场频谱,AQ为磁场振幅谱函数,φQ为磁场相位谱函数,H为化极因子频谱,AH为化极因子振幅谱函数,φH为化极因子相位相位谱函数。频率域中的化极因子H(u,v)表达式为:

(9)

将式(9)中的qk分解为振幅谱和相位谱可得:

qk=Ak·eiφk

(10)

式(10)中,

图1为实际测量的长1 m,口径20 cm埋深1 m处的铁圆柱体的磁异常信号平面。实验使用边长2 m的正方形实验台(详见图4),每隔0.1 m设置一个测量点,利用磁通门所测的20×20个测量点从而组成磁异常信号平面。为了直观地证明化极对磁异常信号处理的作用,图1列出了频率域化极前后,磁异常总场强度TMI的数据平面的等高线云图。

由于实验地点的磁倾角大约为55°,明显可见化极之前,数据斜磁化现象严重,磁阳极和阴极落差明显,掩盖了一部分形状特征信息,不利于目标的识别。而在化极之后,虽然噪声仍然存在,但目标的形态基本显现出来,可以更清晰地观测出磁目标的形状信息。而噪声会在下一步继续处理。

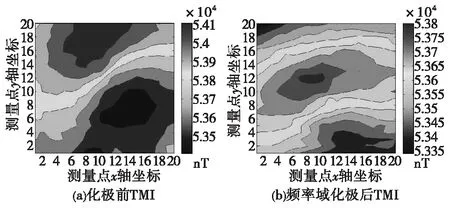
图1 化极处理前后的TMI数据平面等值线图Fig.1 Data plane contour plot before and after reducing to the pole

2.2 延拓原理

磁场延拓就是将实际测量所得数据转换到不同假想高度上的过程。通常,我们所测的磁场数据是在地面或者高于地面的某一高度中获得的。而本文使用的模式识别方法的准确性依赖于大量的数据样本。利用延拓方法,扩大已有的训练样本,发掘数据潜在的信息,更准确地分析测量对象特征,也是提高识别正确率的重要方法。

延拓的基本原理在于根据已知的边界条件(已知测量面的数据)求解拉普拉斯方程,得到高于已知平面ΓA上任意高度的数据。磁场向上延拓原理描述如图2,磁性目标M位于实际测量面某一位置,需要将数据延拓至实测面以上ΓB处[21]。

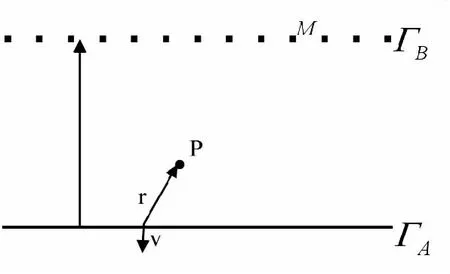
图2 延拓原理图Fig.2 Schematic diagram of continuation

已知,标量磁势满足拉普拉斯方程:

2U=0

(11)

式(11)中,U代表标量磁势。测量面上的磁测数据已知,边界条件已给定,也就能够建立已知平面ΓA与其上任意高度平面ΓB的磁场间的关系,即可求解式(11),从而解决了向上延拓的问题。

但在实际的磁测勘探工作中,如果测量面在地面或者地面附近空间,当观测面为平面时,可以得到消除法向导数后的平面上任意点M的磁势表达式如式(12),求出观测面上半空间中的磁异常,实现解析向上延拓。

(12)

实际测量中,一般采用式(12)延拓。

为了直观地显示延拓的处理作用,图3列出了延拓前后铁圆柱体的磁异常ME数据(化极后)信号平面。实验的条件设置同图1，使用同一张原始数据。

图3(a)为原始信号,图3(b)为向上延拓1 m后所得的数据面平面。可以看出,延拓后数据被调和,压制了高频噪声,即削弱了局部异常干扰,突出区域性异常特征。曲线边界更光滑,没有了畸变点。延拓数个数据平面之后,样本数据库所含目标的信息更丰富。

经过化极和延拓处理之后,由图1和图3可见信号的质量和数量得到了很大的改善。此后,根据式(1)-式(4),计算出9个特征量平面矩阵。计算出所有矩阵的最大特征值,并将其构造为特征向量,以此建立支持向量机。最后用建立的支持向量机对测量数据进行模式识别,来识别目标形状。

图3 原始信号与延拓后数据平面等值线图Fig.3 Data plane contour map of the original signal and after continuation

3 实验验证

为验证本文所提出的形状识别方法的可行性,设计实验采用口径分别为20 cm和10 cm,长度分别为1 m和0.8 m的两个铁圆柱,和一个铁圆板作为识别对象,并在实验开始前先测量地磁背景场,作为第四种类型(即为无目标),分类标签分别设置为1，2，3，4。在支持向量机中,分类结果通过输出整数字来表示,每个数字代表一种分类结果。设置水平埋深为2 m。搭建边长2 m的水平正方形实验测量面,每隔0.1 m设置一测量点,采用4个磁通门传感器构建了平面十字形磁梯度张量系统,测量正方形实验面中包含20×20个测量点的三种样品的磁异常数据平面,数据结构为一个20×20的矩阵。

提取出所有测量点的9个特征量,之后分别计算出每种分类样本、每个特征量的磁异常数据平面矩阵的特征值(每9个特征量矩阵的特征值的输入对应输出一个1～4的数字)。最后将4组,每组是一种类别,包含20个列向量的数据,每个列向量都是10维,对应9个特征量和其所代表的输出结果的整数。构造成支持向量机的分类特征向量,数据结构为(9+1)×80的矩阵,并以3∶2的比例随机分成训练样本和测试样本(图5中32即为测试样本数),建立了支持向量机。

作为对照实验,对所测得的数据进行化极处理后,向上每隔0.2 m一次延拓10次,数据结构为(9+1)×1 600的矩阵,并以3∶2的比例随机分成训练样本和测试样本(图6中640即为测试样本数),建立了磁异常数据库。实验装置设计如图4所示

图4 实验台设计Fig.4 Bench design

采用QPSO-SVM对两个数据库的样本进行分类。图5和图6分别为用化极和延拓方法处理磁异常数据前后,模式识别结果的对比。输出的数字代表结果的类型标签。用测试样本原始标签(预测分类)和支持向量机输出的标签(实际分类)对比,可以得出正确率。

图5 化极、延拓前模式识别结果Fig.5 Pattern recognition results after reducing to the pole and continuation

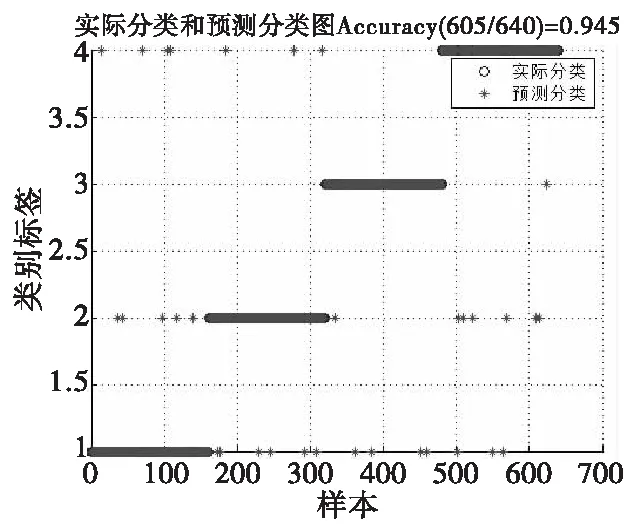
图6 化极、延拓后模式识别结果Fig.6 Pattern recognition results after reducing to the pole and continuation

由分类结果可得,经过磁异常数据化极和延拓处理前,数据受到背景场的影响比较大,淹没了一部分的磁异常信息,致使分类结果错误大部分集中在类型四:无目标。这就造成将近一半的探测目标被遗漏,在实际应用中存在巨大风险。而类型一和二,因为形状相对接近,而导致分类结果交叉融杂。经过处理后,磁异常数据质量提高,样本数增大,虽然可看出目标遗漏仍然是主要的分类错误,但错误率大幅度降低。而类型一和类型二混淆的情况也得到改善,与类型三的错误率几近相同,说明在识别细微区别上也得到了改进,对铁磁性目标的识别正确率显著提高,证明了本方法的优势。

4 结论

本文提出了基于磁梯度张量的磁目标模式识别方法。提取磁梯度张量矩阵的9个特征量联合识别磁目标,并对磁异常数据进行化极和延拓处理,提高了数据质量,使数据特征更突出。同时将机器学习的方法引入地下磁目标识别领域,利用量子粒子群改进的支持向量机识别地下小目标的形状。本方法克服了重磁数据正、反演过程中大量的公式推导和计算,降低了对磁测数据精度的依赖,识别效果显著提高。本方法在目标识别姿态、深度方面,还有很大研究空间。