脉位编码与线性调频复合调制引信信号

谢 嘉,马 强,刘忙龙,施坤林,杨金钢,李维山

(西安机电信息技术研究所,陕西 西安 710065)

0 引言

现代战争中电磁环境复杂多变,无线电引信面临的战场环境日趋恶劣,单一体制引信已无法兼顾无线电引信对分辨力和抗干扰能力等多方面性能的要求。从目前的发展趋势来看,复合体制引信可兼顾不同探测体制的优势,无线电引信已逐渐由单一体制向复合体制转变[1]。如何合理构造复合体制引信信号,充分发挥不同探测体制优势,已成为无线电引信设计的研究热点。

传统的线性调频脉冲信号具有大的时宽带宽积[2],分辨力高；伪随机脉位调制信号具有噪声信号“图钉型”模糊函数[3],抗干扰能力强,这两种信号常被用作复合引信的组成信号。文献[4]将等周期脉冲串与线性调频相复合,可获得较高的距离分辨力,同时解决了信号处理合成带宽所需点数对运动补偿影响的问题,但等周期脉冲串不具有随机特性,抗干扰能力提升有限。文献[5]将随机噪声脉位调制与线性调频相复合,在参数选择合理的情况下,被截获概率极低,抗综合干扰能力较强。但为了获得较好的相关特性,通常需要对若干样本进行统计平均[3，6],这无形中增加了信号积累的时间,影响测距精度。

针对连续波调频、随机脉位调制单一体制引信信号及文献[4—5]所讨论的脉冲型复合信号无法兼顾分辨力、抗干扰能力和引信实时性的问题,本文提出了脉位编码与线性调频复合调制引信信号(以下简称PPC-LFM复合信号)。

1 脉位编码与线形调频复合调制引信信号

1.1 复合调制信号构造

复合调制信号构造方法可分为波形综合和波形选择两大类。波形综合法通过模糊函数最小二乘法得到最优信号波形,但该方法数学计算复杂,综合的信号不易产生和处理,所以实用性不大。波形选择法根据目标环境和战术技术要求,选择不同类型的模糊函数,然后根据各种信号的技术实现难易程度选择具体信号。本文结合波形选择法,先构造合适的复合调制引信信号波形,然后分析其模糊函数,得到复合调制引信信号特征。

1.2 脉位编码序列

Costas序列是以时频编码信号的形式提出的[7],它具有良好的模糊特性和抗干扰特性。将发射信号进行人为延时和频移后获得的本地参考信号,与接收信号重叠,遍历所有延时和频移可找到最一致的参考信号,即可获得弹目距离和速度信息。为了利用Costas序列良好的模糊和抗干扰特性,对其定义形式进行重构,将频率跳变向量替换为脉位编码向量,设计一种新的脉位编码方式,以期获得与其相似的遍历性。

考虑这样一种置换矩阵H={Hnm}(0≤n,m≤N-1),N行对应于脉冲重复周期内N个编码位置,N列对应于N个脉冲重复周期,其时间延迟置换矩阵可表示为：

H*={H(n+r)(m+s)}(0≤n,m≤N-1)

(1)

式(1)中,行延迟量r和列延迟量s满足-N+1≤r,s≤N-1且r,s同正或同负,由于其对称性,可仅考虑r,s同正的情况。

H与其延迟H*的一致程度可用非循环相关函数C(r,s)表示：

(2)

图1显示了脉位编码序列与其延迟序列置换矩阵一致性程度对比。与Costas序列不同的是,n+r和m+s超出[0,N-1]的范围,H*中部分元素不再认为是0,非循环相关函数改写为:

CPPC(r,s)=C(1)(r,s)+C(2)(r,s)

(3)

式(3)中,C(1)可由式(2)等式右端表示,C(2)表示n+r、m+s>N-1的部分：

图1 脉位编码序列与其延迟序列置换矩阵一致性对比Fig.1 Permutation matrix conformance comparison between PPC sequence and PPC delay sequence

CPPC即为脉位编码序列的非循环相关函数,对于满足式(4)的矩阵H映射到一维时间向量,就是模糊旁瓣峰值最小的脉位编码序列。

(4)

实际上,将CPPC映射到一维时间向量,则等效为脉位编码序列的非周期自相关函数,在目标多普勒变化不大的情况下,非周期自相关函数可作为序列选择与验证的准则。选取满足式(3)的序列{Cn}={1,3,4,2,5},其自相关函数如图2所示,主旁瓣比可达到20log(N),约14 dB。

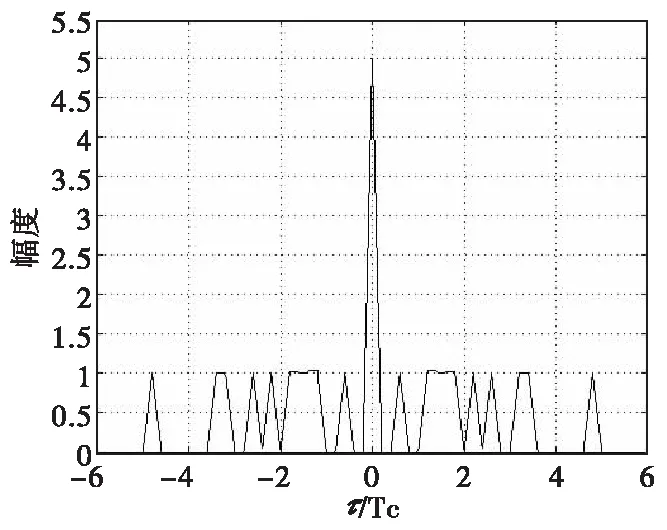
图2 脉位编码序列自相关函数Fig.2 PPC sequence autocorrelation

由上述分析可知,重构后的Costas序列单周期自相关函数具有良好的主旁瓣比,序列产生方便可控,可作为脉位编码序列。

1.3 PPC-LFM复合信号

脉位编码信号表达式为:

(5)

PPC-LFM复合信号时域表达式为:

UPPC-LFM(t)=

(6)

式(6)中,u2(t)=u1(exp)(jπkt2),为线性调频脉冲压缩信号复包络,k为调频斜率且k=B/Tm,B为调频带宽,f0为载波频率的起始频率,fn=nΔf+(Cn-1) (Δf/N),Δf为码元周期频率步进量且Δf=B/N。复合信号时域波形如图3所示。

图3 PPC-LFM复合信号时域波形Fig.3 Time-domain wave of PPC-LFM compound signal

因此,PPC-LFM复合信号复包络可表示为:

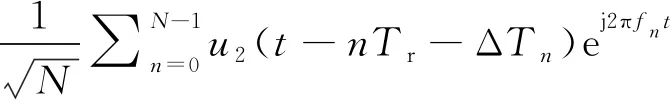
(7)

2 性能仿真验证

2.1 PPC-LFM复合信号模糊函数

模糊函数是分析无线电引信信号的有效数学工具,它利用时频分布描述了信号的全部特性,不同形式的信号尤其是复合调制信号具有其独特的模糊函数[8-9]。下面通过推导、分析PPC-LFM复合信号单周期模糊函数来揭示该信号特征及固有探测性能。

单周期模糊函数一般定义为[10]:

(8)

式(8)中,u(t)为发射信号复包络,u*(t)为u(t)复共轭,Tm为u(t)的周期。τ是相对于期望匹配滤波峰值输出的时延,fd是为滤波器设计的多普勒频率与实际接收回波的多普勒频率之间的失配频移。

将式(7)代入式(8),令t=t-nTr-ΔTn,交换积分与求和次序,则有：

χPPC-LFM(τ,fd)=

χ2(τ-(m-n)Tr-(ΔTm-ΔTn),

fd-(fm-fn))

(9)

其中χ2(τ,fd)为u2(t)的模糊函数,且有

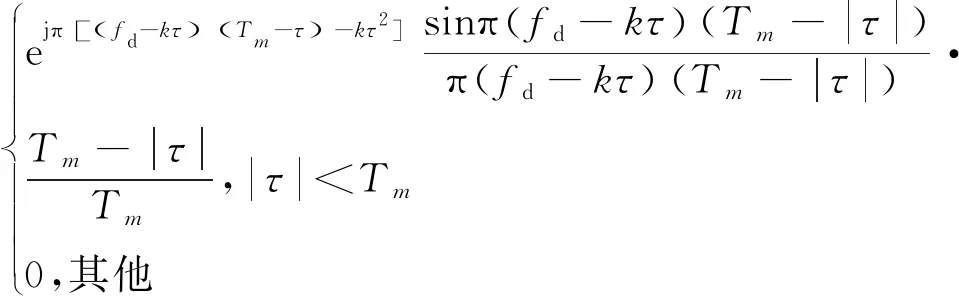
(10)

由式(9)可知,PPC-LFM复合信号模糊函数是调频脉冲信号模糊函数在时移τ=(m-n)Tr+(ΔTm-ΔTn)和频移fd=fm-fn处,被因子e-j2πfmτ·ej2π[fd-(fm-fn)](nTr-ΔTn)加权后组成的,时移量、频移量和加权因子均携带编码信息。

选取脉冲宽度Tp=100 ns、脉冲重复周期Tr=500 ns、编码序列{Cn}={1,3,4,2,5}的脉位编码信号与调频周期Tm=2.5 μs、调频带宽B=50 MHz的锯齿波调频信号相复合,根据式(9)绘制PPC-LFM复合信号模糊函数如图4所示。图4(a)为3D模糊图,图4(b)为对应的2D等高线图。

由图4可以看出,模糊图的体积分散地集中在平行于多普勒频移轴的许多带条内,每个带条都排列着许多尖峰,除了模糊图中心位置尖峰最大外,其余每个带条内的最大尖峰幅度大小相同,两者比约为14 dB,这与图2中序列自相关函数所描述的主旁瓣比一致。模糊图整体特征近似“图钉型”,其排列走向由调频参数决定,尖峰的分布间隔由编码序列决定。在尖峰排列走向以外的区域及平行的带条之间均不产生自身杂波,从而减少了对微弱回波信号的掩盖。

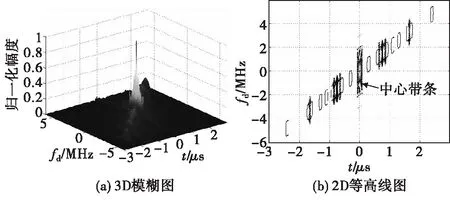
图4 PPC-LFM复合信号模糊函数Fig.4 Ambiguity function of PPC-LFM compound signal

由上述分析可知,脉冲位置受编码调制,各码元脉冲的χ2(τ,fd)在延迟轴上移动随编码信息变化,因而各码元脉冲的χ2(τ,fd)只有在m=n时,才能叠加形成峰值,即中心带条所在位置,如图4(b)中标示,此时式(9)可改写为:

χPPC-LFM(τ,fd)=

χ2(τ-(m-n)Tr-(ΔTm-ΔTn),

fd-(fm-fn))=

(11)

式(11)中,x(1)(τ,fd)为中心模糊带函数,χ(2)(τ,fd) 为旁瓣模糊带函数, PPC-LFM复合信号的距离、速度分辨力由χ(1)(τ,fd)决定,与χ(2)(τ,fd)无关。

2.2 模糊图沿时延轴垂直切割

用垂直于时延-多普勒平面、平行于时延轴的平面对χPPC-LFM(τ,fd)进行切割,其剖面反映了弹目相对速度保持不变的情况下,带有固定多普勒频率的PPC-LFM回波信号经匹配滤波器相关输出的时域波形。当fd=0时,χPPC-LFM(τ,0)即为PPC-LFM复合信号的距离自相关函数,如图5所示。

ΔR≈c/2B

(12)

脉位编码信号距离分辨力为cTp/2,显然当B≥1/Tp时,PPC-LFM复合信号拥有更好的距离分辨力。同时,主旁瓣比约为20 log(5)dB,与图2所示的序列自相关函数主旁瓣比基本一致。

图5 PPC-LFM复合信号距离自相关函数Fig.5 Range autocorrelation function ofPPC-LFMcompound signal

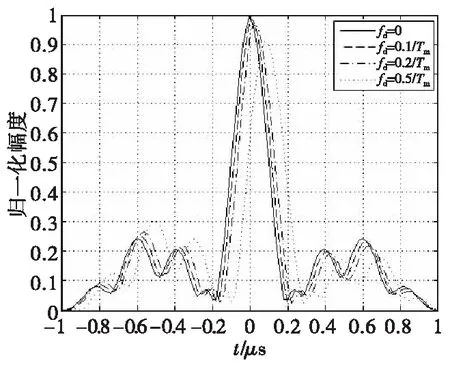
图6 不同多普勒频移下的模糊函数切割图Fig.6 Section plan of ambiguity function under different doppler frequency offset

分别对fd=0.1/Tm、fd=0.2/Tm、fd=0.5/Tm时的模糊函数进行切割,如图6所示。弹目间的相对运动使匹配滤波器相关输出发生变化,随着多普勒频率的增大,距离主峰产生正向时移,同时峰值下降,两侧旁瓣有升高有降低呈对称变化,与fd=0相比,主旁瓣比下降约2.8 dB。当调频带宽B远大于可能的多普勒频移范围时,多普勒频移引起的主峰幅值降低是很小的,也就是说匹配滤波器的信噪比损失很小,同时时延分辨力几乎没有变化,可以说距离分辨力未受影响,由此可知,PPC-LFM复合信号是多普勒不敏感信号,这有助于简化引信信号处理系统。

2.3 模糊图沿频移轴垂直切割

用垂直于时延-多普勒平面、平行于频移轴的平面对χPPC-LFM(τ,fd)进行切割,其剖面反映了弹目间距离保持不变的情况下,一定时延下的PPC-LFM回波信号经匹配滤波器相关输出的频域波形。当τ=0时,χPPC-LFM(0,fd)即为PPC-LFM复合信号的速度自相关函数,如图7所示。

Δv≈λ/2Tm

(13)

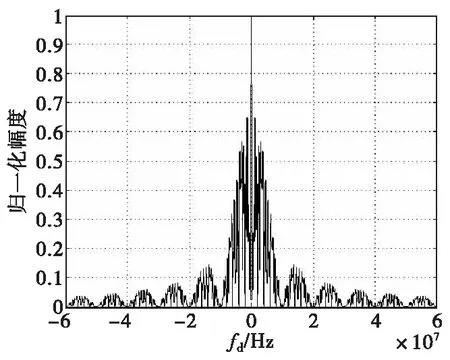
图7 PPC-LFM复合信号速度自相关函数Fig.7 Speed autocorrelation function of PPC-LFMcompound signal

这与线性调频信号、频率步进脉冲串信号的速度分辨力基本是一样的。

单周期信号的多普勒分辨率对于引信速度信息提取往往是不够的,这里考虑对回波信号进行M个周期积累,M周期模糊函数为[11]：

(14)

由式(14)可知周期信号的模糊函数与延时τ无关,且调制周期数越大,速度分辨力越好,即:

ΔvM≈λ/2MTm

(15)

图8显示了一个脉冲周期对应频率范围内单周期与5周期速度自相关函数对比。经过5个周期积累后速度分辨力提升5倍,同时多普勒旁瓣和主峰一样变窄,基底出现更小的旁瓣,特征类似线性调频信号速度自相关函数。因此,对PPC-LFM复合信号目标回波进行多周期积累,能够改善速度分辨力,有利于弹目相对速度信息提取。

分别对τ=0.6Tr，τ=1.1Tr，τ=1.84Tr，τ=2.6Tr时的模糊函数进行切割,如图9所示。随着时延的增大,速度主峰产生正向时移,峰值衰减不小于14 dB,主峰随时移衰减规律与编码序列自相关函数特征有关,峰值越低主峰展宽越大。由此可见,PPC-LFM复合信号适于在弹目距离变化不大的某一时段对相对速度信息进行提取。

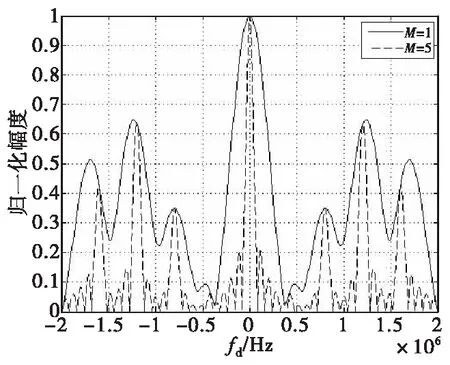
图8 单周期与5周期速度自相关函数对比Fig.8 Comparison of speed autocorrelation function between single period and 5 period

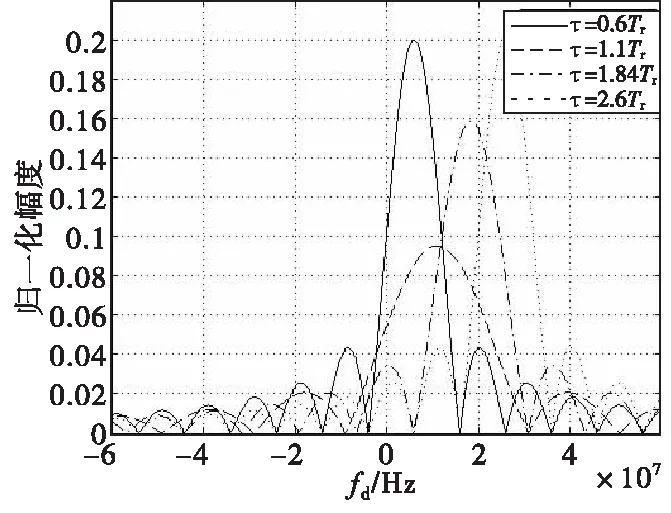
图9 不同时延下的模糊函数切割图Fig.9 Section plan of ambiguity function underdifferent delay

2.4 模糊图平行切割

无线电引信工作时间短、作用距离近,其抗干扰性能评定及方法检验不同于雷达,目前仍处于探索阶段。这里基于有源干扰机理,使用模糊函数平行切割的截面积大小作为衡量其固有抗干扰性能的测度标准[12]。对发射信号模糊函数在一定高度h下进行平行于底面的切割得到截面A,该高度h的选择与引信体制、接收机所采用的抗干扰措施及信号处理方法有关,截面A称为不分辨区域。不分辨区域A的面积SA作为无线电引信固有抗干扰性能的量度,SA越小,引信抗干扰性能越强。

考虑弹目接近速度及最小处理时间,在多普勒频移1 MHz、时延一个周期Tm内,对模糊图进行-3 dB平行切割,图10显示了PPC-LFM复合信号与线性调频信号不分辨区域面积随等效带宽变化曲线对比。在相同等效带宽情况下,PPC-LFM复合信号不分辨区域面积小于线性调频信号,且等效带宽越小差距越大,随着编码位数的增加,PPC-LFM复合信号不分辨区域面积减小,与之周期对应的不同调制频率的线性调频信号面积变化很小。图11显示了PPC-LFM复合信号不分辨区域面积随等效带宽增加而减小,但其与线性调频信号相比变化不明显。由此可见,PPC-LFM复合引信固有抗干扰能力强于线性调频引信,编码位数越大,抗干扰能力越强。

图10 PPC-LFM复合信号与线性调频信号SA对比Fig.10 Comparison of SA between PPC-LFM signal and LFM signal

由仿真验证可知,PPC-LFM复合信号在调频带宽大于脉宽对应带宽时,保持了线性调频引信良好的距离、速度分辨力,增加调频带宽可提高距离分辨力,增加调制周期可提高速度分辨力且增大不模糊距离,但此时调制频率下降会影响多普勒信号提取,可考虑适当处理M个周期来提升速度分辨力为原来的M倍。N个码元的单周期自相关函数主旁瓣比可达20 log(N)dB,即无需若干样本积累便拥有一定的伪随机特征,但码元数增加同样使调制周期变大且平均发射功率降低,此时需根据战技指标权衡考虑码元数的选取。在一定距离和速度范围内、相同调制带宽情况下,PPC-LFM复合信号固有抗干扰能力优于线性调频信号。同时,PPC-LFM复合信号是多普勒不敏感信号,这有助于简化信号处理系统。

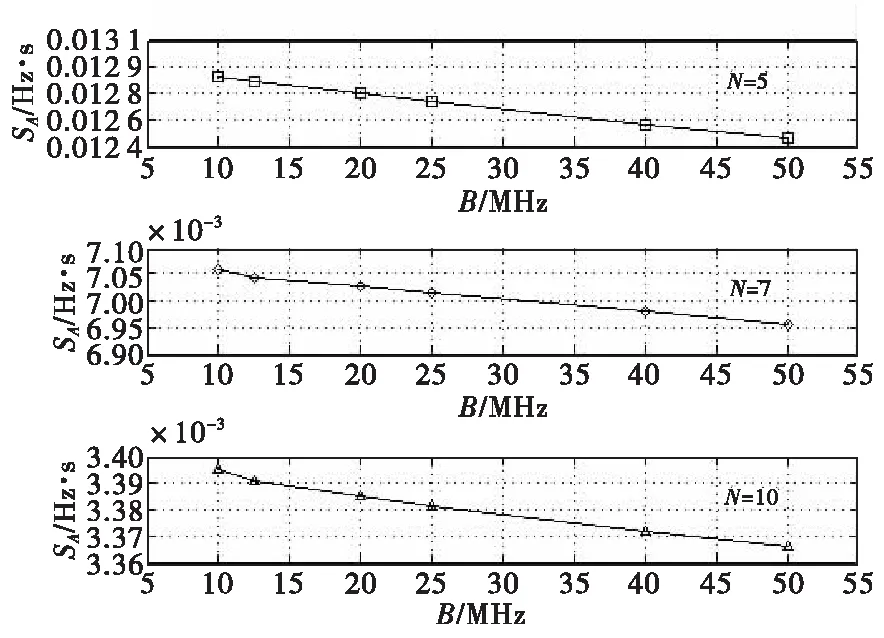
图11 不同编码位数的PPC-LFM复合信号SA对比Fig.11 SA comparison of PPC-LFM signal with different coded number

3 结论

本文提出了脉位编码与线性调频复合调制引信信号。利用Costas序列良好的模糊特性和抗干扰特性重构了一种新的脉冲位置编码方式,结合波形选择法,构造了脉位编码与线性调频复合引信信号。仿真结果表明,脉位编码与线性调频复合调制引信信号在参数选择合理的情况下能够保持线性调频信号良好的距离、速度分辨力,无需若干样本积累即拥有一定的伪随机特征,在一定距离和速度范围内,固有抗干扰能力优于线性调频信号,可应用于工程实践。