奇异值分解和EEMD的非线性振动信号降噪方法
2019-08-28刘树聃陈知行
刘树聃,陈知行
(1.许昌市耕新信息科学研究院,河南 许昌 461000;2.许昌职业技术学院航空工程学院,河南 许昌 461000;3.北京理工大学自动化学院, 北京 100081)
0 引言
机械运转时干扰复杂,常常会淹没机械真实状态信息,极大影响了信号真实信息的解读,给机械设备状态监测造成很大阻碍,并且机械系统因其复杂结构具有非线性的动力学行为,其信号具有功率宽带性和伪噪声性,噪声和信号频带部分甚至全部重叠,使得传统的降噪方法难以取得较好效果[1]。
目前,常用的非线性降噪方法有小波变换、经验模态分解(Empirical Mode Decomposition, EMD)等,小波变换降噪效果受到小波基、分解层数和阈值这三要素影响较大,且阈值处理过程会导致有用信号被剔除,降噪效果不太理想[2]。EMD在受到脉冲强干扰的情况下,其分解出来的本征模态分量(Intrinsic Mode Function,IMF)会发生畸变,导致信号失真[3-4],且EMD本身存在一些不足,如模式混叠、端点效应、停止条件等[5]。文献[6]提出了集合经验模态分解方法,能有效地抑制模式混叠。实测的非线性振动信号往往存在较强的随机噪声和脉冲干扰,尤其低信噪比条件下,信号几乎被噪声淹没。以上单一的方法很难有效地将有用细节从强干扰中提取出来。文献[7]提出基于奇异值分解(Singular Value Decomposition,SVD)和EMD的信号降噪方法,但是该方法无法有效抑制脉冲噪声和模式混叠现象。文献[8]提出了利用Savitzky-Golay(SG)滤波方法对海杂波信号经EEMD分解后噪声占主导作用的IMF分量进行降噪处理,SG滤波算法可以有效抑制脉冲噪声,但是对于低频含噪信号比较有效,若是处理噪声主导的高频含噪信号会导致部分有用细节的流失。文献[9]提出一种小波包降噪算法与 EMD 解相关算法相结合的数据处理方法,能够同时有效抑制模态混叠现象和消除白噪声干扰,但是缺乏抑制脉冲噪声的手段。以上降噪方法无法同时实现既抑制白噪声和脉冲干扰又能减少有用信号失真这一理想效果。为此,本文提出基于SVD和EEMD的非线性振动信号降噪方法,充分利用EEMD叠加白噪声的预处理手段,有效抑制脉冲噪声和模式混叠,且分解后的信号提取出趋势项可以提高奇异值差分谱方法选择重构点的自适应性[7],实现SVD和EEMD的优势互补,提高降噪效果。
1 EEMD和SVD基本原理
1.1 EEMD基本原理
利用EMD对信号进行去噪处理时,由于相邻本征模态分量或者同一本征模态分量频率相近的噪声和信号会发生能量渗透,导致信号和噪声无法完全筛分,影响去噪效果。为此,在利用EMD处理信号时,先对信号叠加M零均值的白噪声[6],目的是使白噪声均匀分布在各个频段上,可以引导信号自适应分布到合适的频段上,克服了极值点分布不均匀的缺陷,并且,多次叠加白噪声然后取平均,可以抵消部分噪声的干扰,减少EMD过程中噪声引起的异常事件。因此,EEMD就是叠加白噪声预处理后的经验模式分解[6],具体步骤如下:
1) 对原始信号x(t)中叠加M(M>1)次均值为0,均匀分布的高斯白噪声ni(t),i=1,2,…,M,即:
xi(t)=x(t)+ni(t)
(1)
2) 对预处理后的xi(t)进行EMD处理,得到N个IMF记为aij(t),j=1,2,…,N,ri(t) 表示余项。其中,aij(t)表示经过叠加第i次高斯白噪声后,再经EMD处理得到的第j个IMF。
3) 由于噪声时零均值均匀分布,因此,将式(1)、2)步处理后得到的IMF进行M次平均运算,就可以消除预处理过程中叠加的白噪声的影响,EEMD处理得到的IMF为:
(2)
式(2)中,aj(t)表示对原始信号进行EEMD分解后所得的第j个IMF分量。
1.2 SVD信号降噪方法
对于信号x={xi},i=1,2,…,N,可以构造如下Hankel矩阵:
(3)
对H进行奇异值分解,得到:
H=USVT
(4)
式(4)中,U、V为正交矩阵,VT为V的转置,S为由奇异值构成的对角矩阵。其奇异值存在如下关系:σ1>σ2>…>σk≫σk+1>σk+2>σr。其中,σk为奇异值分界得到的第k个奇异值,k=1,2,…,r,r为矩阵H的秩,≫表示从第k+1个奇异值起,后续奇异值明显小于前k个奇异值,因此可以将第k+1起后续的奇异值看作是噪声分量对应的奇异值[10]。因此奇异值分解降噪的关键在于重构个数k的选择。
文献[11]定义奇异值差分谱为:
di=σi-σj,j=i+1,i=1,…,q
(5)
式(5)中,q=min(N-n+1,n)-1。
记差分谱序列D=(d1,d2,…,dq)。D的前k个奇异值为信号的真实分量对应的奇异值,第k+1个奇异值起为噪声对应的奇异值,则D的第k个元素dk为差分谱序列的最大峰值,即:
k=argmax{peak(di):i=1,…,q}
(6)
式(6)中,peak(di)表示di的峰值。
选择前k个奇异值即可重构原信号,在实际应用中,对含有较强趋势项的信号进行降噪时,奇异值差分谱方法不能有效选择奇异值[7]。
2 SVD-EEMD信号降噪模型建立
EEMD在对信号降噪时,对本证模态分量阈值处理,难免会造成高频噪声遗留,低频有用信号流失[6],而SVD则是有效秩次的确定易受到信号趋势项的影响[7]。SVD-EEMD降噪模型的主要效用:一是有效抑制非线性机械振动中的脉冲噪声;二是有效抑制EMD模式混叠效应;三是利用EEMD提取信号趋势项,提高SVD奇异值选择的自适应性,且克服简单对本证模态分量阈值处理造成不理想的降噪效果这一缺陷。具体实施步骤如下:
1) 对原始信号叠加M(M>1)次均值为0,均匀分布的高斯白噪声;
2) 对预处理后的信号进行EMD处理;
3) 选择时间尺度,提取信号的趋势项,将信号分为a(t)和tr(t)两部分;
4) 利用SVD对a(t)进行降噪处理,采用奇异值差分谱确定需重构的奇异值个数;
5) 将处理后得到的a′(t)和趋势项叠加即为降噪后的信号。
3 验证分析
3.1 EMD和EEMD比较分析
引起模式混叠的主要原因是受外部异常事件的影响,如间断信号、脉冲干扰和白噪声等。为了验证受干扰条件下非线性振动信号EEMD分解的抑制混叠效应能力,本文以叠加15 dB的Lorenz时间序列和Gauspuls脉冲分量组成的信号进行仿真分析,其中Gauspuls脉冲干扰的中心频率fc=1 000 Hz,相对带宽bw=0.5。图1(a)为原始信号;图1(b)为仿真信号的EMD分解结果,包括四个IMF分量和一个余项res。图中在干扰附近(箭头所标位置)是干扰和Lorenz序列的模式混叠,分布有两者的特征时间尺度,并且与原始信号相比,发生混叠处原始信号都存在明显脉冲干扰。因此,在去噪的同时会导致部分有用信号的遗失。图1(c)为仿真信号的EEMD分解结果,加入0.4倍信号标准偏差的高斯白噪声,加入次数M=100,可以看出,分解结果并未出现明显的模式混叠。图2为仿真信号EMD和EEMD与原始信号的重构误差,可以看出EMD重构误差e1=0.227 1明显大于EEMD重构误差e2=0.137 0,说明了异常事件使原始信号发生畸变,导致了信号失真,进一步证实了EEMD的优势。
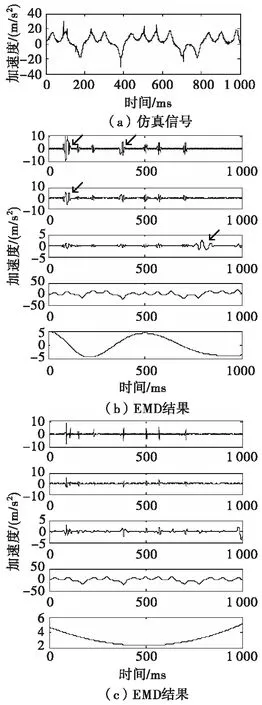
图1 仿真信号的EMD和EEMD结果Fig.1 EMD and EEMD results of simulation signal
3.2 降噪方法对比分析
以信噪比为-5 dB的Lorenz时间序列为例,并叠加Gauspuls脉冲干扰对本文所提方法的必要性进行分析,干净的Lorenz时间序列和叠加干扰的含噪序列如图3所示。
按照降噪模型实施步骤,首先对含噪信号进行EEMD处理,如图4所示。为了验证趋势项对SVD差分谱选取需重构的奇异值个数的影响,分别利用SVD对原始信号和EEMD分解后去除趋势项的剩余部分进行处理,结果如图5所示。受趋势项的影响,图5(a)中箭头所指位置,奇异值差分谱最大值出现在第一个位置,将第一个奇异值重构后后导致有用细节的过量。图5(b)中奇异值差分谱出现在第2个位置,而在最大值之后,奇异值差分谱的值远小于最大值,且分布比较均匀,因此信号经过EEMD处理后消除了趋势项对SVD奇异值选择的影响,分析结果和文献[7]吻合。
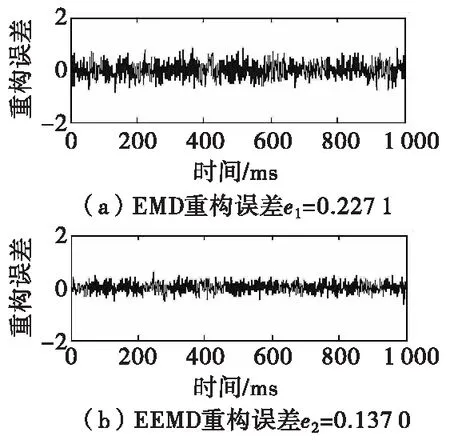
图2 EMD和EEMD重构误差Fig.2 Reconstruction error of EMD and EEMD
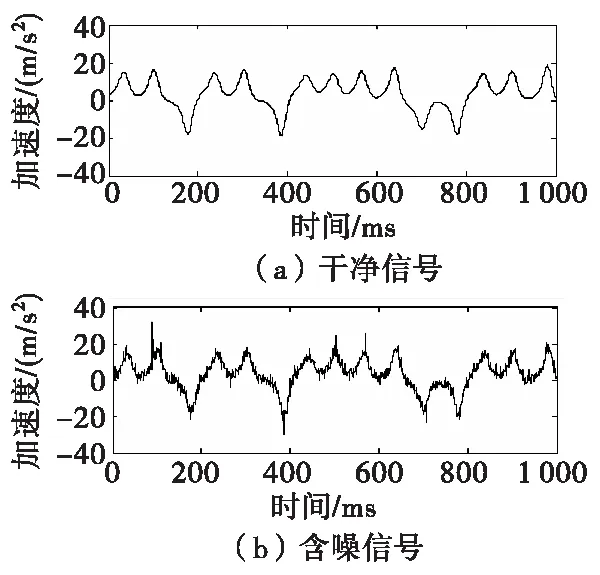
图3 Lorenz时间序列Fig.3 Lorenz time series
为了更加直观地比较降噪效果,分别利用SVD、EEMD、SVD-EMD[7]和SVD-EEMD对含噪Lorenz信号进行降噪处理,结果如图6所示。图6(a)中,由于趋势项的影响,单一使用SVD降噪会导致原始信号失真,如图中箭头所示;图6(b)中,传统EEMD对高频分量阈值处理后不可避免遗留部分噪声,从而导致降噪后信号粗糙;图6(c)中,白噪声得到了有效抑制,并且信号比较平滑,但是对脉冲噪声的抑制效果不明显,如图中箭头所示;图6(d)中,本文方法降噪后信号中白噪声和脉冲噪声都得到了有效抑制。表1给出了四种方法去噪后信号的信噪比(SNR)和均方误差(MSE),可以看出,本文方法降噪效果最优,降噪后信号的信噪比提高到了18.154 7 dB。
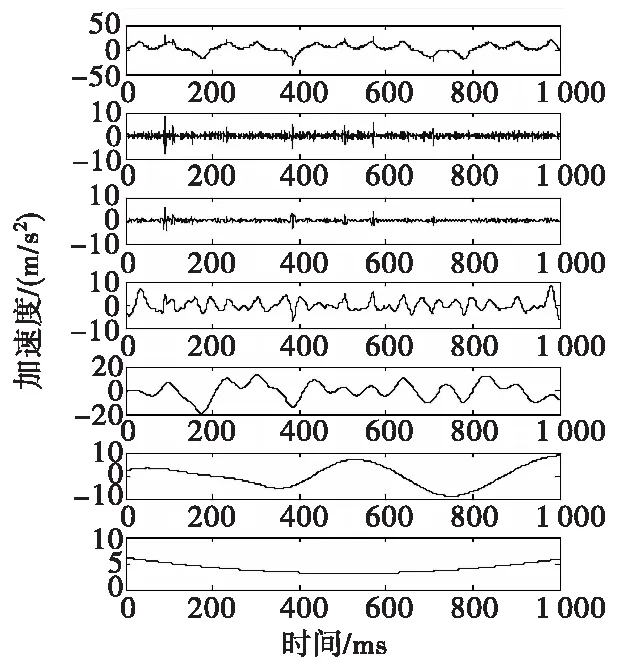
图4 EEMD处理结果Fig.4 The EEMD result of simulation signal
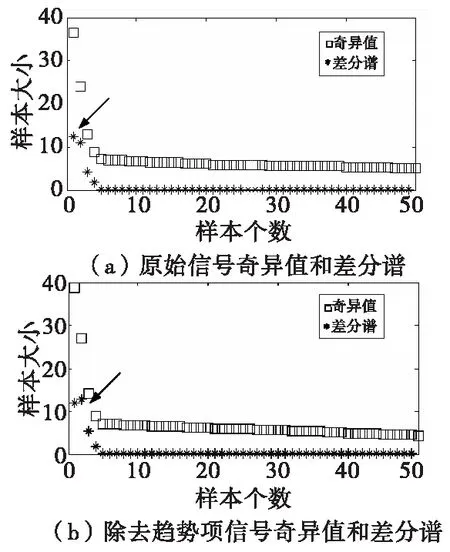
图5 信号奇异值和差分谱Fig.5 Signal singular value and difference spectrum
信噪比反应去噪能力的大小,均方误差的物理意义是表示去噪后信号和原始信号的平均偏离程度,求解信噪比和均方误差的公式为:
(7)
(8)
式(7)、式(8)中,x′(n)表示去噪后的序列,x(n)为原始时间序列,var(·)表示方差,x′(n)-x(n)表示信号中的剩余噪声。
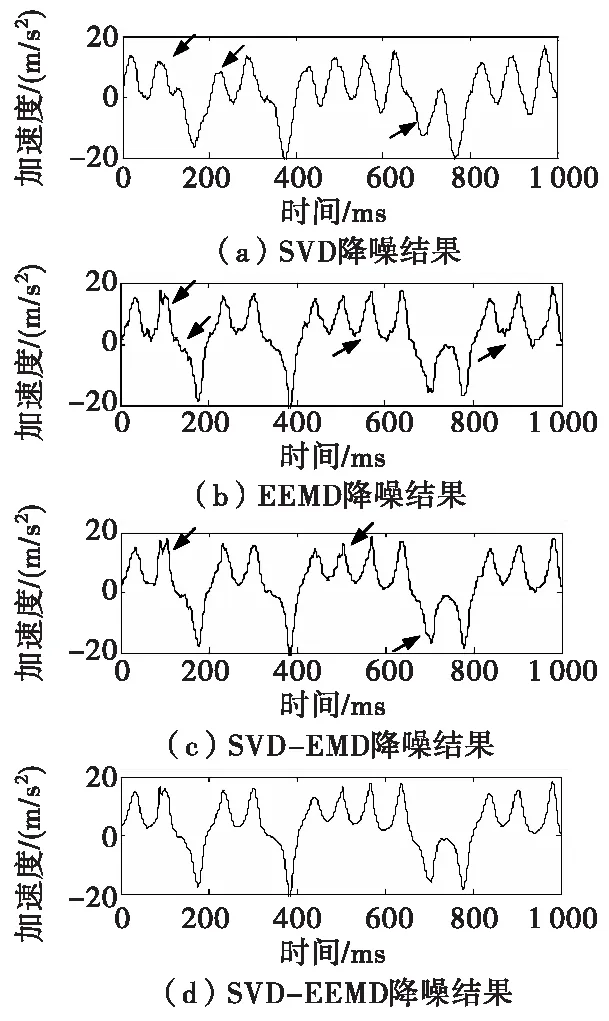
图6 四种方法降噪效果Fig.6 The noise reduction effect of four methods
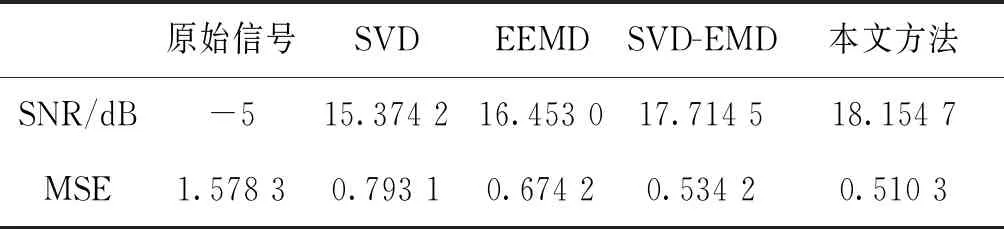
原始信号SVDEEMDSVD-EMD本文方法SNR/dB-515.374 216.453 017.714 518.154 7MSE1.578 30.793 10.674 20.534 20.510 3
3.3 实测振动信号处理
实测信号由分段隔振系统产生[12],设计的初衷是对振动控制进行分析。在振动控制领域,对振动信号的识别和预测有着至关重要的作用,而噪声的存在会极大干扰识别和预测效果,从而无法准确掌握振动趋势,无法给出相应的振动控制策略。考虑到采集的信号是非线性,且易受到复杂外部干扰,因此有效的降噪手段对振动信号进行下一步分析处理至关重要。为模拟被隔振设备,设计一个上层质量块,同时利用激振器产生一定的激励力模拟设备在工作时的状况。硬件部分还包括信号采集装置(NIPXI-10420)、功率放大器(YE5873)、激振器(JZK-40)等,信号通过加速度传感器采集,信号发生器为本试验提供谐波信号,经功率放大器放大后驱动激振器,试验过程中,通过改变增益可以调节整个非线性隔振系统的参数,模拟设备的不同工况。试验装置如图7所示。

图7 实验装置图Fig.7 The figure of experimental setup
激励频率f=20 Hz时,底层基座采集的时间序列图如图8(a)所示,数据长度为3 000。图8(b)、图8(c)分别为SVD-EMD和SVD-EEMD的去噪结果。由于原始信号为机械式振动信号,其信号和噪声未知,不能利用信噪比和均方误差进行定量比较,但是白噪声不具备相关性,其自相关系数远远小于信号[13],因此,可以利用3种方法去噪后的自相关函数值评价去噪效果。
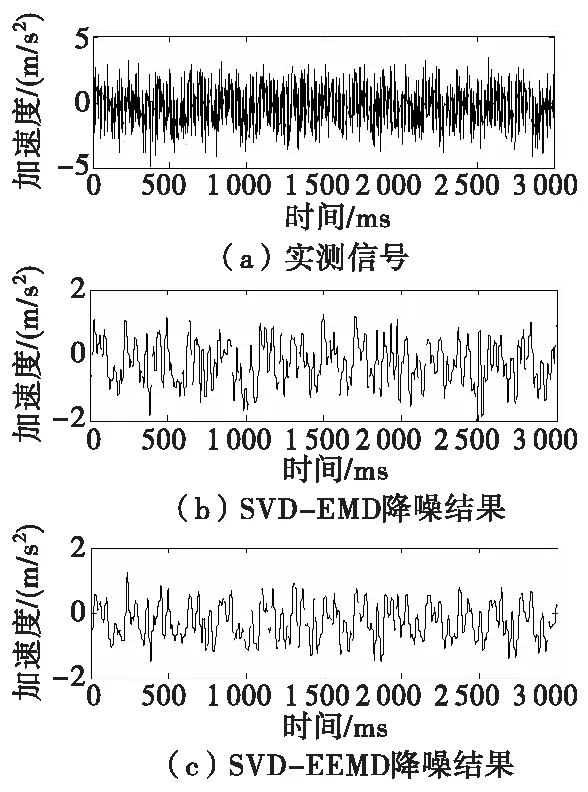
图8 实测信号降噪结果Fig.8 De-noising results of measured signal
两种方法去噪前后的部分自相关函数值如图9所示。图中,“△”表示SVD-EEMD的自相关函数曲线,“---”表示SVD-EMD的自相关函数曲线,“—”表示原始信号的自相关函数曲线。可以看出,原始信号受到噪声的干扰,其自相关函数值相比去噪后要小很多,而本文所提方法降噪后序列的自相关函数值最大,说明噪声抑制效果最明显,进一步展现了其降噪的优越性,也证明了本文方法可以为工程实测信号进一步分析处理提供了有效的预处理手段。
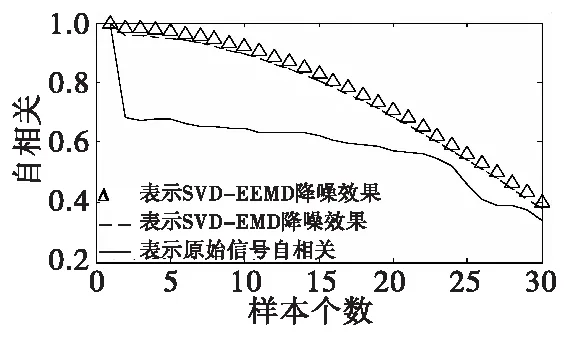
图9 降噪前后信号的自相关函数曲线图Fig.9 Autocorrelation function of the signal
4 结论
为了有效抑制工程实际中常见的白噪声和脉冲噪声,本文提出了基于SVD-EEMD降噪方法。该方法通过EEMD提取趋势项和抑制脉冲干扰,提高SVD奇异值选择的自适应性,然后利用SVD进一步增强降噪效果。通过仿真信号和实测非线性振动信号分析,结果表明,所提方法可以有效实现SVD和EEMD优势互补,在抑制模式混叠和脉冲干扰的同时,减少趋势项对SVD奇异值选择的影响,大大提高了降噪效果,减少了有用信号失真,为工程实测信号进一步分析提供有效预处理手段,具有良好的工程应用前景。
