双基地MIMO雷达三维空间目标参数估计算法

李云成,崔 琛,龚 阳

(国防科技大学电子对抗学院,安徽 合肥 230037)

0 引 言

多输入多输出(MIMO)雷达在目标检测、参数估计、杂波抑制等方面具有诸多优势[1],引起了国内外学者的高度关注。在双基地相干MIMO雷达参数估计方面,文献[2-5]分别通过Capon二维谱峰搜索、ESPRIT、传播算子以及MUSIC等方法实现了目标收发角估计。考虑运动目标的多普勒效应,文献[6-11]分别提出基于多维ESPRIT、平行因子分析、最大似然等方法的目标收发角和多普勒频率估计算法。然而,上述算法收发阵列均采用线型配置,只能估计出二维平面中目标的收发角及多普勒频率,而无法确定三维空间中的目标位置。与线型阵列相比,交叉阵列能够有效辨识二维收发角,结合收发基地的距离,则可以确定目标的空间位置。研究表明,在相同条件下,L型阵列的性能优于其他几种交叉阵列[12]。因此,本文主要研究L型双基地MIMO雷达目标参数估计问题。

目前,关于L型双基地MIMO雷达的研究较少。文献[13]利用投影矩阵法实现了适用于L型双基地MIMO雷达的目标参数估计算法,但该算法在信噪比较低时,参数估计性能较差。文献[14]通过对接收数据求自相关矩阵并对该矩阵进行特征值分解等操作,实现了三维空间中目标的收发角估计,但该算法假设噪声方差已知,而该假设通常并不成立。文献[15-18]分别提出基于ESPRIT、迭代最小二乘、传播算子以及互相关矩阵的目标多维角度估计算法,算法均无需已知噪声的方差,且实现了目标参数的自动配对。此外,文献[19-20]对ESPRIT算法加以改进,实现了目标多维角度及多普勒频率的估计。然而,上述关于L型双基地MIMO雷达的算法均只在收发阵列采用均匀配置,且目标散射系数已知或服从Swerling-I模型的条件下适用。当采用非均匀配置或目标散射系数服从Swerling-Ⅱ模型时,算法性能将明显下降甚至失效。针对该问题,本文提出基于平行因子分析的非均匀线型发射阵列和非均匀L型接收阵列的双基地MIMO雷达目标参数联合估计算法。

1 信号模型

非均匀线型发射阵列和非均匀L型接收阵列的双基地MIMO雷达如图1所示,发射阵元与y轴上的接收阵元配置在同一直线上。发射阵元M个,位置t=[t1,t2,…,tM]T·λ/2,其中tm(m=1,2,…,M)为自然数,且参考阵元位置t1=0,λ为载波波长；接收阵元2N-1个,位置rx=[r1,r2,…,rN]T·λ/2,ry=[r1,rN+1,rN+2,…,r2N-1]T·λ/2,其中rn(n=1,2,…,2N-1)为自然数,且参考阵元位置r1=0。

图1 非均匀线型发射L型接收的双基地MIMO雷达Fig.1 Non-uniform linear transmitting L-shaped receiving bistatic MIMO radar

假设目标相对接收基地的坐标为(x,y,z),且x,z>0,则由图可知,目标位置与空间角(θ,φ,γ)、(θ,ψx,ψy)一一对应,且φ,γ和ψx,ψy满足如下关系:

(1)

本文用(θ,φ,γ)表示三维空间目标的收发角。为方便叙述,称其为目标三维收发角。其中θ(0°<θ<180°)为发射角；φ(-90°<φ<90°)和γ(0°<γ<90°)为二维接收角。为方便描述,称φ为方位角,γ为俯仰角。发射阵元同时发射一组相互正交的窄带相位编码信号,在一个脉冲重复周期T内该信号的矩阵形式:S=[s1,s2,…,sM]T∈M×L,满足SSH/L=IM,其中sm(m=1,2,…,M)为第m个阵元发射信号；L为相位编码个数；I#表示#×#维单位阵；(·)T、(·)H分别表示矩阵(矢量)的转置和共轭转置。

假设远场存在P个互不相关的点目标,且在Q个脉冲重复周期内其三维收发角及多普勒频率保持不变,分别为θ=[θ1,θ1,…,θP]T,φ=[φ1,φ2,…,φP]T,γ=[γ1,γ2,…,γP]T,f=[f1,f2,…,fP]T。目标散射系数服从Swerling-Ⅱ模型,即目标回波系数在脉冲与脉冲之间是独立的。则第q(q=1,2,…,Q)个脉冲重复周期收到的回波信号可表示为:

R(q)=[BΛd(q)ATS+W(q)]∈(2N-1)×L

(2)

式(2)中,矩阵A=[a1,a2,…,aP]∈M×P,其中ap=[1,e-jπt2cosθp,…,e-jπtMcosθp]T为第p个目标的发射导向矢量；B=[b1,b2,…,bP]∈(2N-1)×P,其中bp=[1,e-jπr2cosφpcosγp,…,e-jπrNcosφpcosγp,e-jπr(N+1)sinφpcosγp,…,e-jπr(2N-1)sinφpcosγp]T为第p个目标的接收导向矢量；Λd(q)=[diag(d(q))]∈P×P为对角阵,其中diag(·)表示对角化操作,d(q)=[β1(q)ej2π(q-1)f1T,…,βP(q)ej2π(q-1)fPT],βp(q)为第p个目标在第q个脉冲重复周期的散射系数；W(q)为噪声项。

(3)

图2 K级非均匀延迟器Fig.2 K level non-uniform retarder

对接收数据x(q)进行K级非均匀延迟处理,如图2所示。延迟时间u=[u1,u2,…,uK]T·τ,且max(μk)τ≤QT,其中uk(k=1,2,…,K)为自然数,初始时间u1=0,τ为单位延迟时间,max(·)表示取最大值运算。则第k级延迟器的输出为:

(4)

将K级延迟器输出的矢量合并,可得时空信号模型:

(5)

式(5)中,y(q)表示第q个快拍；矩阵C=[c1,c2, …,cP] ∈K×P,其中cp=[1,ej2πu2τfp,…,∈K×1为第p个目标的时域导向矢量；A,B为目标的空域导向矩阵；n(q)=[wT(q),wT(q+u2τ),…,wT(q+uKτ)]T为高斯白噪声。

将Q个快拍数据合并得:

(6)

式(6)中,D=[dT(1),dT(2),…,dT(Q)]∈Q×P；N=[n(1),n(2),…,n(Q)]为高斯白噪声。可见,对目标三维收发角和多普勒频率的估计可转化为对导向矩阵A,B,C的估计。

2 基于平行因子分析的参数估计算法

2.1 四线性平行因子分析法

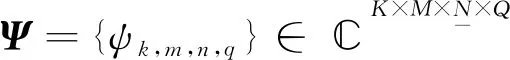
(7)

步骤3 计算代价函数

判断|γ(i)-γ(i-1)|<Δ(Δ为足够小的正数),成立,则停止计算；不成立,则令迭代次数i=i+1,并转到步骤2。式中‖·‖F表示矩阵Frobenius范数。

2.2 目标参数联合估计

为提高目标参数估计精度,构造虚拟导向矩阵:

(8)

为进一步扩展虚拟孔径,接收阵列x、y方向同样采用最小冗余配置,以表1中4元阵为例,即rx=ry=[0,1,4,6]T·λ/2,则接收导向矢量bp=[1,e-jπcosφpcosγp,e-jπ4cosφpcosγp,e-jπ6cosφpcosγp,e-jπsinφpcosγp,e-jπ4sinφpcosγp,e-jπ6sinφpcosγp]T,通过差分同置结构最终产生43个独立位置的虚拟阵元,如图3所示。为简化算法,本文仅利用x、y轴上的独立位置虚拟阵元(25个),估计目标的2维接收角。

表1 最小冗余阵列

图3 虚拟阵元位置示意图Fig.3 The figure of virtual array elements position

(9)

(10)

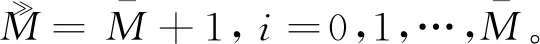
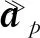
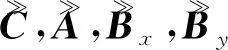
3 运算量分析

4 仿真实验与分析

本节首先验证所提算法的有效性,之后与文献[19]、文献[20]算法(分别记为“RX-ESPRIT”和“LS-ESPRIT”)进行参数估计精度比较。假设发射信号的载频为300 MHz,单脉冲内编码数L=128,脉冲重复周期T=5 ms,单位延迟时间τ=4 ms,发射阵列、接收阵列(x方向与y方向)和多级延迟器均采用表1中4元最小冗余配置方式,即t=[0,1,4,6]T·λ/2,rx=[0,1,4,6]T·λ/2,ry=[0,1,4,6]T·λ/2,u=[0,1,4,6]T·τ。与此对应,为使RX-ESPRIT和LS-ESPRIT算法有效,对这两种算法仿真时,收发阵列均采用阵元间距为λ/2的L型7元均匀配置,且假设目标散射系数为常数1。分别进行如下实验。

可见,本文算法能够对多个目标的三维收发角和多普勒频率进行有效估计,同时本文算法估计的星座点分布相对集中,在一定程度上反映了算法的稳健性。

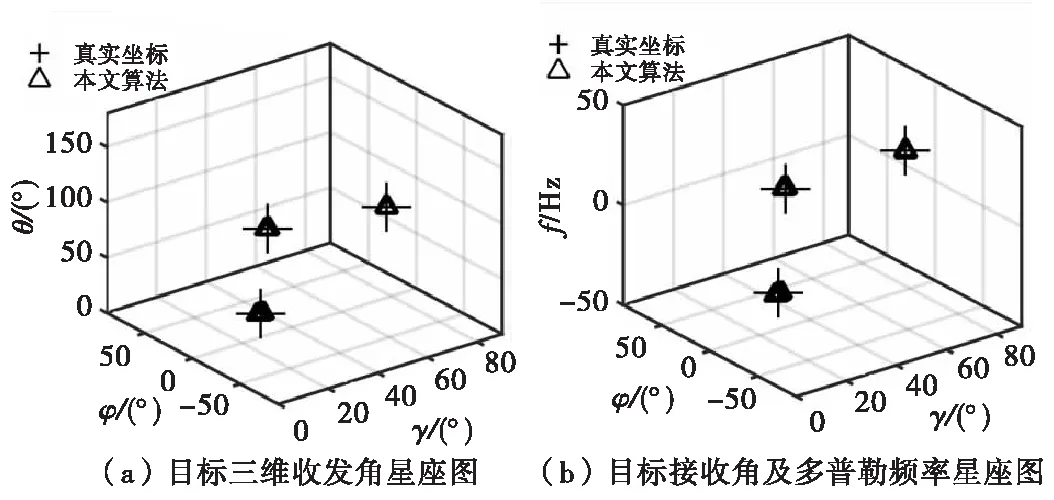
图4 目标估计参数的星座图Fig.4 The constellation of targets estimation parameters

实验2 不同信噪比条件下参数估计性能 改变信噪比(SNR=-10～20 dB),其他条件与实验1相同,分别采用RX-ESPRIT算法、LS-ESPRIT算法和本文算法估计目标参数,进行500次Monte Carlo实验,结果如图5所示。

图5 不同信噪比下参数估计的均方根误差Fig.5 The root mean square error of the parameter estimation under different SNR

可见,本文算法能够以较少的阵元(共11个)实现目标三维收发角及多普勒频率的估计,且估计精度优于采用14个阵元的RX-ESPRIT和LS-ESPRIT算法。分析原因:1)本文采用最小冗余线型发射L型接收的配置方式,降低了系统配置需求。2)本文通过构造虚拟导向矩阵和降噪处理,提高了孔径扩展效率,进而提高了参数估计精度。因此,本文算法系统配置需求较低且参数估计精度更优。

实验3 不同快拍数条件下参数估计性能 改变快拍数(Q=5～30),其他条件与实验1相同,分别采用RX-ESPRIT算法、LS-ESPRIT算法和本文算法估计目标参数,进行500次Monte Carlo实验,结果如图6所示。

图6 不同快拍数下参数估计的均方根误差Fig.6 The root mean square error of the parameter estimation under different snapshots

可见,本文算法能够在少快拍数条件下对目标参数进行有效估计,且估计精度优于RX-ESPRIT和LS-ESPRIT算法。分析原因:RX-ESPRIT和LS-ESPRIT算法在运算过程中会损失一定的时域(快拍)孔径,而本文通过延迟处理和构造虚拟时域导向矩阵等操作,提高了时域孔径扩展效率。因此,本文算法在少快拍条件下仍然有效。

5 结论

本文建立了非均匀线型发射阵列和非均匀L型接收阵列的双基地MIMO雷达信号模型,提出了基于平行因子分析的目标三维收发角及多普勒频率联合估计算法。该算法借鉴平行因子分析法和虚拟导向矩阵构造法在参数估计方面的优势,通过少量快拍即可实现目标参数高精度联合估计。仿真结果表明,与传统算法相比,该算法所得参数自动配对且在目标散射系数服从Swerling-Ⅱ模型的条件下依然有效,同时,该算法实现了孔径的高效扩展,提高了参数估计精度,降低了系统配置需求。