基于路侧单元协助的VANET同步多信道MAC协议
2019-08-27
(1.中国电子科技集团第三十四研究所, 广西桂林541004;2.桂林电子科技大学信息科技学院, 广西桂林541004;3.桂林电子科技大学信息与通信学院, 广西桂林541004)
0 引言
近年来,机动车数量快速增长,道路交通系统面临诸多挑战,促使车载自组织网络(vehicular ad-hoc networks,VANET)得到了广泛研究和发展[1-2]。其中,IEEE1609.4标准[3]为VANET提供了多信道接入服务,其目的是保证安全信息的可靠传输以及非安全信息的传输效率最大化。然而,IEEE1609.4标准规定所有节点均需要通过竞争的方式访问业务信道(service channel,SCH)和控制信道(control channel,CCH),而且有限的CCH间隔满足不了大量节点的密集竞争访问。特别是在车辆节点密集环境下,较小的CCH访问碰撞概率是决定VANET MAC协议性能的关键。因此,为研究降低访问CCH的碰撞概率和提高CCH的利用效率,基于路侧单元(road side unit,RSU)协助的VANET异步多信道MAC协议[4-7]和基于RSU协助的VANET同步多信道MAC协议[8-9]得到了广泛研究。虽然上述研究在一定程度上缓解了CCH拥塞,减少了节点访问CCH的碰撞概率,但均未对节点访问CCH的碰撞概率进行定量的理论分析与推导。而基于RSU协助的同步多信道MAC协议(an RSU-coordinated synchronous multi-channel MAC scheme,RC-MCMAC)[10]采用IEEE1609.4标准的信道分配方案、固定同步时长的CCH间隔和SCH间隔,CCH间隔被进一步分割为RSU间隔和请求服务(request for service,RFS)间隔,SCH间隔期间允许CCH上的节点进行信道预约,降低了节点访问CCH的碰撞概率,实现了CCH资源的充分利用。为了从理论上分析采用RC-MCMAC协议的节点访问CCH的碰撞概率以及证明其性能的优越性,选取了(a vehicular enhanced multi-channel MAC protocol,VEMMAC)[6]协议作为比较对象,通过建立马尔科夫链模型,分析和计算车辆节点在一个时隙内获得CCH发送安全信息或者RFS帧的碰撞概率,并通过仿真实验证明了采用RC-MCMAC协议的节点可降低访问CCH的碰撞概率。
1 马尔科夫链模型分析
根据文献[11]、[12],运用马尔科夫链模型推算出单一节点在任意时隙内获得CCH发送安全信息或者RFS帧的碰撞概率。在进行马尔科夫链模型分析之前,本文假设:
①在同一网络中的节点可以相互通信。
②网络中有n个固定的竞争节点,网络中的节点可以广播安全信息,也可作为发起预约节点,发送预约信息。
③每个节点成功发送前一个数据帧后立即进行下一个数据帧的发送,即发送队列始终保持饱和状态,且每个数据帧在发送之前必须等待随机的退避时间。
④节点的随机发送概率和信道访问碰撞概率仅考虑一维马尔科夫模型,即假定节点退避阶段是固定的,文中设置退避阶段m=10。
通过以上假设,每个节点在任意时隙内通过竞争的方式获得CCH的访问权的过程可以采用离散时间马尔科夫链模型进行分析,如图1所示。
该模型采用了二维独立随机过程{s(t),b(t)}进行分析,s(t) 表示给定节点的退避阶数为[0,m]的随机过程,b(t) 表示给定节点的退避时间计数器随机过程,Wi表示节点在第i阶退避阶段的竞争窗口退避值,概率p表示一个节点在一个时隙内竞争CCH发生碰撞的概率,p的值是随着退避阶数的改变而改变,因此相对与其他的参数来说,碰撞概率p的值是一个常量。因此,从图1中的马尔科夫链模型可以推算出非空一步转移概率:

图1 马尔科夫链模型的退避窗口大小Fig.1 Markov chain model for the back off window size
(1)
P{0,k|i,0}=(1-p)/W0,k∈(0,W0-1),i∈(0,m),
(2)
P{i,k|i-1,0}=p/Wi,k∈(0,Wi-1),i∈(1,m),
(3)
P{m,k|m,0}=p/Wm,k∈(0,Wm-1)。
(4)
式(1)表示节点每经过一个空闲时隙,进入到下一个时隙的开始时刻,退避计数器的值会自减1。
式(2)表示节点的退避计数器的值已经为0,并完成了一次成功的传输之后,进入下一次传输之前启动退避计数器,其竞争窗口的值在[0,W0-1]随机确定。
式(3)表示节点在第i-1退避阶段访问CCH发生碰撞。因此,退避阶数加1,退避计数器将进入第i退避阶段,新的竞争窗口的值在[0,Wi]的范围内随机的确定。
式(4)表示节点的退避阶段一旦达到第m阶,则接下来的数据包的发送过程将不再增加。
为了方便分析,令:
P{i1,k1|i0,k0}=P{s(t+1)=i1,b(t+1)=k1|s(t)=i0,b(t)=k0}。
(5)
采用bi,k表示马尔科夫链模型的平稳分布,即:
(6)
结合式(6),很容易推断出马尔科夫链模型的解析解,即马尔科夫链模型的状态转移特性:
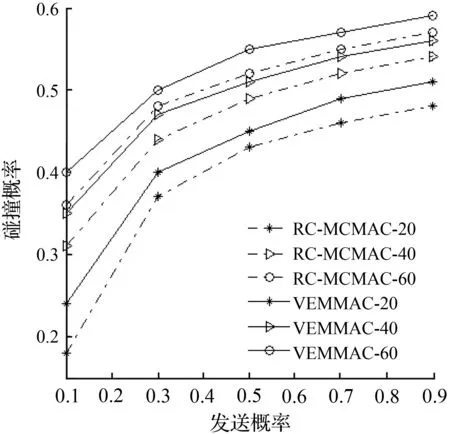
bi-1,0×p=bi,0→bi,0=pi×b0,0, 0 (7) (8) 利用马尔科夫链模型的状态转移特性,当k∈[0,W0-1],则: (9) (10) 通过式(7)、(8)、(10)可以推断出bi,k是变量b0,0和条件碰撞概率p的函数,最后通过对上述模型的平稳分布进行一些必要的化简,并利用一步转移概率矩阵的特性,可以得到: (11) 进一步简化式(11)得到b0,0的最终表达式: (12) 在假设退避阶段m为固定值,且节点的退避计数器的值为0时,那么,节点在任意时隙访问CCH成功发送信息的概率为: (13) 令p表示已经有一个节点在当前时隙内占用了CCH的前提下,此时至少有一个节点访问CCH发生碰撞的概率,那么: p=1-(1-τ)n-1。 (14) 将式(13)、(14)与RC-MCMAC协议相结合,并假设节点在单位同步周期中发送安全信息的概率为sr1,节点在单位同步周期中发送预约信息的概率为sr2,那么,在n个节点的网络中,单位同步周期中发送安全信息的节点数为N1=n×sr1,发送预约信息的节点数为N2=n×sr2,N2个发起预约的节点在RFS间隔和SCH间隔访问CCH的的过程遵循二项分布,即每个节点选择RFS间隔和SCH间隔的概率均为1/2,因而平均分布到RFS间隔和SCH间隔的节点个数为N2/2。另外,RC-MCMAC协议只允许安全信息在RFS间隔发送。因此,在RFS间隔竞争CCH的节点个数为(N1+N2)/2,在SCH间隔竞争CCH的节点个数为N2/2,设τrτr为节点在RFS间隔任意时隙成功访问CCH的概率,τs为节点在SCH间隔任意时隙成功访问CCH的概率,pr为节点在RFS间隔访问CCH的碰撞概率,ps为节点在SCH间隔访问CCH的碰撞概率,由式(13)、(14)推算出τr、pr及ps: (15) (16) pr=1-(1-τr)N1+(N2/2)-1, (17) ps=1-(1-τs)(N2/2)-1。 (18) 综上可知,利用式(17),(18)可以分别计算出采用RC-MCMAC协议的节点在RFS间隔和SCH间隔访问CCH的碰撞概率。下面将通过一系列仿真实验来验证节点访问CCH的碰撞概率分析模型。 为分析上述马尔科夫链模型得出的节点访问CCH的碰撞概率,同时,凸显RC-MCMAC协议在同步多信道MAC协议方面的性能优势,仿真实验比较了RC-MCMAC协议和VEMMAC协议在节点访问CCH上发送信息的碰撞概率,实验设置了安全信息的发送概率与预约信息的发送概率相同,即s=sr1=sr2,理论模型仿真参数如表1所示。 表1 理论模型仿真参数Tab.1 System parameters for simulations 图2给出了RC-MCMAC协议在不同的发送概率下的碰撞概率随节点数变化曲线,此结果一方面验证了节点访问CCH的碰撞概率随着节点数的递增而不断增加。另一方面也说明了在同一发送概率的情况下,网络内节点数越多,节点访问CCH的碰撞概率就越大。所以,有必要采取措施降低同一时间段内访问CCH的碰撞概率。 图2 RC-MCMAC协议在不同的发送概率下的碰撞概率随节点数变化Fig.2 Collision probability of RC-MCMAC under different transmission probability 图3给出了RC-MCMAC协议和VEMMAC协议的碰撞概率随节点数变化曲线。当发送概率由0.1增加到0.5时,随着节点数的增加,RC-MCMAC协议和VEMMAC协议的碰撞概率也随之增加。但是,VEMMAC协议的碰撞概率增加的更多,其主要原因是该协议只允许节点在CCH间隔进行安全信息的广播、业务信道预约信息和其他类型业务的传输,短暂的CCH间隔不能很好地满足节点的密集访问,导致信道拥塞和访问冲突;而RC-MCMAC协议允许节点在RFS间隔和SCH间隔都可以访问CCH,不仅降低了碰撞概率,而且提高了CCH利用率。该结果说明,给CCH划分多个访问间隔也是一个减少碰撞概率的方法。 图4给出了RC-MCMAC协议和VEMMAC协议的碰撞概率随发送概率变化曲线。该曲线说明了随着节点的发送概率增加,节点数由20增加到60时,节点访问CCH的次数也增多,导致节点访问CCH的碰撞概率不断上升。当发送概率和节点数持续增加,碰撞概率也随着增加。但RC-MCMAC协议的碰撞概率明显低于VEMMAC协议,说明RC-MCMAC协议将CCH间隔分割为RSU间隔和RFS间隔,SCH间隔期间允许CCH上的节点进行信道预约,降低了碰撞概率,同时,仿真结果也表明了在节点数增加时,应尽量减少节点发送信息的概率,进而减少碰撞的发生。 图4 RC-MCMAC协议和VEMMAC协议的碰撞概率随发送概率变化Fig.4 Collision probability of RC-MCMAC and VEMMAC under different transmission probability 本文通过建立离散马尔科夫链模型,分析了采用RC-MCMAC协议的节点访问CCH的碰撞概率,并通过仿真对比实验证明了RC-MCMAC协议具备更低的碰撞概率,且优于当前同类别的VEMMAC协议,其主要得益于RC-MCMAC协议将CCH间隔进一步分割为RSU间隔和RFS间隔,允许CCH上的节点在SCH间隔进行信道预约,不但实现了CCH资源的充分利用,而且降低了节点访问CCH的碰撞概率,对提高安全信息的高可靠发送至关重要。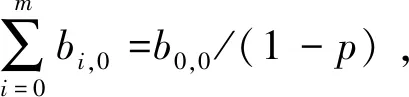
2 理论模型结果分析


3 结论
