瑕疵谐振石英半球壳固有刚性轴的定位

谭品恒，周闯，邓文高，张家欧

(广西大学机械工程学院， 广西南宁530004)

0 引言

随着对航空航天领域研究的深入，高精度惯性导航定位成为此领域日益重要和备受关注的研究课题[1-4]。近几十年来，航空航天陀螺仪也历经几代变换升级。其中，半球谐振陀螺仪以其高精度、高可靠性以及寿命长等特点成为陀螺仪里最具发展前景的一种[5-8]。但也是因为这种特性，使这种陀螺仪中核心结构的石英半球壳(如图1所示)的制造工艺要求十分精细。在石英半球壳制造工艺过程中难免产生微观的孔隙与晶相结构变异，造成宏观的密度和阻尼不均匀等瑕疵[9-11]，这对半球谐振陀螺仪的高精度工作性能有着极大的影响[12-13]。

图1 半球谐振陀螺仪的结构
Fig.1 Structure of Hemispherical Resonator gyroscope

半球谐振陀螺仪是惯性导航元件中对于物体姿态测量的模块，其主要通过二阶模态的振动形成驻波，当基座随物体旋转时，由于科氏力的作用，驻波会相对基座产生进动，其中驻波相对激发振动的进动角度与基座自身旋转的角度有恒定的比例关系，如公式(1)：

θ=Kφ,

(1)

其中θ为驻波进动角度；K为比例因子；φ为基座旋转角度。通过感测电极解算测得驻波进动角度θ，根据上式可得到基座旋转角度，即物体旋转角度[14]。

无瑕疵的理想状态半球壳，其激发模态与感测模态的固有频率是相同的，然而密度和阻尼瑕疵会使此两频率分歧(即所谓的频率裂解)，并导致测量的角速度有一些误差，从而严重影响半球谐振陀螺仪的工作精度。李巍等[15]也尝试设计过测试固有刚性轴的方案，但其理论和操作相对复杂，而且缺乏实验或者仿真支撑。根据目前相关文献[16]可知，当半球谐振陀螺仪同时存在密度和阻尼瑕疵时，可以在低频固有刚性轴的所在方位的半球壳唇缘蚀刻去一定的质量，半球壳的固有刚性轴在此蚀刻过程中方位不会发生变化，以此方法达到减少频率裂解的目的。本方法建立在这个基础上，通过强迫振动测试和李萨如图观察，能较快较准确地定位固有刚性轴。

1 固有轴系的定义

1.1 固有刚性轴

图2 固有刚性轴Fig.2 Normal mode axes

半球谐振陀螺仪的误差主要来源于谐振子的材料、工艺缺陷。其中对谐振子工作驻波影响最大的是密度ρ、杨氏模量E、薄壳的壁厚h等参数的不均匀性的傅里叶展开式的第四次谐波。该谐波的存在导致谐振子中出现2个成45°的固有轴系。如图2所示，谐振子沿每个轴振动的固有频率都能达到极大值和极小值。其频率极大值和极小值的差称为固有频率分裂：Δω=ω2-ω1，其中ω1、ω2为固有频率。固有频率小的刚性轴即A-A轴(ω1)称为“重”轴，也称为小刚度轴；固有频率大的刚性轴B-B轴(ω2)称为“轻”轴，也称为大刚度轴[14]。若将x和y振幅的运动方程式转换到固有刚性轴上，则运动方程式会变为非耦合形式。这样修正某一轴的频率，不会影响到另一轴的频率。

1.2 固有黏性轴

半球谐振子在有阻尼的情况下存在能量耗散使振幅衰减，如果谐振子的品质因数沿半球壳圆周角分布不均匀，即阻尼分布不均匀(阻尼瑕疵)，就使驻波发生偏移。由于缺陷四次谐波的存在，使得谐振子中出现2个成45°的轴系，称为“固有黏性轴”(principal damping axes)。谐振子振动的时间常数τ2和τ1沿着2个轴的每一个轴方向将达到极大值和极小值。由材料品质因数不均匀(阻尼分布不均匀)造成的漂移速度一般难于进行机械补偿，通常通过算法来补偿[14]；这主要是因为品质因数与很多因素有关，如喷镀导电层、残留的气体压力、空气微粒落入表面等都将造成品质因数的变化。由于瑕疵的随机性，固有刚性轴和固有黏性轴一般不会重合。

2 强迫振动稳态时半球谐振子运动呈封闭椭圆状的证明

2.1 基于笛卡尔坐标系下解析方程式证明

根据二维弹簧—阻尼—质点运动物理模型，参考图3，本文用Lynch的方法[16]表示半球谐振子在笛卡尔坐标系下的运动方程(2)，其中x轴代表激励电极所在方向，x代表此方向的质点位移；y轴代表感测电极所在方向，y代表此方向的质点位移。激励电极与感测电极在实际半球壳上始终保持相隔45°摆放，而在此模型笛卡尔坐标系x-y中，它们分别代表x和y并且始终保持相隔90°，于是在此坐标系下的角度始终为实际半球壳上角度的两倍。

图3 谐振半球壳二维弹簧—阻尼—质点运动物理模型Fig.3 Two dimension spring-damping-particle kinetic physical model of hemispherical resonant shell

(2)

式中

(3)

ω1：极小值固有频率；ω2：极大值固有频率；Δω：固有频率裂解值；τ1：极小值阻尼时间常数；τ2：极大值阻尼时间常数；θω：固有刚性轴与x轴夹角；θτ：固有黏性轴与x轴夹角；θf：施力方向与x轴夹角。

在强迫振动测试定位时，半球壳是固定不动的，所以Ω=0；激励电极位于半球壳直径的两端处，激励电极输入的是一对余弦力，所以fx=Acosωt,fy=0，将式(2)重写为下列形式：

(4)

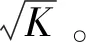
其稳态时解的形式为：

x=Rcosωt+Ssinωty=Pcosωt+Qsinωt,

(5)

其中R、S、P、Q为常数。

将式(5)代入方程(4)有方程组(6)如下：

-A+K12P+K11R+ω(D12Q+D11S-Rω)=0K12Q+K11S-ω(D12P+D11R+Sω)=0K22P+K12R+ω(D22Q+D12S-Pω)=0K22Q+K12S-ω(D22P+D12R+Qω)=0,

(6)

(7)

(8)

(9)

(10)

本文将式(5)改写成矩阵形式，有：

(11)

进一步得：

(12)

令Δ=RQ-PS,本文可以得到：

(13)

(14)

根据二次曲线的判别式来讨论方程(14)是表示椭圆、双曲线还是抛物线。已知一般的二元二次曲线方程为：

ax2+2bxy+cy2+2dx+2ey+f=0，

(15)

(16)

(17)

根据判别式条件有：①当I3=0时，方程为直线；②当I3≠0时，1.I2>0时方程为椭圆；2.I2<0时方程为双曲线；③I2=0时方程为抛物线。则具体到已知方程式有：

(18)

(19)

(20)

f=-1。

(21)

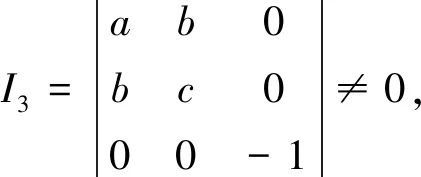
b2-ac<0，

(22)

进一步有：

(23)

(24)

若要满足式(24)，只要Δ=RQ-PS≠0即可。而在实际情况中，根据R、Q、P、S的解析式可知RQ≠PS是成立的，这便从解析上证明强迫振动最终稳态时，质点运动曲线为一封闭的椭圆。

2.2 基于Mathematica李萨如图的数值仿真

通过图4和图5可以明显看出在强迫振动稳态下半球谐振子运动的李萨如图一般情况为一个封闭的椭圆，这从仿真上验证了理论解析证明的正确性。

3 含瑕疵半球壳固有刚性轴的定位

3.1 强迫振动稳态时椭圆参数的解析形式

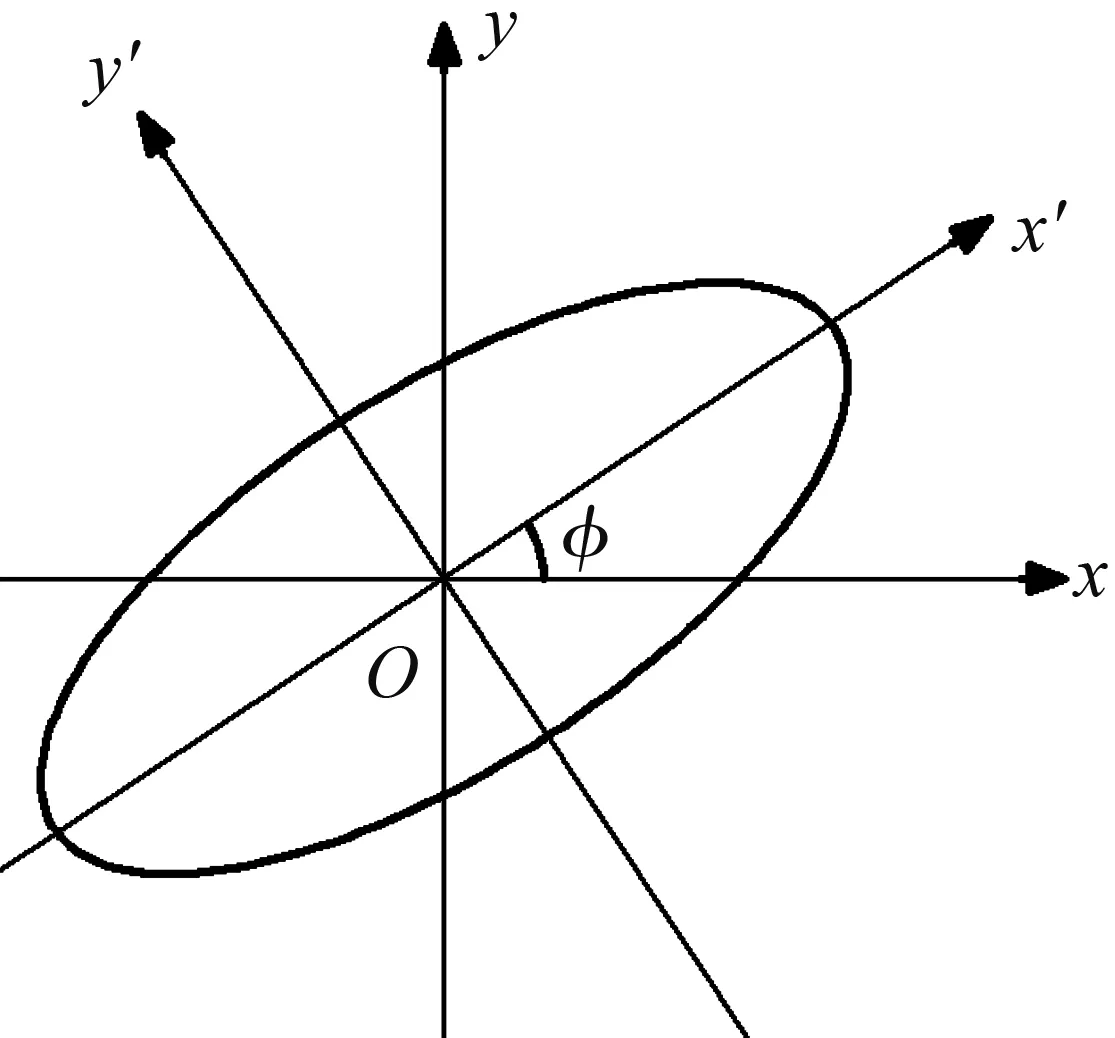
图6 椭圆方程的坐标变换Fig.6 Coordinate transformation of elliptic equation

根据已知的方程可知，方程所代表的椭圆与坐标轴x-y有一倾角φ，而当进行坐标变换时，可以通过将原坐标旋转φ角使椭圆的两主轴与新的坐标轴x′-y′分别平行。求出此φ角便可确定稳态时椭圆倾角。

如图6所示，当坐标轴从x-y旋转φ到坐标轴x′-y′后，坐标之间的变换满足下式：

(25)

则原坐标用新坐标表示为：

(26)

将(26)式代入(14)式有：

(27)

经过坐标变换后得到的新坐标轴下表示的椭圆方程为式(27)，若要满足椭圆主轴与新坐标轴分别平行，则应满足x′y′项的系数为“0”：

(28)

通过式(28)可以求得坐标轴的旋转角度φ：

(29)

同时椭圆的长半轴a和短半轴b也可以得出：

(30)

(31)

3.2 数值仿真与分析

坐标变换旋转的角度φ决定了稳态时椭圆的倾角。而由于R、Q、P、S表达式的复杂性，椭圆倾角φ也不能通过直接求解其导数而得到最小值。因此，利用李萨如图数值仿真模拟的方式同时配合φ相对于θf的函数图像对其进行研究。

本文模拟一般情况的谐振半球壳，给定预设的初始条件:正弦力振幅A=0.01 N，ω1=5 200 Hz，ω2=5 200.01 Hz，τ1=300 s，τ2=440 s，θω=30°，θτ=-10°。改变激发角度θf，观察谐振半球壳稳态时运动的李萨如图(图7～图14)。

图7 激发角θf=30°李萨如图
Fig.7 Excitation angleθf=30° Lissajous-Figure

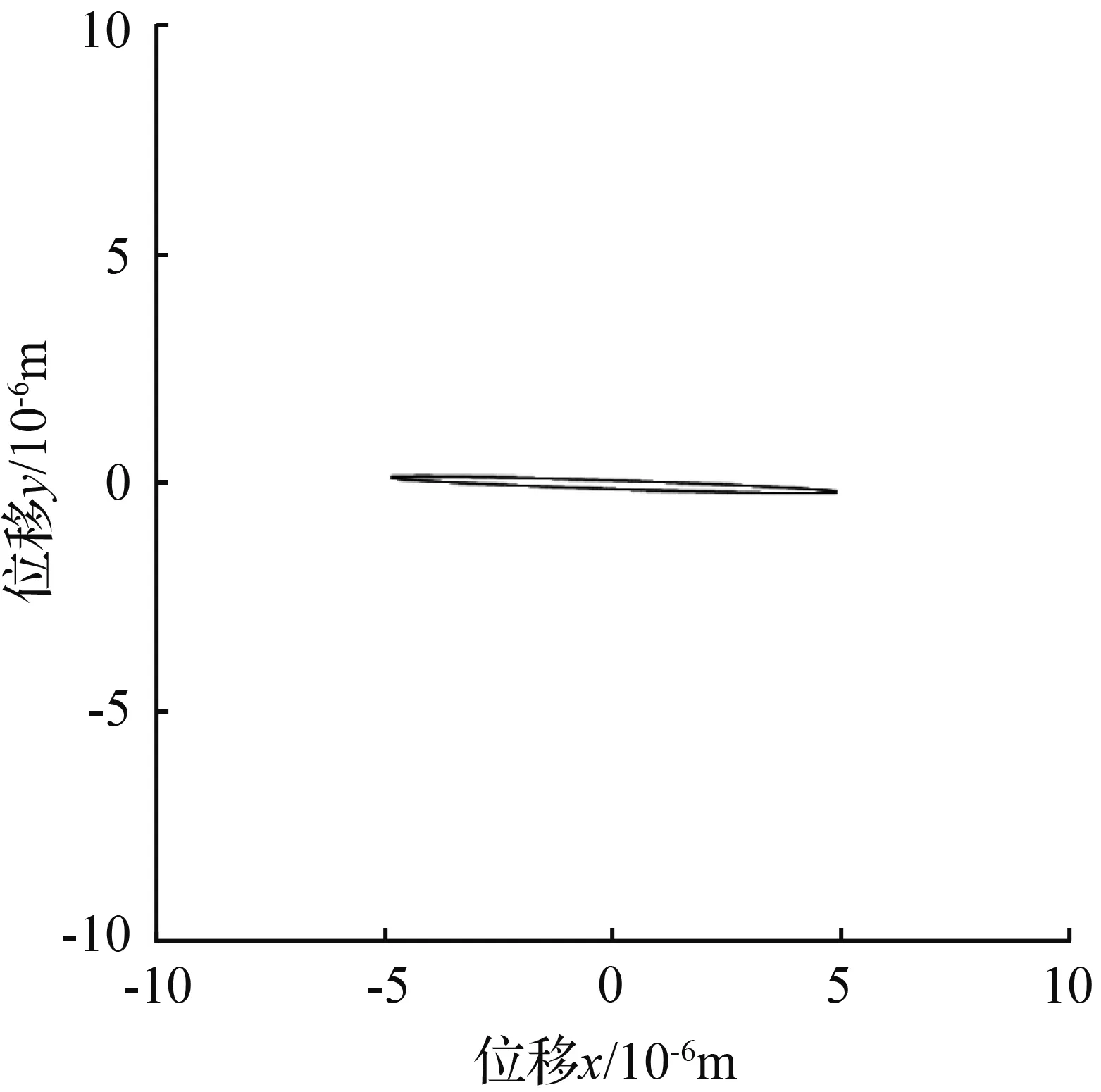
图8 激发角θf=31°李萨如图
Fig.8 Excitation angleθf=31° Lissajous-Figure

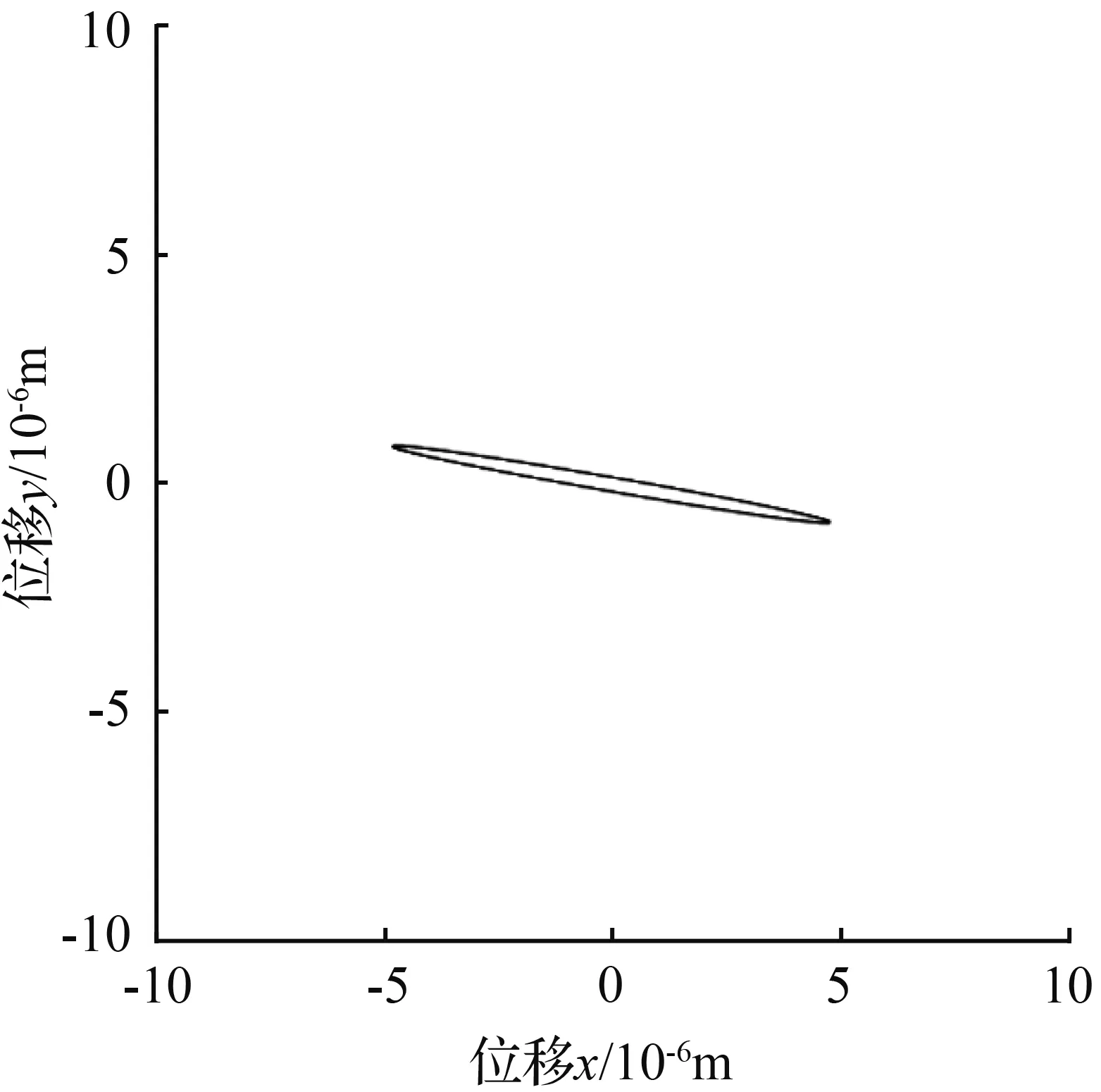
图9 激发角θf=35°李萨如图
Fig.9 Excitation angleθf=35° Lissajous-Figure

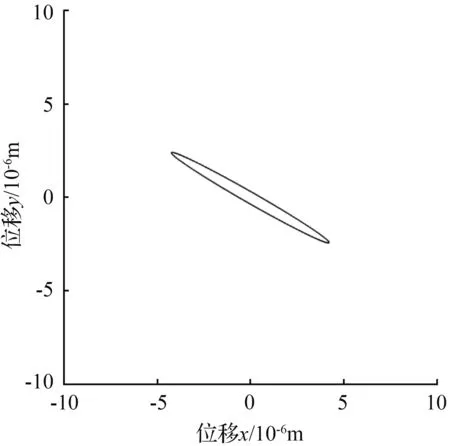
图10 激发角θf=45°李萨如图
Fig.10 Excitation angleθf=45° Lissajous-Figure

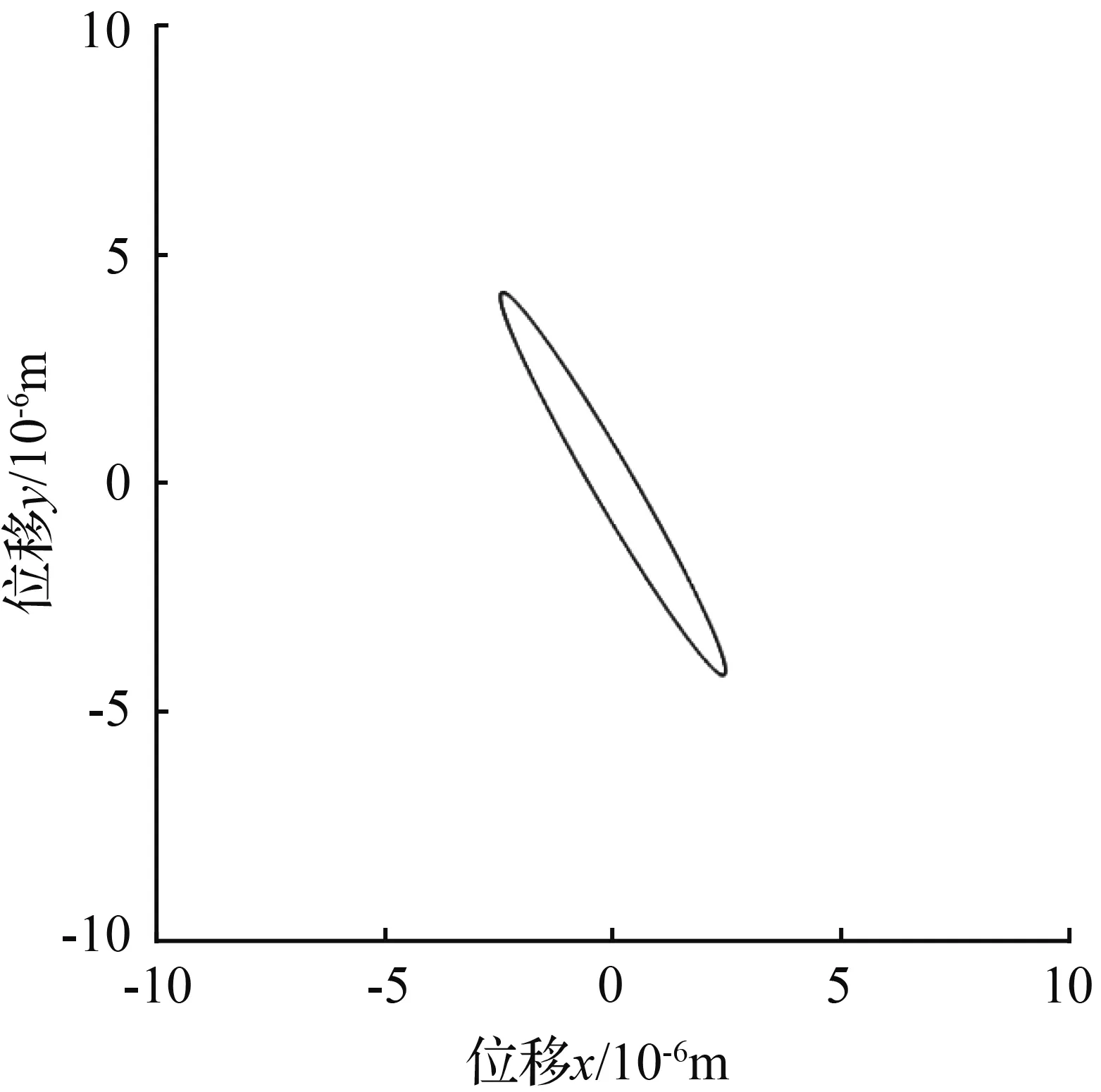
图11 激发角θf=60°李萨如图
Fig.11 Excitation angleθf=60° Lissajous-Figure

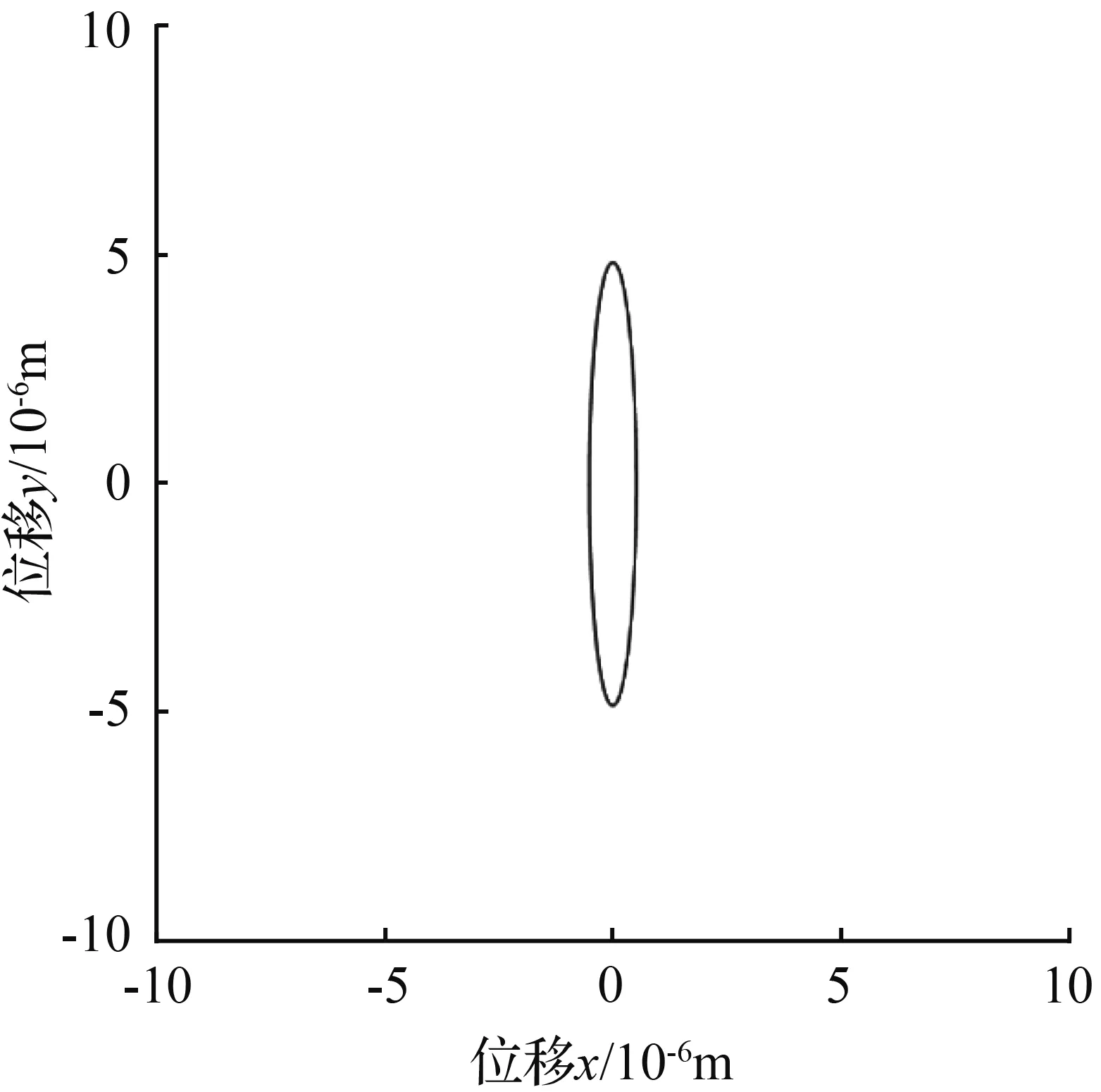
图12 激发角θf=75°李萨如图
Fig.12 Excitation angleθf=75°Lissajous-Figure

图13 激发角θf=90°李萨如图
Fig.13 Excitation angleθf=90° Lissajous-Figure

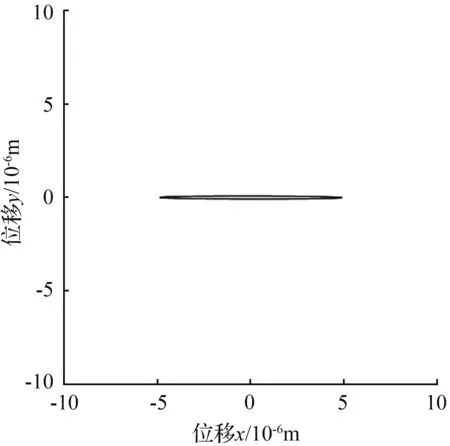
图14 激发角θf=120°李萨如图
Fig.14 Excitation angleθf=120° Lissajous-Figure

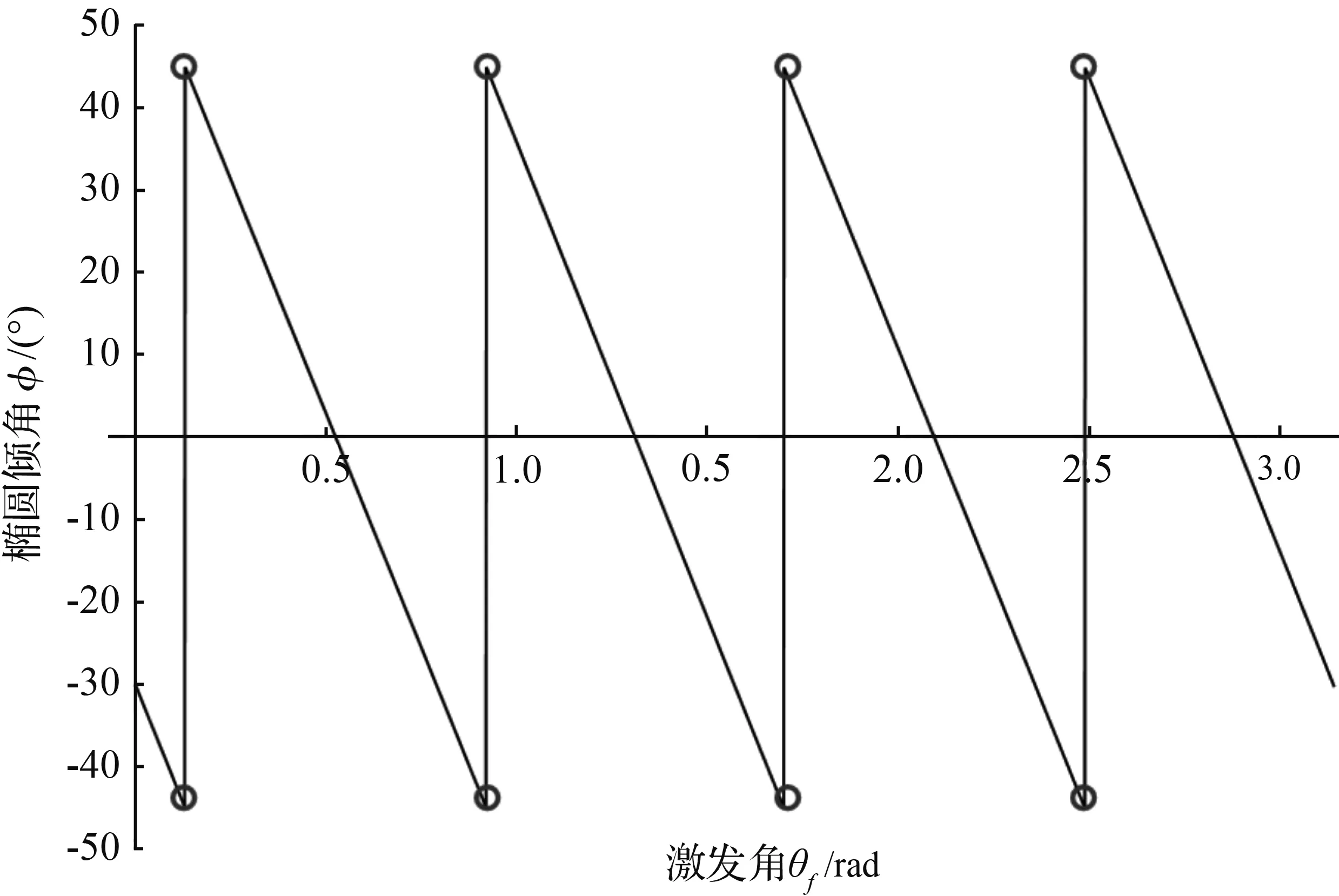
图15 稳态时椭圆倾角φ随激发角θf的变化Fig.15 Change of elliptic inclination φ with excitation angle θf at steady state

从图7到图14可以看出，随着激发角θf从30°变化到120°，稳态时李萨如图的椭圆倾角φ从0°变化到180°。基于给定的初始条件θω=30°，而另一固有刚性轴在李萨如图中为120°(实际球壳中两固有刚性轴应相差45°)，由此可以判定在固有刚性轴上进行强迫振动激发，得到的稳态李萨如图椭圆呈水平状态，倾角φ为零，即与x轴重合。图15描述的是式(29)的图像，它直观的表现了激发角在0～π弧度之间时，稳态椭圆倾角φ的变化。经Mathematica计算，在0～π弧度之间，倾角φ为零时激发角θf的值分别为0.524 32、1.308 84、2.093 63、2.879 90，分别对应30.041 1°、74.991 1°、119.756°、165.006°。其中需要注意的是75°和165°对应的是图12所示的情况，而由于倾角函数φ(29)的周期为π/2，所以当倾角φ值超过-45°后便以此倾角的补角方向来计算，这也解释了图15中从0.524 32到1.308 84这一段图像中间倾角φ值为什么从-45°跳变到45°。另外，正是由于倾角函数φ(29)是由tan函数反推得来，所以倾角φ取不到45°或者-45°处的值，在图15中圆圈所标识出的点以及两点间整条直线是无法取到的，则在此点所在横坐标处应为断点。于是倾角φ为0°(或180°)对应的激发角θf分别为30.041 1°(119.756°)。

综上可知，在含有耦合瑕疵谐振半球壳固有刚性轴所在的方位的进行激发的强迫振动稳态椭圆的倾角一定是为0°(椭圆是水平的)。故可以通过以上现象归纳的方法去测试一个未知具体参数的含耦合瑕疵谐振半球壳的固有刚性轴的具体方位角：给定一个半球壳任意直径两端处一个余弦力，使其保持强迫振动，待振动稳定后观测x和y两处感测电极的位移李萨如图，若呈现一封闭的倾角与x轴重合的椭圆，则可定位此激发处为固有刚性轴所在方位。否则，再更换另外的角度进行强迫振动激发，直至出现上述李萨如图，便可定位其固有刚性轴。

4 结论

本研究针对的半球谐振陀螺仪是同时含有密度瑕疵和阻尼瑕疵的，这是实际中所知的半球谐振陀螺仪的一般情况。通过Lynch的二维弹簧—阻尼质点运动模型建立的方程，在半球壳直径两端施加一对方向相反的余弦力以达成强迫振动。为了使观察到稳态时的李萨如图更有说服力，本文证明了强迫振动稳态时李萨如图为一封闭的椭圆，这也为后续观察椭圆倾角提供了可能。当给定了初始条件和半球壳特性参数后，得到了强迫振动稳态时李萨如图的椭圆倾角与激发角度的关系，并提供了相应的李萨如图。仿真实验表明，若以固有刚性轴方位角作为激发角来完成强迫振动，则稳态时李萨如图的椭圆一定与x轴是重合的，即椭圆的倾角与激励电极所在的x轴相差最小。通过这一现象，可以给未知具体参数的含耦合瑕疵的半球谐振陀螺仪进行固有刚性轴的定位。