垂直/倾斜型交错狭缝光栅对立体显示效果的影响

陈 瑜，赵 焱，曾祥耀，姚剑敏，叶 芸，林志贤，陈恩果

(平板显示技术国家地方联合工程实验室,福州大学 物理与信息工程学院，福州，350116)

1 引 言

自由立体显示器由于无需佩戴立体眼镜等辅助设备、结构简单、成本低廉和显示效果好等优点，已成为立体显示研究的热点[1]。利用传统垂直狭缝光栅实现自由立体显示的方法，存在着一些明显的缺陷。比如不同视点的图像间会发生相互串扰[2]，可视区域变小[3]，存在莫尔条纹现象等[4]。莫尔条纹是由于光栅的狭缝与液晶显示器的列像素平行排列，当人眼通过狭缝看到相邻子像素之间的黑矩阵时，产生明显的周期性黑白渐变条纹。针对立体显示的串扰问题和莫尔条纹现象方面，Liang 等使用遗传算法来优化改善柱透镜参数来降低串扰[5]； Hanhart等通过优化系统输出视图、执行智能动态分配以最小化串扰[6]；Zhuang等提出了一种确定双凸透镜薄膜的优选倾斜角度的方法，使准立体显示器中的莫尔条纹最小化[7]。因此，如何提高狭缝光栅自由立体显示器的立体显示效果成为众多高校和研究机构的研究热点。

交错式光栅设计方案能够增加可视区域的大小，而对莫尔条纹影响较小，兼顾了可视区域和莫尔条纹之间的平衡关系[8]。本文从狭缝光栅的立体显示原理出发，理论分析狭缝光栅的倾斜角度、狭缝宽度、狭缝错开距离对立体显示效果的影响，优化了倾斜交错狭缝光栅和垂直交错狭缝光栅两种立体显示器件，实验对比了两种器件的立体显示效果。

2 狭缝光栅立体显示原理及光栅参数的影响

2.1 狭缝光栅自由立体显示原理

人类双眼能够感知不同物体的距离是由于左右眼的视差特性，使得人眼可以根据看到的画面判定物体的深度，确定物体的立体特性。图1(a)所示为双目视觉模型。人眼两瞳孔之间存在着大致 60～70 mm的间距，这样使得人的双眼会从稍有不同的两个角度去观察物体，由于几何光学投影，左右眼视网膜的成像存在着细微的差别，这就是双目视差。双目视差能反映场景中物体的深度信息，人类大脑皮层对存在视差的左右眼图像进行融合后，便能提取信息并感受到具有层次感的立体视效。

如图1(b)所示，实际场景中的点P在人左右视网膜上的成像点分别为Pleft、Pright，焦距为f，OL和OR是左右眼睛成像中心，左右眼成像中心之间距离的用BL表示。左右眼睛在同一平面上，因此他们的投影中心的y轴坐标相等。同一时刻空间点P(x,y,z)在两相机上成像点分别为Pleft和Pright。根据三角关系可得：

(1)

(a)双目视觉模型(a) Binocular vision model

(b)双目成像原理图(b) Schematic diagram of binocular vision imaging图1 双目视觉原理图Fig.1 Schematic diagram of binocular vision

设视差为D=Xleft-Xright,引入参数视差D后可得出特征点P在人眼坐标系下的三维坐标为：

(2)

由此人眼可以拟合出物体P点的三维信息，场景中物体的立体效果就被人所接收。

图2 狭缝光栅显示原理图Fig.2 Slit grating display principle diagram

狭缝光栅自由立体显示的原理正是利用了人眼视差特性进行设计的，显示原理如图2所示，狭缝光栅位于显示器前方，与液晶显示器精密耦合而成。观察者左(右)眼透过光栅上的狭缝只能看到显示器上的奇(偶)像素列。其实现立体显示的原理如图1所示。在图2中，一般说来，两眼之间的距离BL的取值为65 mm，并假定狭缝透光宽度为a，狭缝光栅的黑条宽度为b，液晶显示器的子像素宽度为c，狭缝光栅与液晶屏的距离为d，最佳观看距离为L。而L的取值由显示器制备者根据显示器摆放的环境不同而各有不同。在本文中，L取值为210～220 cm。

2.2 狭缝光栅参数条件的影响

2.2.1 光栅倾斜角度对莫尔条纹和分辨率的影响

为了防止背景光泄露，提高显示对比度，防止液晶混色，在2D液晶屏的子像素之间加入不透光的周期性黑矩阵，形成像素阵列。黑矩阵与光栅狭缝产生一系列交叉点，无论横向、纵向或斜向都会形成不同方向的条纹，即莫尔条纹。莫尔条纹是两条线或两个物体之间以恒定的角度和频率发生干涉的视觉现象，人眼无法分辨这两条线或两个物体，只能看到干涉的花纹，如图3所示。通过沿不同方向连接交叉点，得到不同方向莫尔条纹的宽度为W[9]

(3)

n为正整数，A是子像素宽度，B是狭缝光栅的狭缝宽度(常数)。根据公式(3)可知，当A、B一定时，通过调整光栅与黑矩阵之间的倾角θ，就能减小莫尔条纹的宽度，从而有效减轻莫尔条纹现象[9]。

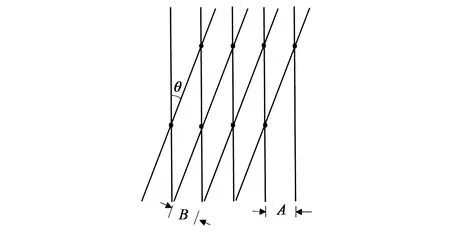
图3 莫尔条纹形成的原理图Fig.3 Moire fringe pattern formation

2.2.2 狭缝宽度对可视区域和串扰的影响

图4 狭缝光栅自由立体显示器的几何模型Fig.4 Geometric model of a slit grating free stereo display

自由立体显示器在播放视点图像时，人眼能在显示器前方观看到视点图像而形成的立体区域称为可视区域，如图3所示。当人眼偏离可视区域之外，双眼接收到的或者是无视差的左右眼图像，或者是左右眼图形的混叠，称之为立体图像串扰。由图4可知，直线D1F1和C2F2的交点与直线B1G1和D2G2的交点横坐标之差u表示水平方向可视区域的大小。当视点数K确定时，狭缝光栅的周期是定值。为了尽可能减小人眼看到串扰的几率，要尽量增大可视区u值，由式(4)可得[11]，可视区域u随着狭缝宽度a的值改变而改变。若减小狭缝宽度a，图像亮度降低，但可视区域u变大，图像串扰值减小。说明减小串扰值，增大可视区域u是以牺牲亮度值为代价。因此，设计狭缝宽度的基本思路是平衡这3个参量的关系，保证显示亮度足够的情况下，适当调整狭缝宽度a的值以降低串扰，增加可视区域u。通常a1为狭缝宽度理论值，与子像素宽度c相同，以24英寸LCD屏为例(分辨率为1 920×1 080，子像素宽度为0.092 2 mm)，此时a1取0.092 2 mm。为保证显示亮度，串扰度CL应小于15%，光损失不大于60%[12]。公式(4)是3个参量之间的关系。

(4)

其中：a为狭缝透光宽度，b是狭缝不透光宽度，c是子像素宽度。

2.2.3 狭缝错开宽度对莫尔条纹亮度的影响

狭缝错开宽度e不同对莫尔条纹亮度和可视区域u会产生不同的影响。对于竖直交错光栅而言，如图5(a)～5(d)所示。液晶屏的黑矩阵宽度f为0.020 0 mm，光栅狭缝宽度a为0.073 8 mm。图5(a)、(b)为光栅狭缝错开宽度e分别为0 mm和0.053 8 mm 的结构图。从图5(a)、5(b)中可知，上下错开的狭缝始终都覆盖黑矩阵边框f的整个宽度，因此光栅狭缝错开宽度e小于0.053 8 mm时，莫尔条纹的可视亮度最低。图5(c)为光栅狭缝错开0.073 8 mm 的结构图。从图5(b)和5(c)可知，狭缝错开宽度从0.053 8 mm 增加到0.073 8 mm时，莫尔条纹的最低可视亮度随着错开宽度的增加而增加。可见图5(c)的莫尔条纹可视亮度要大于图5(b)的莫尔条纹可视亮度。图5(d)为光栅狭缝错开距离大于0.073 8 mm的结构图。考虑到一个子像素的宽度为0.092 2 mm ,当错开距离在0.073 8～0.092 2 mm区间时，由图5(d)可知，光栅狭缝错开距离无论怎样变化，莫尔条纹的最低可视亮度始终是0.073 8 mm，最低可视亮度无变化。因此，合理的错开距离应选择在0.053 8～0.0738 mm 之间。

图5 狭缝错开距离示意图Fig.5 Schematic diagram of slit staggered distance

对倾斜交错光栅而言，两个相邻光栅狭缝错开的距离为e，由三角形公式得[11]

e=h×tanθ，

(5)

其中θ是光栅与竖直方向的夹角。这样倾斜交错光栅的狭缝变为矩形状结构，跟子像素的形状相同，可以很好地区分开各视点的子像素，并且减小串扰。

3 垂直交错和倾斜交错狭缝光栅的设计与实验

3.1 狭缝倾角对莫尔条纹影响的实验

图6 不同光栅倾斜角度产生的莫尔条纹实拍图Fig.6 Test pattern of different tilted angle of moire fringes

本实验采用609.6 mm(24 in)液晶显示器,该2D液晶显示器，具体参数如下：分辨率为1 920×1 080，子像素宽度为0.092 2 mm，高度为0.276 6 mm,黑矩阵宽度为0.020 0 mm，狭缝宽度为0.073 8 mm，黑条宽度为0.221 4 mm，(视点数K为4，光栅与显示屏黑矩阵水平方向的频域信号的频率[13]之比q=0.380 1)，理论和实验证明，光栅倾斜角度θ不同，会产生不同的莫尔条纹。如图6(a)～6(g)为光栅倾角θ分别为2.94°，6.13°，9.56°，12.30°，18.28°，26.37°，44.81°时，用佳能G10相机(有效像素1470万，拍摄最高分辨率4416×3312)拍摄实验样机产生的莫尔条纹。实验发现光栅狭缝与竖直坐标轴夹角θ增加时，莫尔条纹出现周期性变化趋势。当光栅狭缝倾斜2.94°时，产生的莫尔条纹最明显，如图6(a)；θ为6.13°时，莫尔条纹几乎无法识别；θ为9.56°时，莫尔条纹相对明显；θ为12.30°时，莫尔条纹再次无法识别；θ为18.28°时，莫尔条纹又比较明显；θ为26.37°时，莫尔条纹第三次无法识别；θ为44.81°时，出现由子像素发光区域的矩阵结构和光栅重叠而产生的彩色莫尔条纹。整个变化过程发现莫尔条纹随着θ的增大，周期性变化。并且狭缝光栅倾角θ仅在6.13°，12.30°，26.37°3个特定值附近(图6(b) 、6(d) 、6(f))，莫尔条纹才能有效消除。

3.2 狭缝错开距离对莫尔条纹影响的实验

本实验在上述2D液晶屏上分别设计垂直交错和倾斜交错两款狭缝光栅器件。对于垂直交错光栅，狭缝错开距离e应大于黑矩阵的宽度，小于光栅狭缝的宽度，即在狭缝宽度和黑矩阵宽度之差到狭缝宽度之间的距离取值，计算可得该距离取值范围在0.053 7～0.073 7 mm之间。本垂直交错狭缝光栅器件错开距离参数e1选择0.053 7 mm。此外，液晶屏是由像素矩阵组成，每个像素单元分解成RGB三基色的子像素。像素的高和宽尺寸相等，是一个正方形，则一个子像素的宽度是其高度的1/3。狭缝光栅分段的长度应该选择在一定的范围，否则若狭缝太长，则双目视差图像在垂直方向上的过渡区不是平滑的过渡，而显示两幅行交错的图像，严重影响显示屏光亮度的均匀性。以本实验所采用的液晶屏为例，狭缝的高度以像素高度的一半以下比较合适，结合目前制备工艺技术的限制，我们截取狭缝分段高度为像素高度的1/2,即h取0.138 3 mm。因此对于倾斜交错光栅器件，由公式(5)计算可得，错开距离e2为0.030 2 mm(θ为12.30°)。图7(a)、7(b)是垂直交错狭缝和倾斜交错狭缝的结构示意图。

图7 垂直交错和倾斜交错狭缝结构图Fig.7 Structure diagram of vertical staggered slit and slanted staggered slit

莫尔条纹测试方法是将佳能G10相机放在最佳观看位置并固定，测试的图像为左视点和右视点都是全白的图像。分别将垂直交错狭缝光栅和倾斜交错狭缝光栅用UV固化胶贴在玻璃上，曝光固化，玻璃厚度为3 mm，玻璃再粘在液晶显示屏的屏幕表面并对齐，拍摄到的莫尔条纹如图8所示。

图8(a)中光栅倾斜角度θ为0°，是传统的垂直光栅，其莫尔条纹频率为0.02/mm,莫尔条纹十分明显；图8(b)是垂直交错狭缝光栅，莫尔条纹频率为0.2/mm，莫尔条纹隐约可见，条纹边廓相对整齐；图8(c)为倾斜交错狭缝光栅，倾角θ为12.30°，莫尔条纹频率为0.019/mm，莫尔条纹边缘轮廓模糊，比图8(b)中垂直交错狭缝光栅的莫尔条纹淡，几乎看不到莫尔条纹，光亮度均匀性最好。可见，垂直交错及倾斜交错狭缝光栅其莫尔条纹均远远小于传统的垂直光栅的莫尔条纹。这两款光栅的设计参数均达到减小莫尔条纹对立体图像影响的目的。

图8 垂直光栅、垂直交错光栅、倾斜交错光栅莫尔条纹测试图。Fig.8 Test pattern of Moire fringes of vertical grating, vertical staggered grating and slanted staggered grating.

3.3 单个视区串扰值及左右尺寸测试

测试时，将佳能相机放置在视点1位置。测试步骤为：(1)视点1图像显示全白，其它图像显示全黑，记录亮度值LLwb；(2)视点1图像显示全黑，其他图像显示全白，记录亮度值LLbw；(3)全部图像都显示全黑，记录亮度值LLbb。则视点1通道的串扰值C1如式(6)所示：

(6)

同理可求得其他视点通道的串扰值。

从表1可得，垂直光栅的串扰均值CL最小，比倾斜交错光栅小1.57%；垂直交错光栅和倾斜交错光栅串扰均值CL接近；垂直交错光栅略优于倾斜交错光栅。

表1 3种不同结构光栅串扰的测量值(%)

Tab.1 Measurement of crosstalk for three different structures(%)

结构垂直光栅垂直交错光栅倾斜交错光栅1st8.610.210.42nd8.710.110.33rd8.710.810.54th9.19.910.2平均值8.7810.2310.35

单个视点可视区域u测试方法是设置左右视差图像一个视点为全白图像，另一个视点为全黑图像，将佳能相机位于视点1，这时看到全白图像，然后将相机在水平方向上慢慢移动，直到只看到全黑图像，这时相机位于视点2，测量相机移动的水平距离，就是单个视点可视区域u1。考虑到所有视点可视区域相同，所以只需要测量一个视点宽度。表2为3种不同结构光栅的单个视点可视区域u。

表2 三种不同结构光栅的可视区域测量值(cm)

Tab.2 Measurement of grating size of single visual area for three different structures(cm)

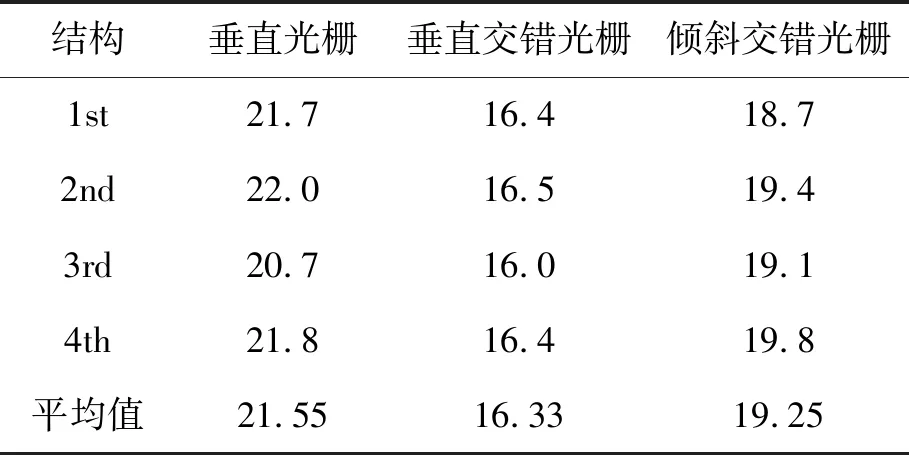
结构垂直光栅垂直交错光栅倾斜交错光栅1st21.716.418.72nd22.016.519.43rd20.716.019.14th21.816.419.8平均值21.5516.3319.25

由表2可知，垂直光栅的单个视点可视区域u最大，均值为21.55 cm，比倾斜交错光栅大2.3 cm；而倾斜交错光栅的单个视点可视区域u与垂直交错光栅相比，大2.92 cm。说明自由立体显示器采用倾斜交错光栅设计可获得远大于采用垂直交错光栅的可视区域，人眼的左右移动范围变大。通过比较垂直交错光栅和倾斜交错光栅，发现两款器件均有效减轻了莫尔条纹，尽管增加了一些串扰，但在串扰仍在15%的范围内。就单个视点可视区域u而言，倾斜交错比垂直交错光栅大2.92 cm，提高了17.9%。再加上倾斜交错光栅所产生的3D图像的分辨率在水平和竖直方向，均有所下降，解决了垂直交错光栅所产生的3D图像分辨率只在水平方向上下降的问题。

从可视区域的实拍图9中可以看出，图9(a)中垂直光栅的黑白过渡区域较小，容易分辨黑白条纹，可视区域最大；图9(b)中垂直交错光栅的黑白过渡区域较大，即串扰区域较大，可视区域较小；图9(c)中倾斜交错光栅的黑白条纹过渡区域较图9(b)的黑白条纹过渡区域而言，倾斜交错光栅的黑白条纹相对更加分明，说明左右眼光线相对集中，即倾斜交错光栅可视区域要好于垂直交错光栅。

综上所述，倾斜交错光栅的3D图像串扰略微大于垂直交错光栅，但是可视区域却有一定程度的增加。

图9 垂直光栅、垂直交错光栅、倾斜交错光栅可视区域实拍图。Fig.9 Test pattern visual area of vertical grating, vertical staggered grating and slanted staggered grating.

3.4 实验样机及左右眼视差实拍效果图

如图10所示为样机3D显示效果实拍图。图10(a)是白底黑字的“1”，图10(b)是黑底白字的“2”，将佳能相机放在显示器前视点观测距离处，从左向右水平移动，在视点1，视点2拍摄的图像。可以看到图10数字边缘轮廓清晰细腻，锯齿状条纹不明显，图像黑白分明，白光显示亮度高，且背景亮度均匀性好，几乎看不到莫尔条纹。说明3D立体显示效果佳。如图10(c)和(d)所示，分别为倾斜型狭缝光栅透过率效果和组装样机显示效果。图10(d)中所示显示屏实拍结果可见，莫尔条纹中暗带的亮度高，在有效减少莫尔条纹的同时又不会引起严重的串扰。

图10 实拍效果图Fig.10 The pictures of actual effect

4 结 论

本文就狭缝光栅的倾斜角度，狭缝宽度，狭缝错开距离等光栅参数对莫尔条纹，串扰，可视区域的影响展开研究。通过理论和实验证明，在控制串扰在允许范围15%内的同时，设计的垂直交错光栅和倾斜交错光栅均能够有效减少莫尔条纹，提出要兼顾可视区域和莫尔条纹之间平衡、光损失匹配的设计理念。优化设计的倾斜交错光栅比垂直交错光栅的可视区域更大，提高了17.9%，并解决了水平和竖直方向上光损失率不匹配的问题，获得亮度均匀性更好的立体显示效果。通过实验样机的拍摄图片证明该光栅器件设计方法的有效性和实用价值。