弹性地基梁法在岩基水闸底板内力计算中的应用
2019-08-27倪成
倪 成
(广州市水务规划勘测设计研究院,广东 广州 510000)
目前土基上的水闸底板分析研究较多,而岩基上水闸底板分析研究较少,主要是应用三维有限元软件(如ABAQUS等)对闸室结构进行整体的分析计算,考虑到中小型水闸项目应用有限元分析计算不实际,根据现行规范,岩基上水闸闸室底板的应力分析可按弹性地基梁法计算[1]。故本文以清远市清新区马安头水电站工程拦河水闸为例,采用弹性地基梁法的文克尔假定,选取不同工况,对岩基水闸底板进行内力计算。
1 工程概况
1.1 水闸情况
马安头水电站总装机1890 kW,正常库容为31.2万m3,总库容为343.6万m3。电站于2004年10月开工建设,于2006年3月建成并投入运行。该电站是清新区滨江河流域开发规划中的第六级电站,已列入清远市江河流域规划,为大流量低水头径流式电站。电能送清远电网,该电站没有调峰任务,为基荷电站。工程属Ⅳ等小(1)型工程,主要水工建筑物为4级,次要建筑物为5级。马安头拦河闸坝采用20年一遇洪水标准设计,50年一遇洪水标准校核。
马安头水电站拦河闸坝主要由拦河陂段、泄洪闸坝段、冲沙闸坝段、消力池组成。本次计算主要复核冲砂闸坝段,冲沙闸闸孔尺寸为1孔8 m×5.0 m,闸底板高29.40 m,闸墩分上、下两级,边墩厚1.6 m,底板厚1 m,顺水流向闸室全长为10.2 m,闸墩、底板采用钢筋混凝土浇筑,采用QPQ2*20 t双吊点卷扬式启闭机,冲砂闸门为平面钢闸门,断面见图1。
1.2 地基情况
马安头水电站水库为河谷型水库,沿河两岸均为低山丘陵,高程在200 m~400 m,山体较雄厚,林木茂盛,植被良好。库区出露的地层主要为燕山期第二期二长花岗岩(ry2)和侏罗系下统(J1)炭质绢云母页岩、炭质石英砂岩、砂砾岩、灰岩等以及第四系冲积、坡积层。其中坝址附近出露的岩石为侏罗系下统(J1)石英砂岩和砂质页岩,其下部为燕山期第二期二长花岗岩(ry2)。
闸坝基础混凝土与基岩接触部位,混凝土与岩石胶结较好。下部基岩为中风化石英砂岩,岩石质量等级为Ⅳ级。实测其天然单轴抗压强度Ra=24.5 MPa~29.7 MPa。根据压水试验成果,该闸坝基岩石透水率5.2 Lu~11.6 Lu,该透水率范围值基本满足规范要求。在勘察深度范围内未发现土洞、空洞、断裂等不良地质现象,也未发现构造断裂踪迹,综合评价场地属稳定场地,地质构造对坝基渗漏的影响甚微。
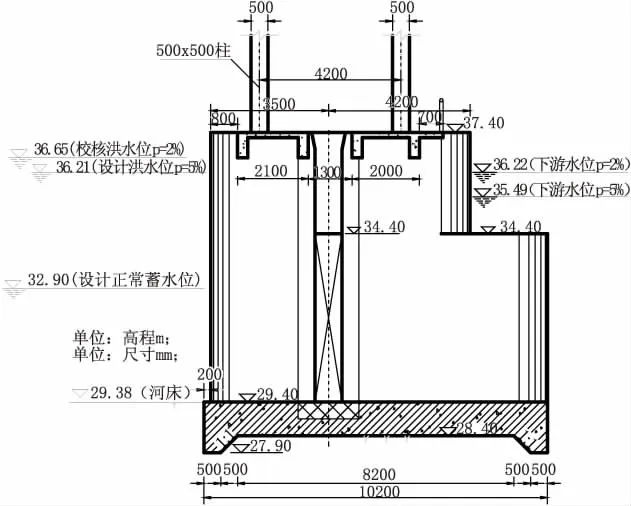
图1 冲砂闸断面图(尺寸单位:mm)
2 底板内力计算
2.1 计算模型
将水闸底板看作弹性地基梁,取单宽底板进行简化模拟计算,长11.2 m,截面宽1 m,高1 m,根据本工程地基情况,基床系数K取500 MN/m3。根据《水工混凝土结构设计规范》(SL191-2008)4.1.7,泊松比取0.17,弹性模量取 25500 MPa。将底板自重、闸内水重、扬压力、分配给底板的不平衡剪力等转换为均布力;将闸墩重力、上部结构传给墩的重力、分配给闸墩的不平衡剪力等转换为集中荷载。参数选择见表1,受力情况见图2。

表1 弹性地基梁法参数选取
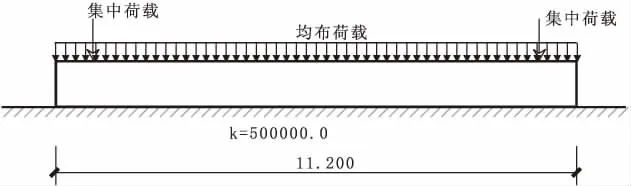
图2 水闸底板荷载计算简图(尺寸单位:m)
2.2 计算工况
对岩基水闸底板的内力分四种工况进行计算,分别为:工况一为完建情况,闸室前后均无水,此时闸基应力最大;工况二为正常蓄水情况,闸前为正常蓄水位32.90 m,闸后取最低水位29.38 m;工况三位设计洪水情况,闸前为设计洪水位36.21 m,闸后取相应水位35.49 m;工况四为校核洪水情况,闸前为校核洪水位36.65 m,闸后取相应水位36.22 m。
2.3 计算不平衡剪力
1)闸底地基反力计算:应力计算公式采用《水闸设计规范》式7.3.4-1:
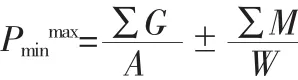
式中:Pminma为闸室基底应力的最大值或最小值;∑G为竖向力之和;∑M为力矩之和;A为闸室基底面积;W为闸室基底面截面矩。
2)不平衡剪力计算:取单位宽度为脱离体,向上的荷载不等于向下的荷载,从而产生不平衡剪力。由于闸门槛上下游段底板上水重不同,以闸门为界,分闸室为上、下游段,各自承担起分段内的上部结构重力和其他荷载,计算不平衡剪力,结果见表2。
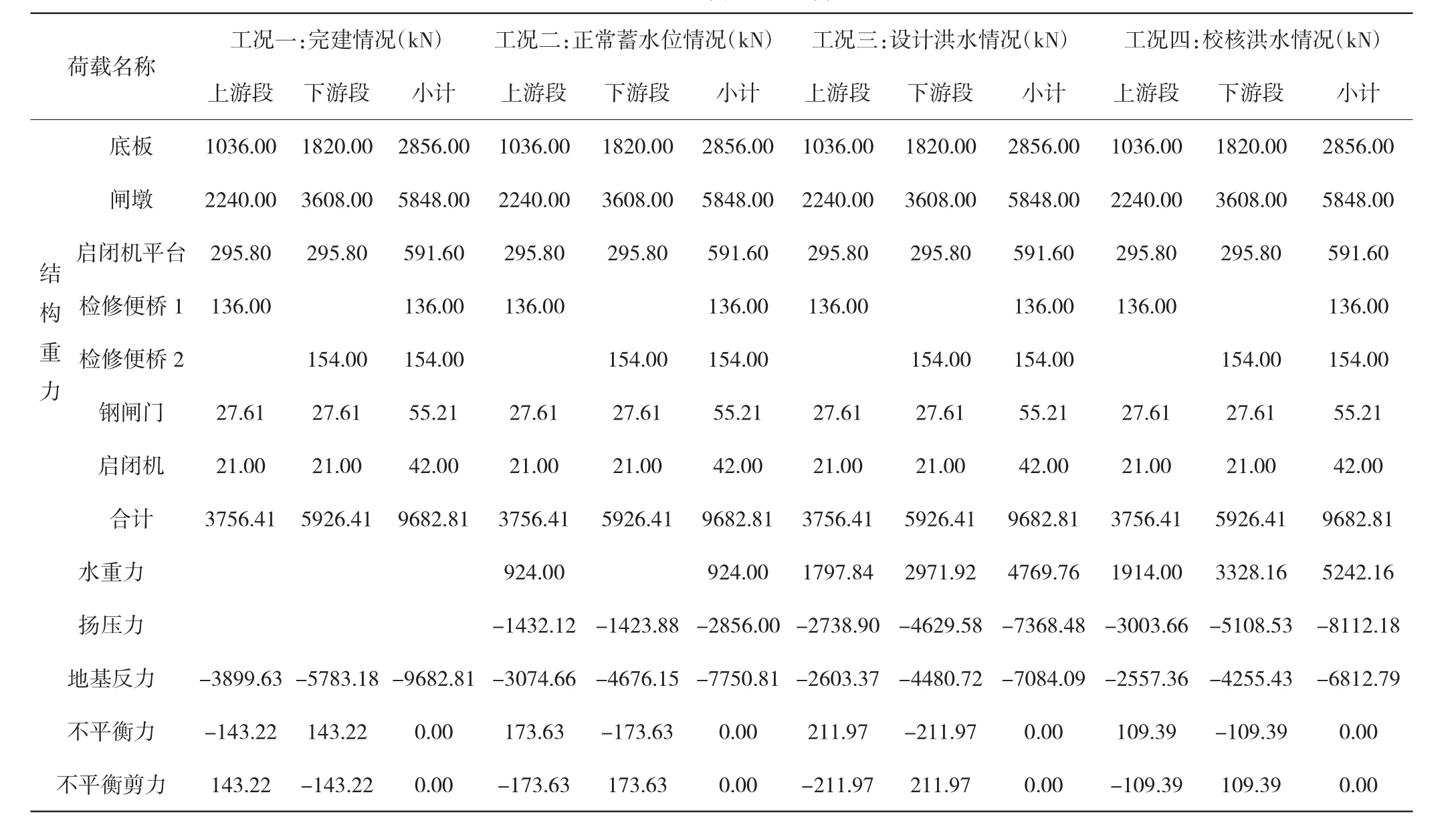
表2 不平衡剪力计算表
由表2可知,四种工况下不平衡剪力均相对较小,在110 kN~210 kN左右,工况三不平衡剪力最大,而工况四最小。究其原因:工况三闸门前后水位差较大,从而导致水闸自重、上下游水重、扬压力、地基反力的合力差值较大,而工况四闸门前后水位差最小,从而导致水闸自重、上下游水重、扬压力、地基反力的合力差值最小。
2.4 计算板条上的荷载
1)分配不平衡剪力
为了在闸墩和底板截面上分配各自的不平衡剪力,可近似按材料力学中矩形截面的剪应力计算公式进行分析[2],如下:
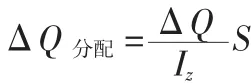
式中:ΔQ为截面上的不平衡剪力;IZ为截面惯性距;S为闸墩和底板分界处静矩。
经计算,底板不平衡剪力分配系数0.23,闸墩不平衡剪力分配系数0.77。
2)板条荷载
将作用荷载分配到单宽底板板条上,计算结果见表3。由表3可知:均布荷载,工况一荷载值最大,工况二下游段荷载值最小,其他工况相差不大;集中荷载,工况一荷载值最大,工况三上游段荷载值最小,工况四下游段荷载值最小。

表3 各工况单宽底板板条荷载情况统计表
2.5 内力计算成果
根据各单宽板条计算荷载,按基床系数法(文克尔假定)计算底板内力,计算成果见表4。
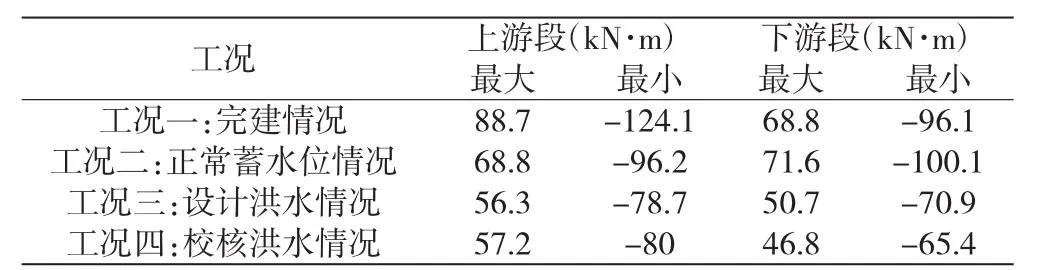
表4 各工况单宽底板板条弯矩计算成果表
由表4可知:上游段控制工况为工况一,最大正弯矩为88.7 kN·m,最大负弯矩为-124.1 kN·m;下游段控制工况为工况二,最大弯矩为71.6 kN·m,最小弯矩为-100.1 kN·m。工况一水闸底板上游段、工况二水闸底板下游段的内力图分别见图3、图4。由于水闸断面是对称的,弯矩的极值也是沿中心对称分布的,极大值位于闸墩中心线处,极小值位于距离梁端约0.26 L(弹性地基梁跨长)处。
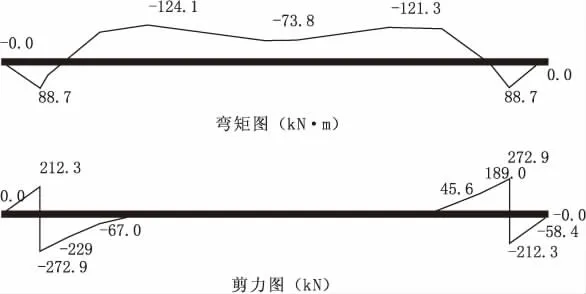
图3 完建工况上游段内力图
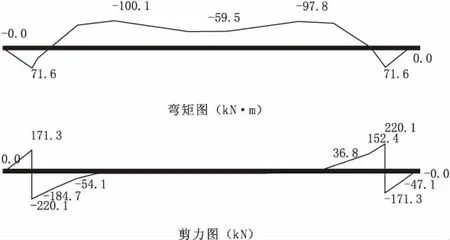
图4 正常蓄水工况下游段内力图
3 结论
本文以清远市清新区马安头水电站工程拦河水闸为例,采用弹性地基梁法,选取不同工况,对岩基水闸底板进行内力计算,提出应用弹性地基梁法计算岩基水闸底板内力,计算结果满足规范要求,符合工程的实际情况,计算过程方便快捷,可对其他类似工程底板计算有一定参考意义。
