基于希尔伯特空间和层次分析法的大坝安全评价模型研究
2019-08-27邢精连
侯 丽,邢精连,周 健
(南京市水利规划设计院股份有限公司,江苏 南京 210001)
0 引言
我国是世界上水能资源最丰富的国家之一,其蕴藏量和开发量均居世界首位。根据2012年第一次全国水利普查结果,我国共有水库9.8万余座,总库容9823.12亿m3,共修建水电站4.67万余座,装机容量达3.33亿kW[1]。水库大坝的安全运行决定了工程综合效益的大小,也间接决定了工程涉及到的国民经济及生命财产的安全。因而进行水库大坝工程的安全监测和评价非常有必要[2]。
水库大坝运行工况复杂,影响条件很多。一般大坝评价模型只基于一般数学统计分析模型进行数据分析,包括原型观测资料正分析、反演分析、反馈分析及大坝安全综合评价专家系统。四类数据分析中原型观测资料正分析评价大坝安全应用较多。其中正分析中的监控模型一般有统计模型、确定性模型、混合模型及其他数学理论建立的模型[2]。一般的数学安全评价模型考虑更多的是数据分析,没有较好地考虑到数据之间的关联性和重要性不同的情况,导致分析结果不是很准确。本文应用层次分析法并结合多维的希尔伯特指标空间构建大坝安全评价模型,对安全指标进行分析,并对各个指标的安全影响因子进行计算。
1 希尔伯特多维指标空间的建立
综合分析大坝安全运行的影响因子,将因子按大坝结构不同分类,根据不同的影响因子建立希尔伯特空间。利用层次分析法确定指标因子的权重并计算出权重算子,最后确立标准的希尔伯特指标子空间。
1.1 评价模型的多层次结构构建
层次分析法的层次结构一般因不同的评价对象而不同。一般分为顶层、中层和底层;其中顶层为最终评价目标层,中层为准则层,中层以下根据评价项目的复杂程度分为层数不同的措施层[3]。其中措施层采用一层的一般评价层次结构,结构图见图1。
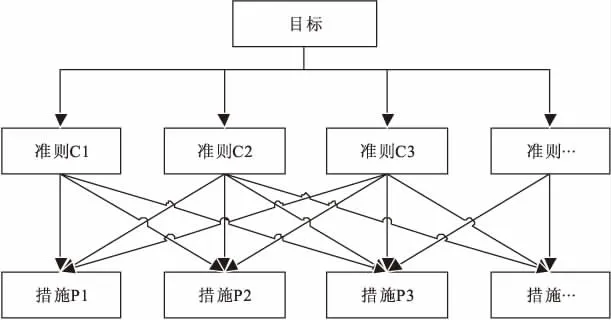
图1 AHP法的评价模型结构
1.2 指标空间权重算子的生成
指标空间权重算子的建立分四步[4]。第一步:根据层次分析法得到的评价层次结构模型可以构造判断矩阵。第二步:进行判断矩阵一致性检验。第三步:若判断矩阵通过一致性检验,则计算各指标的权重。第四步:通过各指标的权重构建希尔伯特指标空间权重算子Δ

1.3 标准希尔伯特指标子空间的建立
一般影响大坝安全的因素分为强度因素、管理因素、稳定因素三类;各因素都包含坝体、厂房、库岸三种评价指标[2]。大坝安全主要的评价指标包括三大类三小种[5]。其中每一种评价指标代表指标空间的一维,则构建一个3维的希尔伯特指标空间H3。若Hilbert指标空间的一个量化线性子空间为N。可得各指标元素向量y为[6]:

其中,e={e1,e2,e3}是的一组 H3标准正交基。在 H3中元素 y向量的坐标为:y={λ1,λ2,λ3}。若赋有权重的标准子空间 M 为Hilbert指标空间H3的另一个线性子空间[8],则设x为M的元素,存在映射Δ,使:
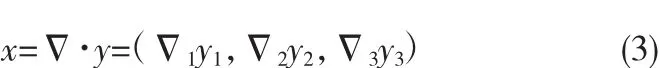
式(2)代入式(3)得:

则构造的M为三维的标准Hilbert线性指标子空间[8]。
2 基于M的安全指数向量范数评价模型
2.1 计量模型的建立
该模型的大坝安全评价模型各评价指标的关联性较低。根据其数乘性质可以构建单位球面,即为安全指标向量[6~7]。Hilbert空间性上弱紧性,则可用安全指数向量的范数‖M‖来表示大坝安全状况W的高低[8],即安全指数函数:W=‖M‖。
大坝安全评价建模步骤见图2。
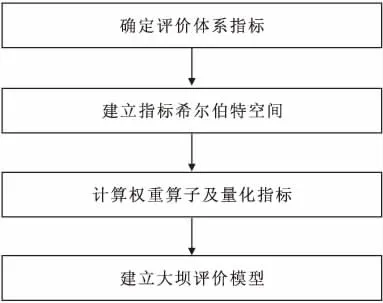
图2 评价模型建立过程
而‖M‖又是标准指标子空间的函数,可以表示为

则指标指数函数为
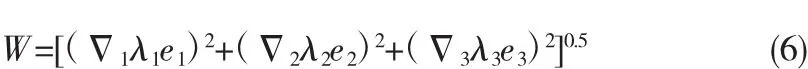
依据以上模型可以确定评价指标的数值,进而可以进行定性定量地判断大坝安全状况。而且可以对比不同指标对大坝安全等级的影响。经工程实际计算,大坝安全等级与分值区间的关系见表1[9]。

表1 大坝安全水平等级
2.2 安全指标分析
根据上文,大坝安全水平等级可以由安全指数模型确定,但实际问题依然不能解决。故根据指标分析的理论,对指标空间的每个指标计算评价,进而定量地确定各评价指标对大坝安全运行的影响状况[10]。所计算出的数值也称评价指标的贡献率。该模型对多元函数求偏导建立各指标的安全评价函数。则对式(6)求偏导得:
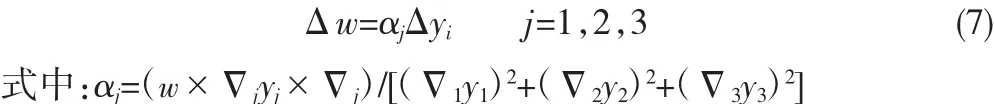
利用变化量便能确定出各个指标对大坝安全水平的影响。在实际应用中可以判断各个指标的重要性及影响大坝安全的因素,这样可以有目的性地提高某个指标的安全水平。
3 计算案例
3.1 安全指数的计算
现以某坝为例,该坝对强度、管理、稳定三个准则的价值取向为:首先要求强度好,然后要求管理水平高,最后才是稳定好。判断矩阵采用1~9比较尺度构造[11],且重要性等级与判断矩阵元素αij的取值见表2[12]。

表2 重要性等级与判断矩阵元素αij的取值表
由表2可得准则层对目标层的判断矩阵(依次为强度、稳定、管理因素)G为:

在计算权重之前应该进行矩阵的一致性检验。一致性检验的计算方法为:

式中:C.I.=(λmax-n)/(n-1);R.I.为平均随机一致性指标。
且当C.R.<0.1时,判断矩阵具有可接受的一致性,否则判断矩阵偏离一致性过大[12]。经计算判断矩阵G的C.R.<0.1,说明判断矩阵G满足一致性检验。
通过监测资料和大坝运行情况综合分析得,厂房安全指标P1、坝体安全指标 P2、库岸安全指标 P3分别为 99、97、95。并且根据该坝实际每部分运行情况对比各部分应达到的安全运行标准状况评价为:厂房的强度条件较好,稳定条件一般,管理水平中上;坝体的强度条件最好,稳定条件较差,管理水平中下;库岸的强度条件较差,但稳定条件好,管理水平高。
根据希尔伯特指标空间,将上述厂房安全指标P1、坝体安全指标P2、库岸安全指标P3数值代入式(4),可得
由层次分析法判断矩阵G和上述该坝实际每部分运行情况对比各部分应达到的安全运行标准状况评价可以计算得到坝体安全指标、厂房安全指标、两岸安全指标3个因素对大坝安全运行的影响程度,通常称作不同指标的重要程度。主要指标的重要程度见表3。

表3 主要因素总体影响程度优先级排序
权重算子由层次分析法的计算结果确定,即Δ=(0.1974,0.5059,0.2971)
上述计算得到x和Δ后,根据式(7)计算得到该坝的安全运行指数W=59.9。
由表1可得,该坝安全等级是一类坝;与该坝的最近一次大坝安全鉴定的结论一致。且厂房安全指标P1、坝体安全指标P2、库岸安全指标P3对大坝安全运行组合权重由表3可知,分别为0.20、0.50、0.30,符合水库大坝结构的实际运行规律。
3.2 安全指标贡献率的计算
由式(9)可以计算各个指标对该坝安全运行的贡献率。通过计算得到该坝的指标弹性算子:α=(0.06,0.42,0.14)。各指标变化Δyj取为1,则各指标对大坝运行总安全指标的贡献率为:ΔW=(0.06,0.42,0.14)。
故可得厂房安全指标P1、坝体安全指标P2、库岸安全指标P3对大坝安全运行的贡献率分别为0.06、0.42、0.14。与层次分析法得到的各个安全指标综合权重的规律一致,并突出了坝体安全指标的重要性,而库岸安全指标及厂房安全指标的贡献率则依次次之。
根据多层次分析法定量地计算安全指数和安全指标贡献率,为水库大坝实际运行维护提供了理论依据。说明基于希尔伯特空间多层次安全评价模型的计算结果可靠可信。
4 结论
影响水库大坝安全正常运行的因素很多,并且全面选取影响水库大坝安全运行的评价指标比较困难,所以建立比较可靠合理且计算简便的评价模型也相对困难。本文运用层次分析法可将不同层级的评价指标进行合理量化,把量化的评价指标空间构建为权重算子,然后依据希尔伯特空间向量范数理论对水库大坝安全性进行评价。通过实例计算验证,该安全评价模型的评价结果合理可信,可应用在水库大坝,包括一般水工建筑物的安全评价。
在实际工程应用该评价模型时,需要根据不同坝型运行的环境和特点及各种工况选取不同的大坝评价指标,构建不同层次的模型结构和维数不同的希尔伯特空间,以便更合理地评价大坝运行的安全状况。
