孟底沟水电站坝址区初始渗流场反演分析

唐少龙，汪 庆，罗梓茗，熊 威，万小强

（江西省水利科学研究院，江西 南昌 330029）

渗流对水利水电工程稳定与安全有着重大影响，在我国西南地区水电工程中更为显著[1]。工程研究表明，工程初始渗流场分布情况的合理与否是进行工程渗控系统效果评价分析的前提，而在坝址区大范围内通过钻孔获取地下水位得到渗流场不经济、不现实。基于此，本文采用正交设计、稳定渗流正分析、BP神经网络和遗传算法优化相结合的初始渗流场反演方法[2~3]，建立坝址区渗流场反演三维有限元模型，以长观孔监测值为目标函数，获取最优边界值得到初始渗流场分布特征。

1 反演分析方法

具体流程图见图1。

图1 渗流反分析流程

1.1 正交设计

正交设计是通过正交表合理安排和分析多因素的一种数理统计方法[4]，该方法在众多参数组合中安排数量较少的组合方案，从而大大减少反演计算的工作量。在初始渗流场反演分析中，参数对应为水头边界的取值情况。通过正交设计合理安排神经网络所需的水头边界取值组合方案。

1.2 稳定渗流正分析

针对正交设计得到的水头边界组合情况，采用signorini型变分稳定渗流分析方法[5]正分析模拟其渗流场，得到钻孔处水位样本数据，为后期建立神经网络的输入、输出映射关系提供数据支持。

1.3 BP神经网络

采BP神经网络是按照误差反向传播算法训练多层前馈神经网络，是目前为止使用最广泛的一种神经网络模型，能够建立较强的输入与输出的非线性映射能力[6]。本文输入层为边界水头组合值，输出层为各钻孔处水头值。

1.4 遗传算法优化

利用遗传算法优化的目的是在水头边界可能的取值范围内，寻找一组最佳的水头边界值的组合，使得各钻孔处水位实测值与计算值吻合最优。遗传算法原理是对达尔文生物进化论的自然选择和遗传学机制进行模拟，在参数组合的取值范围内进行全局搜索寻优的一种方法[7]。首先在参数组合范围内生成一系列可能的解作为初始种群，然后利用遗传操作生成新的种群，使得种群不断适应更高的方向发展[8]，当最优个体适应度达到某一阀值时计算结束，该个体即为最佳边界参数组合。

2 工程应用

2.1 工程概况

孟底沟水电站坐落于四川省境内雅砻江干流中游河段上，是雅砻江中游两河口~卡拉河段“一库七级”开发方案中的第五个梯级，上游是楞古水电站梯级，下游是杨房沟水电站梯级。大坝坝型是混凝土双曲拱坝，坝顶高程2259.0 m，最大坝高201.0 m。水库正常蓄水位2254.0 m，总库容为8.680亿m3。由于自身调节库容相对较小，仅能对入库径流进行日内调节，当与中游龙头水库两河口联合运行时可发挥多年调节作用[5]。

2.2 有限元模型

为满足分析需要，根据工程坝址区地质地形条件，工程地质图等资料，建立孟底沟水电站坝址区整体三维有限元模型，模型采用六面体等参单元进行剖分，共划分单元53256个，节点数54456个，如图2所示。模型计算范围以河道中心线坝轴线处为中心，分别向左右岸延伸1000 m，向上下游各延伸400 m和1000 m，其中上游侧左岸边界距孟底沟沟口约100 m。

图2 坝址区三维有限元模型

2.3 计算参数与边界

由于电站坝址区山体起伏较大，在反演分析初始渗流场分布情况时，需充分考虑边界水位分布清情况受地形起伏变化的影响。模型四个角点处水位为待反演值如图3所示，相应的地下水位埋深值分别为ΔH1，ΔH2，ΔH3和ΔH4，四周其他位置处的水位情况通过地形走势插值获得。由于坝址区长观孔水位观测资料有限，选取6个典型长观孔水位观测值，具体水位见表1。

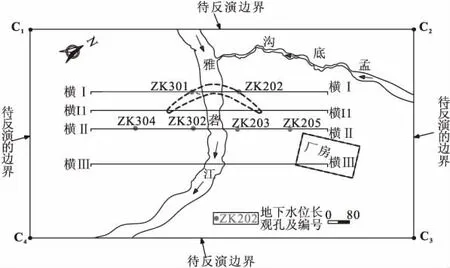
图3 渗流场反演边界示意图

表1 长观孔的地下水位监测资料

坝址区渗透特性分区的合理性与渗透系数取值的准确性是进行渗流有限元计算的基础。根据坝址区钻孔压水试验结果，坝区岩体渗透性与岩体风化卸荷，蚀变岩带、蚀变岩集中带分布以及构造关系密切，岩体渗透性主要分为5个区，分别为强卸荷带岩体为强透水区、弱卸荷带岩体为中等透水区、弱透水偏强区、弱透水偏弱区、微透水区，各渗透分区取值见表2。

表2 渗透特性分区描述及其渗透参数的取值

3 渗流场反演结果

通过采用正交设计、稳定渗流正分析、BP神经网络和遗传算法优化相结合的初始渗流场反演方法，并综合考虑坝址区地形起伏变化及长观孔水位观测资料，获得了坝址区计算区域内反演模型四个角点处的埋深取值分别为ΔH1=252.01 m，ΔH2=89.56 m，ΔH3=275.10 m和ΔH4=16.66 m。通过四个角点处情况，根据山体起伏可获得四周边界水位分布情况，再采用稳定渗流正分析方法计算得到坝址区的初始渗流场分布情况，如图4所示。从图中可以看出，通过反演得到的渗流场分布特征，地下水水位分布情况山体的起伏形态基本一致，在河道存在一定溢出，分布特征总体上较符合实际情况。

图4 孟底沟初始渗流场及边界水位分布图

反演计算得到的各钻孔位置处水头值与相应钻孔位置实测值的对比见表3及图5，从反演值与实测值的对比图可以看出各钻孔水位反演值与相应钻孔位置水位实测值较为接近，长观孔水头误差绝对值的平均为5.15 m，反演计算得到的坝址区初始渗流场整体上能够反映出坝址区初始渗流场实际的分布情况。图6给出了横II-II剖面两岸山体地下水位自由面，由图可知，左岸的地下水位较右岸的低，自由面坡降也相对较缓，与山体走势较为一致，说明勘探获得的各地层渗透特性参数的取值大小与实际情况较为吻合，反演计算得到的初始渗流场分布情况能够满足后期渗流计算的需要。

表3 长观孔地下水位观测值和计算值对比 单位：m

图5 长观孔地下水位误差分析图

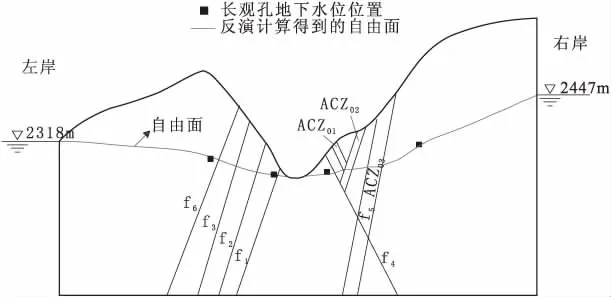
图6 横II-II剖面两岸山体地下水位反演分析结果

4 结论

1）由于长观孔观测资料有限，渗流场边界水位的确定具有一定的主观性和误差。采用正交设计、稳定渗流正分析、BP神经网络和遗传算法优化相结合的初始渗流场反演方法，结合观测水位及地形起伏，所得观测孔计算水位与实测水位误差较小，反演结果与实际较为吻合，反演分析方法合理有效。

2）本文计算所得初始渗流场误差较小，计算结果可为工程后续渗控系统有效性评估提供重要参考。但在工程实际情况中，普遍存在裂隙、断层，其对工程渗透系数产生显著的各向异性，本文尚未考虑其作用，需在今后做进一步的研究。