钢混框架振动的NLFEM分析和ADRC主动控制

王善伟，韩爱平，朱军强，王社良

（1.西安建筑科技大学 土木工程学院，西安 710055；2.长安大学 信息工程学院，西安 710064）

结构振动主动控制是通过对环境干扰与结构反应的准确测量，采用现代控制理论的主动控制算法在精确结构模型基础上运算和决策出最优控制力，最后使作动器在很大的外部能量的输入下输出最优控制力[1]。学者高志强[2]将诸多主动控制算法如线性二次型控制算法、H控制算法、滑移模态控制算法等归属于模型范式，即这些算法需要被控对象具有精准的数学模型。而实际工程中被控结构的非线性特性不容忽略，其结构模型很难准确获取，对于钢筋混凝土结构更是如此。因而有必要寻求一种适用性广、不依赖于被控对象精确模型的控制算法。

自抗扰控制策略(Auto Disturbances Rejection Control，ADRC)是工业界广泛运用的PID控制技术的改进[3]。其不依赖于精确数学模型，继承了PID控制基于偏差来消除偏差的思想精髓，将作用于结构的内扰和外扰归结为“总和扰动”，并对这个扰动实时跟踪并进行估计补偿。本文采用遗传算法对ADRC控制器参数进行分步整定优化，将通用有限元软件ANSYS作为主动控制主仿真平台以分析结构在外扰与控制力作用下的反应，代替simulink对结构反应的计算，建立某5层RC框架非线性有限元模型（NLFEM），最后采用ADRC控制策略对被控结构模型进行主动控制仿真。

1 ADRC控制原理及结构振动控制多变量解耦

从完成控制的目的来看，如果某种扰动不影响系统的被控输出，则在控制过程中就不用考虑消除这种扰动的影响，需要消除的仅仅是能够影响被控输出的那种扰动；既然某种扰动能够影响被控输出，则该扰动的作用就能够在被控输出的观测信息中估计提取出来，从而就可以采用适当的方法补偿或消除这种扰动的影响[4]。自抗扰控制器具有能够“实时跟踪估计扰动并补偿”特性根本上的形成机理正在于此。韩京清将其组成分为三个模块[5]，控制器系统框图如图1所示。

图1 ADRC控制系统框图

由于结构振动控制目标值为0，不会发生阶跃突变，无需安排过渡过程，所以可以省去TD模块。在结构振动2阶控制系统(1)中，f0(v1,v2)为扰动中的可建模确知部分，则该系统的自抗扰控制算法[4]为

（1）以系统输出y和输入u来跟踪估计系统状态和未知扰动的扩张状态观测器(ESO)

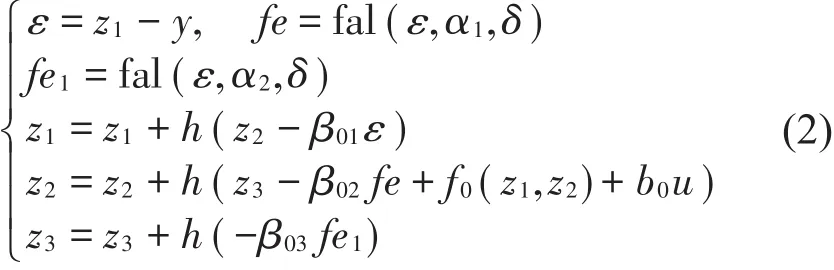
式中：h为积分时间步长，β01、β02、β03为待定参数。

（2）非线性状态误差反馈律(NLSEF)

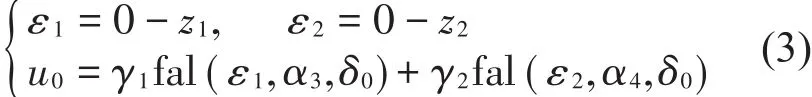
（3）扰动的补偿过程

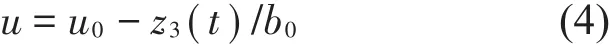
其中fal(e,α,δ)具体形式为

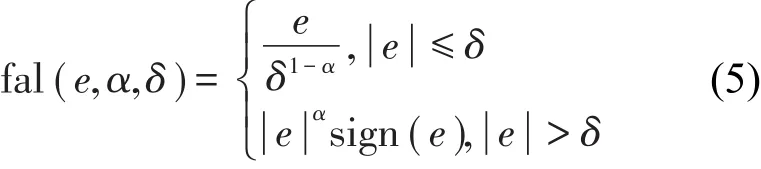
对于具有n个平动自由度的结构，地震作用下主动控制运动方程可以表述为

式中：{X(t)}∈Rn为结构位移向量，[FC] {X(.t)}是阻尼力向量，[Fk] {X(t)}是恢复力向量；假定结构中安装有P个作动器，[U(t)] ∈RP为控制力向量，[BS] ∈Rn×P是相应作动器位置矩阵。建筑结构振动控制系统是多输入-多输出系统，第i个作动器的出力对第j路的位移输出存在影响，这种现象叫做耦合。而自抗扰控制器主要用于单输入-单输出系统，因而应用时需要进行解耦。

对式(5)进行变换

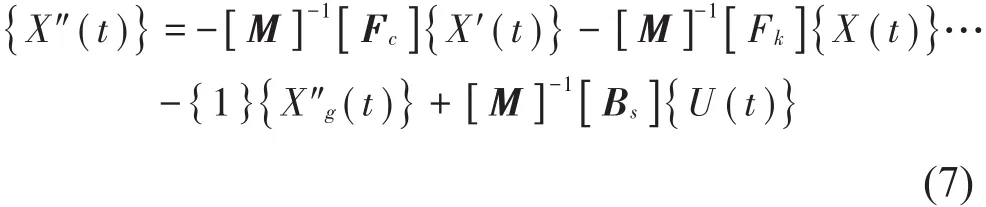
可以把地震作用看做成外扰动，结构阻尼力和恢复力看成是内扰动，则总和扰动即为

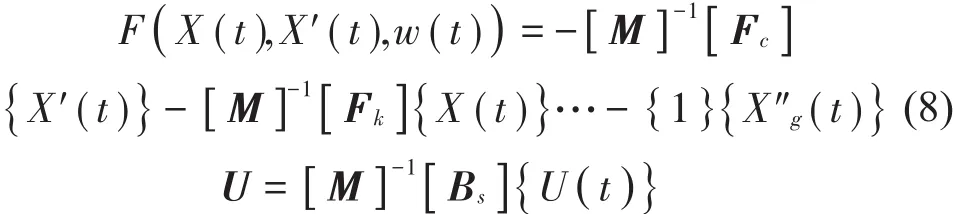
从而

其中：w(t)代表结构受到的不确定扰动，U为虚拟控制量，引入，可以将p输入-n输出系统的矩阵表达式(8)写为

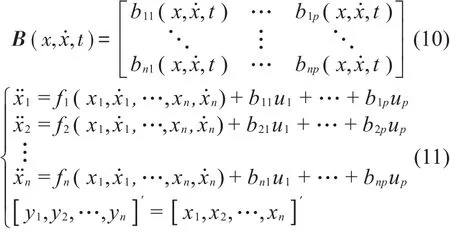
输入量uj系数bij的含义是第j个作动器出力对第i路输出的影响系数，是系统状态变量与时间的函数，当作动器位置一定时，控制力输出对结构影响是一定的，可写为

韩京清[4]将控制力之外部分称为“动态耦合”部分，虚拟控制力U称为“静态耦合”部分，且“动态耦合”部分各分量已经在解耦控制中作为各通道上的总扰动估计补偿掉了，且对“静态耦合”部分只要矩阵可逆或在其附近找一个可逆矩阵来近似，便可通过虚拟控制力U推导出实际控制力u=[u1,u2,…up] 。

2 遗传算法参数整定及ANSYS控制仿真实现原理

用于结构振动控制的ADRC控制器待优化参数：ESO模块参数β01、β02、β03；NLSEF模块参数γ1、γ2；扰动补偿参数b0，见图2。应用控制器设计分离性原理[4]。同时采取分步整定优化的方法[6]，既首先对ESO在开环状态下进行参数整定优化，获得β01、β02、β03参数值，之后再对NLSEF参数γ1、γ2进行寻优，进而获得性能良好、适用于建筑结构振动控制的ADRC控制器。

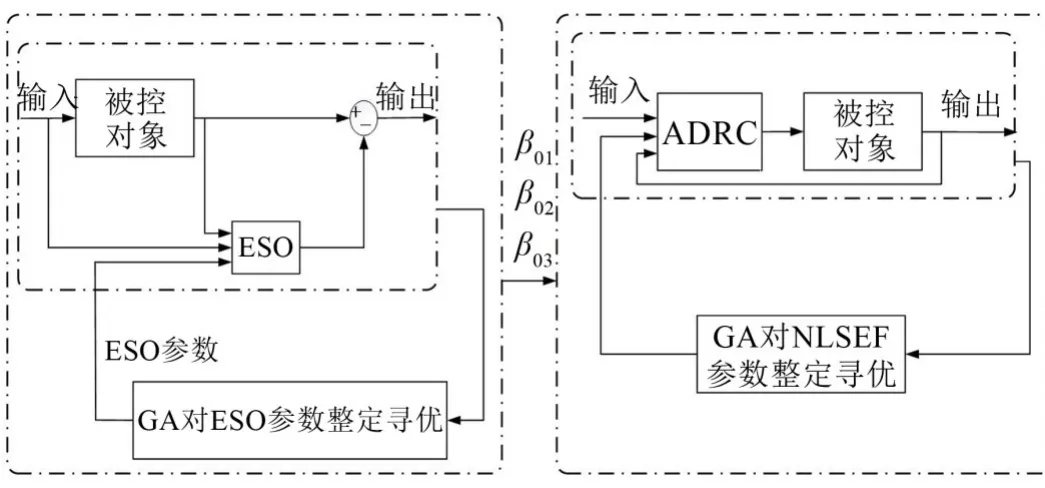
图2 ADRC参数优化示意图

优化具体步骤：

ESO参数优化的适应度函数表达式为

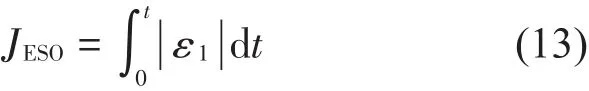
式(13)中ε1=0-z1表示位移的跟踪误差，文献[6] 中同时考虑归一化后3个状态(位移、速度和总扰动)的跟踪误差并不合理，由于3个状态峰值的数量级相差很大，而归一化正是以峰值作为基数，峰值大，归一化后的误差小；峰值小，归一化后的误差反而大，因而归一化后寻优效果并不理想。3种误差的变化同步，于是仅考虑位移误差即可。将得到的β01、β02、β03作为 ESO 模块参数，进行参数γ1、γ2的优化，适应度函数为

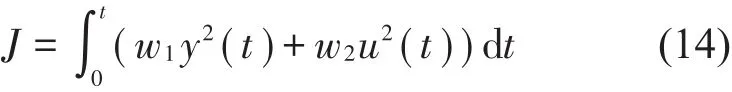
y(t)与u(t)分别为振动位移与控制力输入，w1与w2为相应加权系数，以同时兼顾位移控制效果与出力的大小，根据文献[7] ，位移和控制力的加权系数分别取值为8和1×10-6。

为实现通用有限元软件ANSYS主平台下的主动控制仿真，具体实现过程参考文献[7] 制定并作相应改进。即通过MATLAB编程实现ADRC算法，通过ANSYS编程实现主体分析过程，建立一个flag标志文件，当flag=0时运行ANSYS，此时MATLAB处于暂停状态，当flag=1运行MATLAB，同时ANSYS处于暂停状态。根据flag值的不同，循环运行相应的软件，直到flag值改变为2时结束循环，两个软件结束运行。ANSYS控制仿真运行流程框图如图3所示。

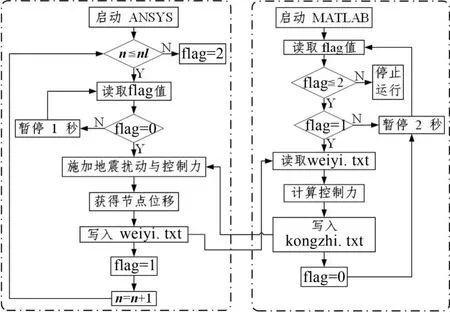
图3 ANSYS控制仿真实现框图

3 数值模拟实例

3.1 RC框架NLFEM建立及可靠性验证

为验证ADRC控制器对建筑结构振动控制的理论可实现性，本文对抗震设防烈度为8度地区某5层RC框架进行冲击荷载与罕遇地震作用下主动控制模拟。框架层高3.9 m，坐标轴X方向有2跨，总跨度为8.4 m，Y方向有2跨，总跨度为7.2 m；X方向和Y方向的梁截面分别采用200 mm×500 mm和200 mm×400 mm矩形截面，板厚度为100 mm，柱截面采用400 mm×400 mm矩形截面。混凝土为C30混凝土，钢筋为HRB335和HPB235两种。结构所在地区设计基本加速度为0.2 g，梁板柱均按相应设计规范进行配筋。

在ANSYS有限元中采用整体式模型[8]建立RC框架非线性有限元模型（NLFEM），使用SOLID65实体单元对梁板柱进行网格划分，不考虑钢筋与混凝土粘结滑移，通过单元实常数设置来实现梁板柱中的钢筋的弥散配置。框架整体NLFEM如图4(a)所示，有限元模型中混凝土材料定义为文献[8] 中的多线性等向强化模型(MISO)，并在其中的数据中去掉曲线下降段。钢筋材料定义为双线性等向强化模型(BISO)，材料的单轴应力-应变关系曲线如图5(a)和图5(b)所示。混凝土材料的密度ρ=2551 kg/m3，泊松比μ=0.2，钢筋混凝土楼板上均布恒荷载为6 kN/m2，对楼板密度进行折算，折算后密度为ρ=8551 kg/m3。

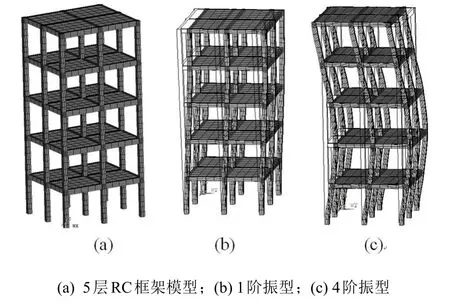
图4 结构模态分析

分析结构模态，第1和第4阶模态如图4(b)、图4(c)所示，可以看出这2阶模态以水平Y方向振动为主，对应自振频率为f1=1.4009 Hz，f4=4.3615 Hz，在式(6)中，假定前2阶阻尼比为0.05，采用比例阻尼C=α1M+α2K可得阻尼矩阵[C] ，[Fk] {X(t)}为结构振动非线性恢复力，本文采用Bouc-Wen恢复力模型[9]，并基于该模型形成5层RC框架的非线性恢复力模型，其中第i层恢复力描述为

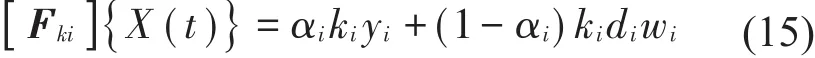
其中：yi为第i层的层间位移，αi、ki、di分别为第i层屈服前后刚度比值、初始弹性刚度、层间相对极限屈服位移。对该单层框架中柱顶点沿坐标轴Y方向位移加载，可得该单层框架滞回曲线，提取可得ki=2.5326×107N/m，di=0.0612 m(i=1,2,3,4,5)，wi为恢复力模型无量纲参数，表达式为

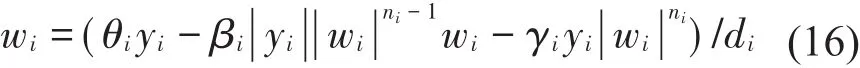
式中θi、γi、βi、ni为结构滞回曲线形状控制参数，可根据该单层框架滞回曲线并采用遗传算法对参数进行整定，认为每层参数相同，整定后参数：θi=1.6、αi=0.3、βi=10.56、γi=2.88、ni=12(i=1,2,3,4,5,6)。将上述层间恢复力模型写入MATLAB自编S函数代码程序，封装成S-Function模块，再与其他仿真功能模块共同形成该5层RC框架基于Bouc-Wen恢复力模型SIMULINK弹塑性动力时程仿真模型。

分别对上述模型的弹塑性动力时程分析Y向输入PGA=400 gal的El-centro波，图6为框架首层位移和速度反应，可以看出根据ANSYS有限元与根据SIMULINK仿真得到的楼层位移/速度反应在一定程度上拟合较好，验证了有限元模型的可靠性。

3.2 ADRC控制器参数寻优

将上述Bouc-Wen恢复力模型S-Function模块与其他SIMULINK模块搭建成遗传算法优化ADRC控制器参数的平台。ESO与NLSEF模块参数取值为

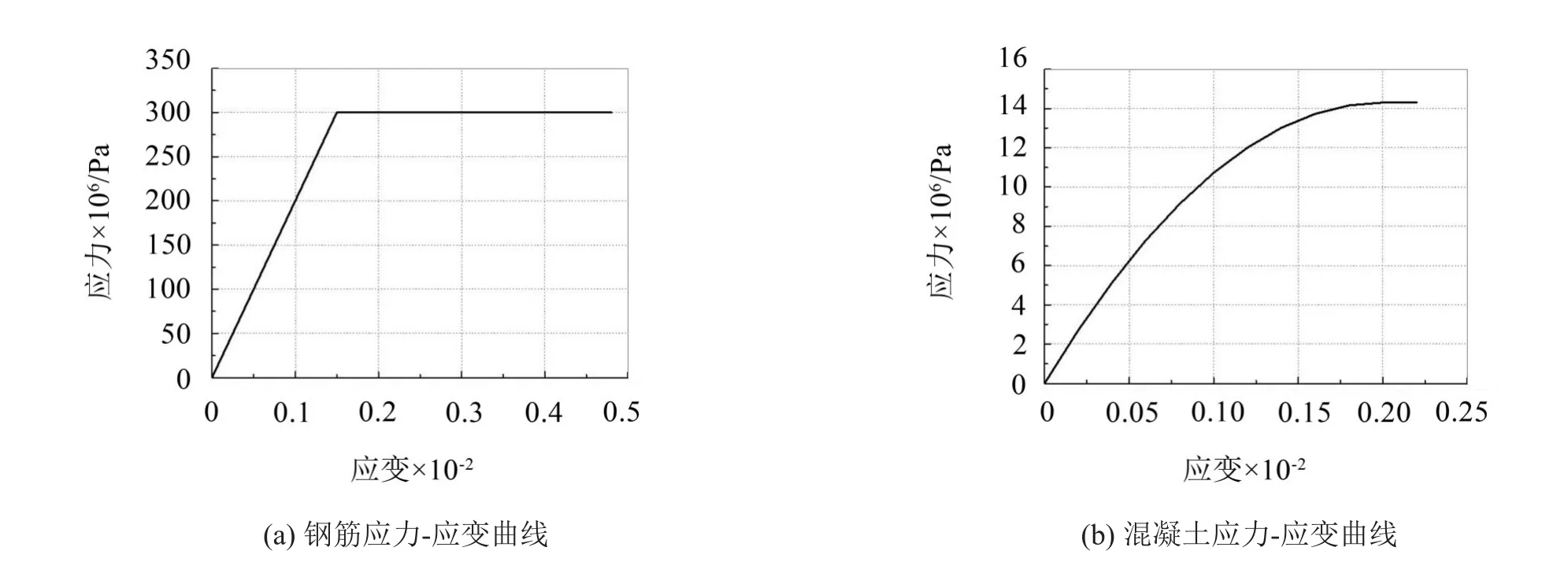
图5 材料的单轴应力-应变关系曲线

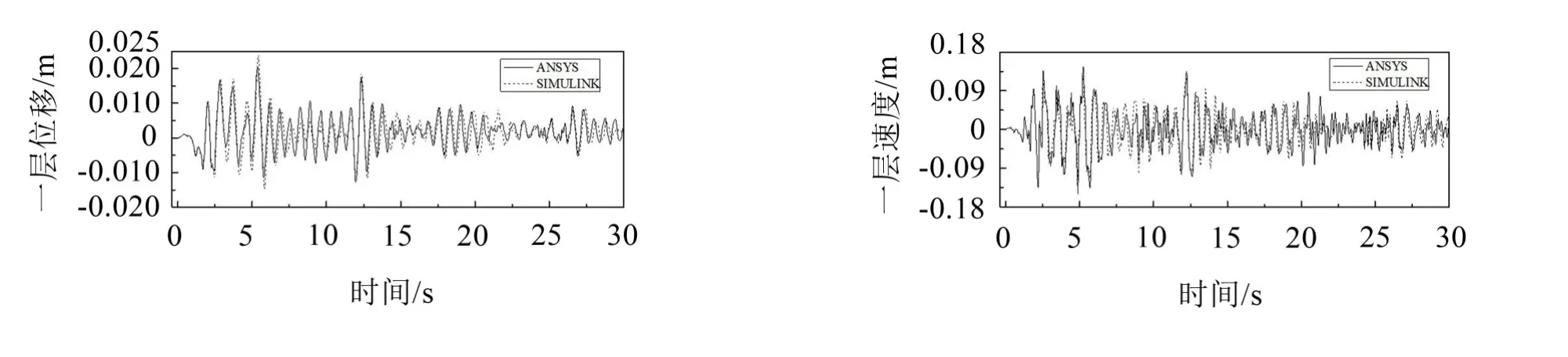
图6 El-centro波首层位移/速度时程

进行遗传算法优化时外扰选择为PGA=400 gal的 Taft波 ，图 7(a)与 图 7(b)为 参 数β01、β02、β03、γ1、γ2寻优SIMULINK模型图。其中β01=897、β02=857.36、β03=3857.8、γ1=39.5、γ2=35.4。

外部可调参数b0取值为300。

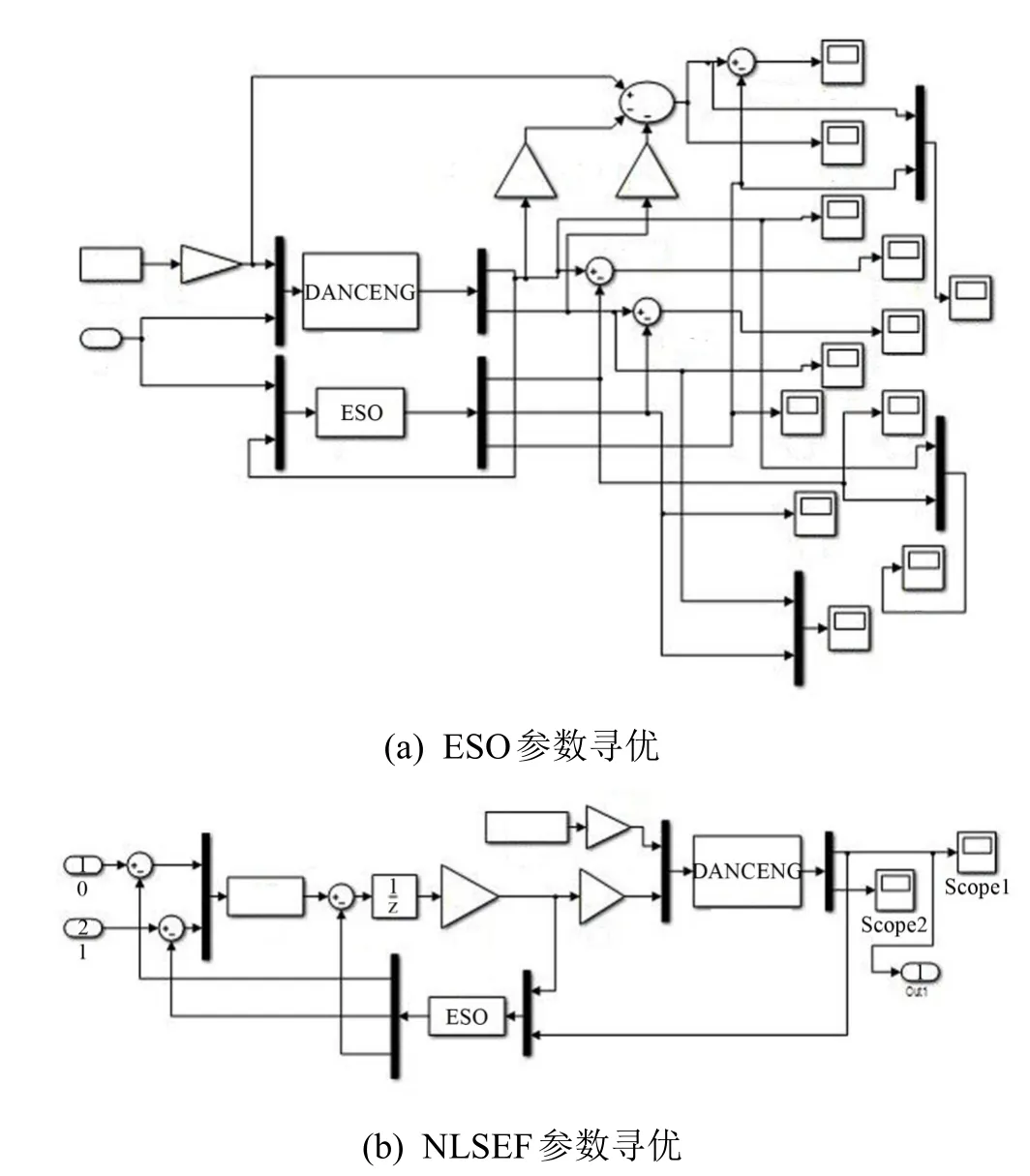
图7 参数寻优的SIMULINK模型

3.3 ANSYS控制仿真

以ANSYS为主仿真平台，分别选取PGA=200 gal的冲击加速度、PGA=400 gal的Taft波、天津波、兰州人工波在Y向输入RC框架NLFEM，每种外扰工况下控制仿真又可分为有控制和无控制两种工况。(注：各图中的曲线A代表有控制工况，曲线B代表无控制工况)。

主动控制力可由主动质量阻尼控制系统施加,但本文主要研究ADRC控制器在考虑建筑结构非线性振动主动控制模拟时的算法可实现性，不对驱动器做深入设计，但在此对驱动器出力能力进行限制，假定驱动器最大出力为400 kN，楼层最大位移小于0.0001 m，且最大速度小于0.002 m/s时，驱动器停止运行。

(1)PGA=200 gal的阶跃荷载

在ANSYS平台上，在t=0 s施加PGA=200 gal的加速度冲击，采样时间步长为0.02 s。从图8中可以看出，冲击荷载作用下，未控工况下，t=7 s时结构尚有较小振动；ADRC有控工况下，t=1 s时结构已经没有轻微振动，振动收敛较快，控制效果明显。

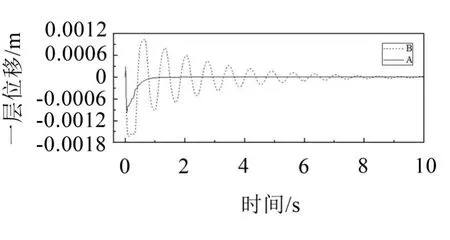
图8 冲击荷载作用下一层有控位移

(2)PGA=400 gal的Taft波、兰州人工波、天津波

考虑结构体系塑性，在某些特定地震荷载作用下，体系屈服后将不会在其初始的平衡位置附近震荡。屈服引起体系的位移偏离其初始平衡位置，体系在新的平衡位置震荡，直到下一次屈服时，此平衡位置改变，因此在地面停止震动后，体系通常将最终停留在与其初始平衡位置不同的位置上(即保持永久变形)[10]。无控制时，在Taft波、兰州人工波输入下计算结果见表1，各层层间相对位移均小于前述Bouc-Wen恢复力模型中的层间相对极限屈服位移di，此时为弹性阶段振动，振动平衡位置为位移零点；而天津波输入下（见图11、表1），首层层间相对侧移d1超出极限屈服位移，此时为塑性阶段振动，振动平衡位置相对于位移零点发生偏移。

表1 位移绝对值峰值控制效果/10-2m

有控制时，3种地震波输入下，各层间位移均控制在较小范围（见图9至图12及表1），均小于层间相对极限屈服位移di，振动属弹性阶段，表明ADRC控制器具有良好的理论控制效果。

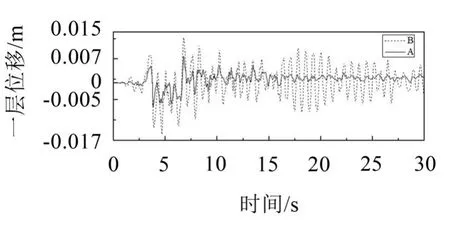
图9 Taft波作用下一层有控位移

图11 天津波作用下无控位移

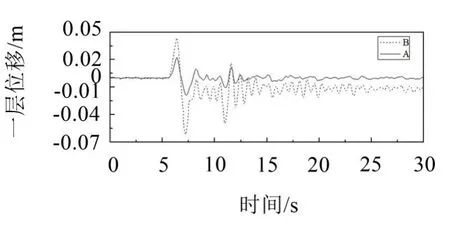
图12 天津波作用下一层有控位移

对比3种地震输入下ANSYS主仿真平台有控和无控峰值结果(见图13及表1、表2)，地震作用下各层的控制力峰值均小于200 kN，各层有控位移峰值均有很大程度减小，ADRC控制效果整体较为明显，天津波作用下体系位移有控与无控对比进一步说明ADRC控制器对结构振动控制的理论可实现性与理论控制效果。

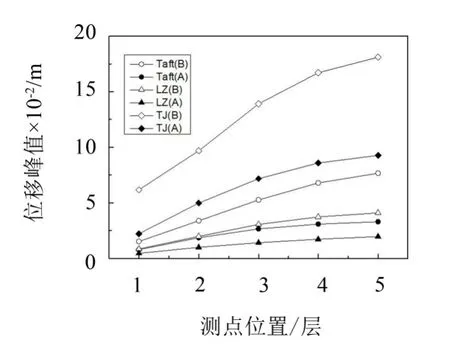
图13 位移绝对值峰值图

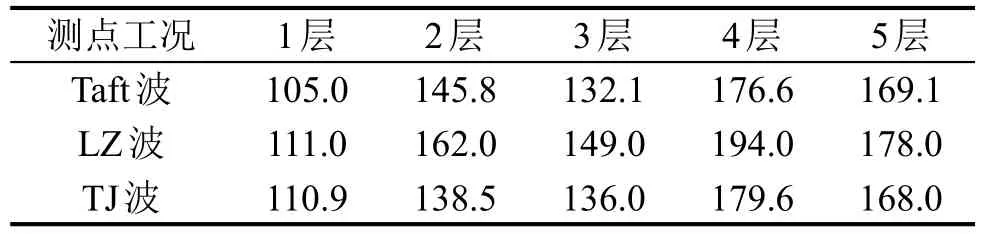
表2 控制力绝对值峰值/kN

4 结语

本文系统论述了ADRC控制器用于建筑结构振动控制时算法的改变，利用分离性原理和遗传算法对控制器参数进行分步整定优化，同时将通用有限元ANSYS作为结构振动控制主仿真平台，建立8度烈度地区某5层钢筋混凝土框架非线性有限元模型（NLFEM），最后在ANSYS中对被控结构模型进行阶跃荷载与地震波输入时的主动控制仿真，得出如下结论：

(1)通过仿真实验效果对比发现，ADRC控制器对于地震外扰抑制效果明显。通过输入阶跃荷载时结构振动无控和有控对比，可知ADRC控制器对于阶跃荷载的振动控制效果明显，振动收敛很快。外扰作用下良好的控制效果进一步说明ADRC控制策略的算法理论可实现性。

(2)在结构振动控制中应用ADRC控制策略存在控制器参数较多而整定较困难的问题，为克服这一不利因素，则源于过程控制、不依赖于被控对象精确模型的ADRC控制策略在结构振动控制的应用前景会十分广泛。

(3)考虑结构非线性条件下进行弹塑性控制时程分析，在某些外扰作用下，无控制时体系振动将会进入塑性阶段，体现在位移时程中其振动平衡位置将会偏离位移零点。

(4)以通用有限元ANSYS作为振动控制仿真的主运行平台，一定程度上扩宽了主动控制仿真实现途径，这不仅从理论上说明基于通用有限元软件平台考虑非线性条件下实现结构主动控制模拟的可行性，而且为主动控制技术研究提供了新思路。