傅里叶单元在航空发动机机匣强度振动分析中的应用
2019-08-27况成玉陆晓锋
况成玉,陆晓锋
(中国航发商用航空发动机有限责任公司,上海 200241)
关键字: 振动与波;变形与应力;航空发动机;机匣;傅里叶单元;仿真分析
机匣是航空发动机的重要零件,承担着固定静子叶片、传递发动机推力和与转子构成气流流道的重要作用[1],其力学特性对叶尖间隙、发动机临界转速等有着十分重要的影响[2]。机匣是具有旋转轴对称特征的构件,但由于安装等需要,这些机匣构件往往存在纵向螺栓安装边等非轴对称特征结构,如图1所示。
这些非轴对称特征对于机匣的应力、变形沿周向不均匀度和振动均存在不同程度的影响,这使机匣变形、应力和振动分析难度增加。
针对此类航空发动机机匣构件,建立有限元模型开展静强度和振动分析时,通常的处理方法[3-4]如下:
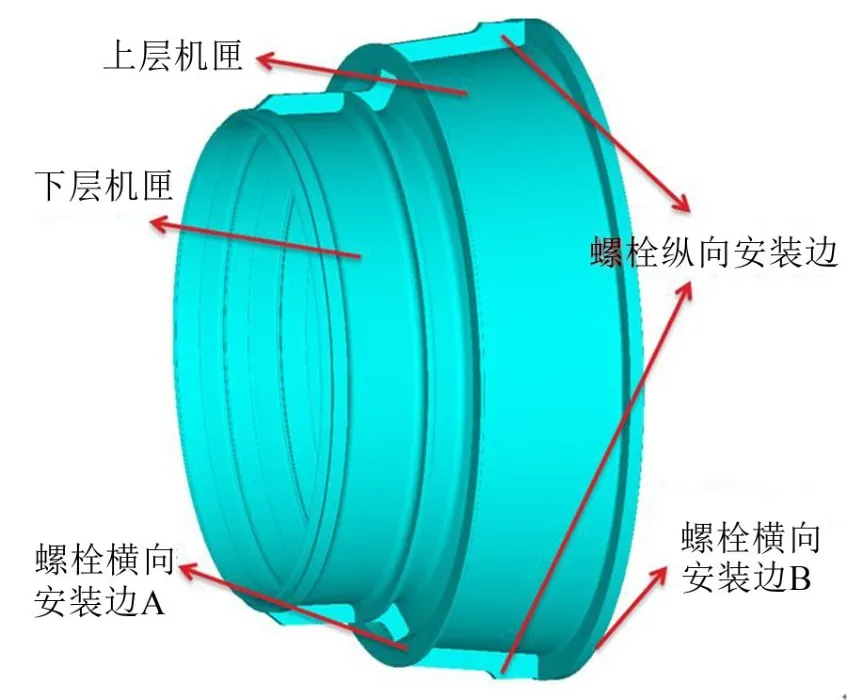
图1 某型航空发动机高压压气机机匣示意图
(1)建立二维传统轴对称机匣分析模型,即忽略纵向螺栓安装边等非轴对称特征,这是获得机匣纵向截面应力水平的普遍做法,但由于分析模型的限制,无法通过开展振动分析获得机匣的弯曲、扭转等共振模态,也无法分析由于纵向螺栓安装边等非轴对称特征带来的机匣变形沿周向的不均匀度;
(2)基于壳单元建立机匣分析模型,提取中面并利用壳单元模拟旋转对称部分和纵向安装边等特征,这适用于机匣振动和变形沿周向不均匀度分析,不适合计算机匣纵向截面的应力分布,同时当机匣截面厚度较大或者截面几何形状复杂时,也无法采用壳单元对如图3所示的复杂的机匣截面建模;
(3)基于三维实体单元建立机匣分析模型,这样可以充分考虑结构的几何特征,获得最为准确的结果,但建模复杂,需要具有较高的有限元网格处理能力,另外计算规模偏大,分析耗时,不符合工程设计的需要。
综上所述,针对具有旋转轴对称特征、但局部存在非轴对称属性的航空发动机机匣静强度和振动分析,现有分析方法不是由于计算规模较大而影响工程设计效率,就是由于分析模型限制无法全面获得机匣的应力、变形沿周向不均匀度和振动分析结果。
傅里叶单元是一种轴对称单元,但本质上还是二维单元,但相对于传统的轴对称单元,由于其特殊的形函数,傅里叶单元的节点位移可以沿周向按傅里叶级数展开,因此可以用于模拟三维构件的变形[5],如扭转、弯曲等,这是传统轴对称单元所不具备的,另外对于截面几何形状复杂的情况,也可以在不显著提高计算规模的前提下,对截面进行准确的建模,获得合理的分析结果。
基于某型航空发动机高压压气机延伸对开机匣,通过在傅里叶单元周向展开截面上设置轴向加强筋等措施,使二维傅里叶轴对称单元可以用于处理具有轴对称特征、但局部存在非轴对称属性(如存在轴向安装边)的航空发动机机匣应力、变形沿周向不均匀度和振动问题,并与二维传统轴对称和三维实体模型的计算结果进行了对比。
1 傅里叶单元的基本原理
设定ur、uz、uθ、Φr、Φz、Φθ为局部坐标系下的位移分量,将它们沿周向θ按傅里叶级数展开如下[1]
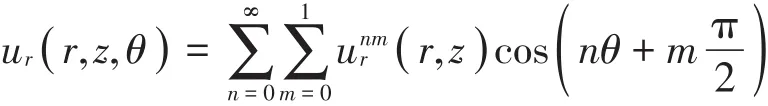
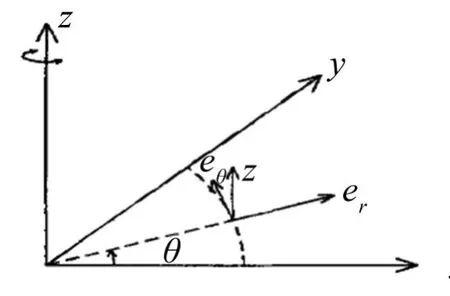
图2 坐标系定义

式中:n为波数,m为相位数。
每个谐函数(n,m)对应一个结构的基本变形。如(0,0)是沿旋转轴方向的拉伸,(0,1)是绕旋转轴的扭转,弯曲则表达为(1,0)和(1,1)。
在总体直角坐标系下建立二维傅里叶单元,每个节点有9个自由度,前6个自由度像梁单元一样,分别为沿旋转轴线方向的拉伸、扭转以及弯曲引起的其它2个轴线方向的线位移和角位移。另外3个自由度与旋转轴的横截面变形有关,分别为拉伸引起的径向位移和弯曲引起的两个切向位移。因此用这类单元可以很好地发挥二维单元计算规模小,却又可以模拟三维扭转、弯曲变形的优势。
2 压气机机匣计算结果
2.1 计算对象
以某型航空发动机高压压气机延伸对开机匣为研究对象,材料为GH4169,如图1所示。
该延伸对开机匣的结构特征包括:具有旋转对称特征,在0°和180°周向方向存在纵向螺栓安装边,分为上下两层,上层机匣通过横向螺栓安装边与其余机匣连接,下层机匣周向开槽以安装静叶扇形段。
分别采用二维传统轴对称单元、三维实体单元、二维傅里叶轴对称单元建立延伸对开机匣分析模型,如图3和图4所示,信息比较见表1。
为了使计算结果具可比性,3种分析模型的纵向截面单元网格均保持一致,其中三维机匣模型周向共计360份单元,二维傅里叶轴对称模型在0°和180°截面分别通过壳单元建立加强筋,来模拟纵向安装边。在3种分析模型中,忽略一些对整体结果
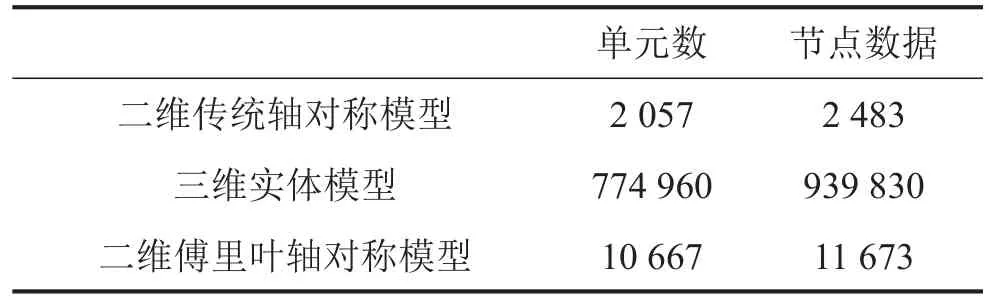
表13 种分析模型信息比较
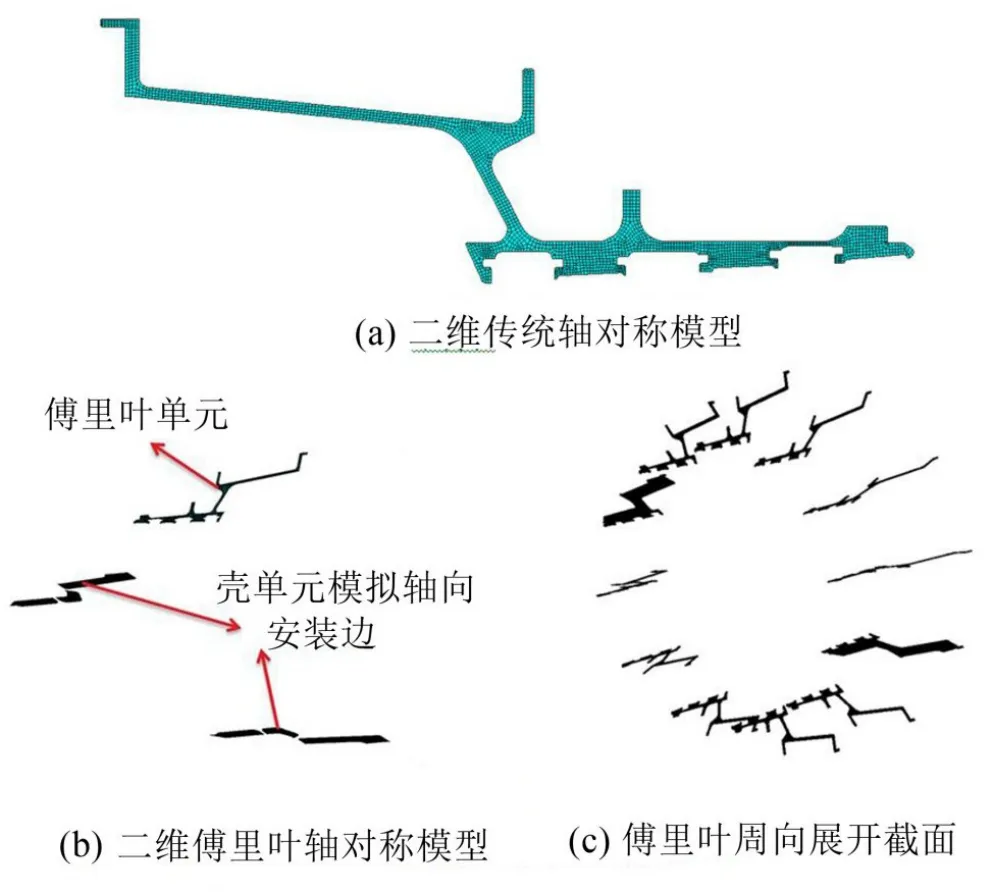
图3 延伸对开机匣二维有限元模型

图4 延伸对开机匣三维有限元模型
影响不大的细节特征,如安装边螺栓孔等。
该机匣静强度分析中考虑的主要载荷是:腔压、温度场、叶片轴向力和安装边A气体载荷,振动分析中考察其静频特性。
在位移边界条件方面,静强度分析时,约束该机匣横向螺栓安装边B的轴向和周向位移;振动分析时,约束机匣横向螺栓安装边A和B的轴向和周向位移。
2.2 机匣应力分析结果
基于如上模型和载荷,开展该延伸对开机匣的静强度分析,图5分别为3种分析模型的整体应力分布结果,其中二维传统轴对称模型和二维傅里叶轴对称模型结果均在360°周向上进行了扩展。
由图5可知,由于对开机匣纵向安装边的存在,三维实体模型和二维傅里叶模型的机匣截面应力均表现出了周向分布的不均匀性,这种应力不均匀的趋势也一致,而二维传统轴对称模型无法计算出应力沿周向的分布趋势。为了进一步考察这种不均匀性,针对三维实体模型和二维傅里叶轴对称模型,分别在周向提取0°和90°2个截面,考核如图5所示的圆柱面A位置上的最大第一主应力,并加以比较,其中0°截面为纵向螺栓安装边所在截面,90°截面远离该安装边。
由表2可知,在远离纵向安装边的90°截面,三维实体模型在圆柱面A上的最大第一主应力与二维传统轴对称模型的结果非常接近(相差不超过0.1%),小于二维傅里叶轴对称模型在圆柱面A上的应力值约21%,二维傅里叶轴对称模型的结果偏保守;在0°截面,即纵向螺栓安装边所在截面,由于安装边的加强作用,三维实体模型和二维傅里叶轴对称模型在圆柱面A上的最大第一主应力均有所降低,两者相差约30%,且二维傅里叶轴对称模型的应力结果偏保守。
另外3种分析模型,在同一个电脑计算平台下(16 G内存,Intel E52.80 GHz),计算耗时对比如表3所示。

图5 机匣第一主应力分布图

表2 机匣最大第一主应力(分别以三维模型在0o和90o方向的最大应力为基准进行归一化)

表33 种分析模型的静强度计算耗时对比/min
从表3中可知:二维傅里叶轴对称模型较二维传统轴对称模型,计算耗时仅增加了2 min,而相对于三维实体模型,其计算耗时大大降低。
2.3 机匣变形沿周向的不均匀度分析结果
在2.2小节延伸对开机匣静强度分析结果的基础上,考察机匣径向变形沿周向的不均匀程度,其中重点评估动叶叶尖对应机匣A、B和C 3个位置的径向变形,如图6所示。
提取截面A、B和C沿周向的最大和最小径向变形数据,见表4。
由于二维传统轴对称模型无法考察变形沿周向不均匀度,因此本节重点对比三维实体和二维傅里叶轴对称模型的径向变形沿周向不均匀度。

表4 机匣径向变形计算结果(以三维模型的最大变形为基准进行归一化)
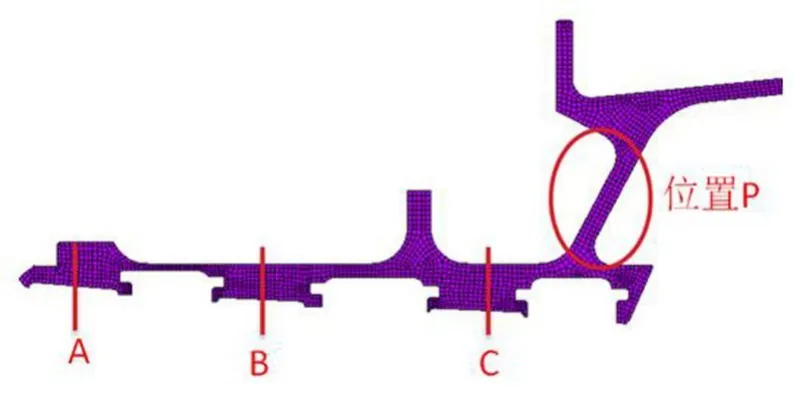
图6 机匣变形沿周向的不均匀度考核位置示意
通过以上分析可知,由于纵向螺栓安装边的影响,对开机匣沿周向方向的径向变形分布不均匀,通过比较可知,二维傅里叶轴对称模型在3个截面A、B和C计算出来的最大和最小径向变形与对应三维实体模型的变形结果非常接近(相差不超过1%),如图7所示。

图7 对开机匣径向变形分布图
该结果可以为机匣变形椭圆度对气动性能的影响评估提供支撑;A位置的最小和最大径向变形的差异大于其余位置,这与该对开机匣特殊的结构形式有关,由于上下层机匣过度区域P的加强作用,C位置的径向变形沿周向要更均匀。
2.4 机匣振动分析结果
基于此延伸对开机匣的三维实体和二维傅里叶轴对称模型,分别开展该机匣在不工作状态下的模态分析。
由于二维传统轴对称模型无法获得机匣的弯曲模态,因此本小节重点对比三维实体和二维傅里叶轴对称模型的振动结果,如图8和表5所示。
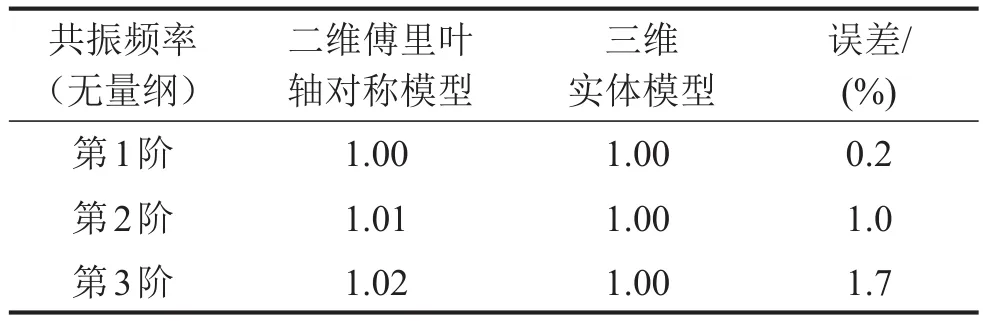
表5 机匣共振频率计算结果(以三维模型的共振频率为基准进行归一化)
由以上分析可知,分别基于三维实体和二维傅里叶轴对称模型计算获得的对开机匣共振频率接近,最多相差1.9%;两者的模态位移分布也一致;此外基于二维傅里叶轴对称模型可以获得机匣的弯曲模态,这是二维传统轴对称模型无法做到的。
这表明可以通过在二维傅里叶单元周向展开截面上设置轴向加强筋来模拟纵向安装边,继而考察机匣的共振问题。另外两种分析模态在振动计算耗时对比如表6所示,可见二维傅里叶轴对称模型可以大大降低计算规模,提高分析效率。
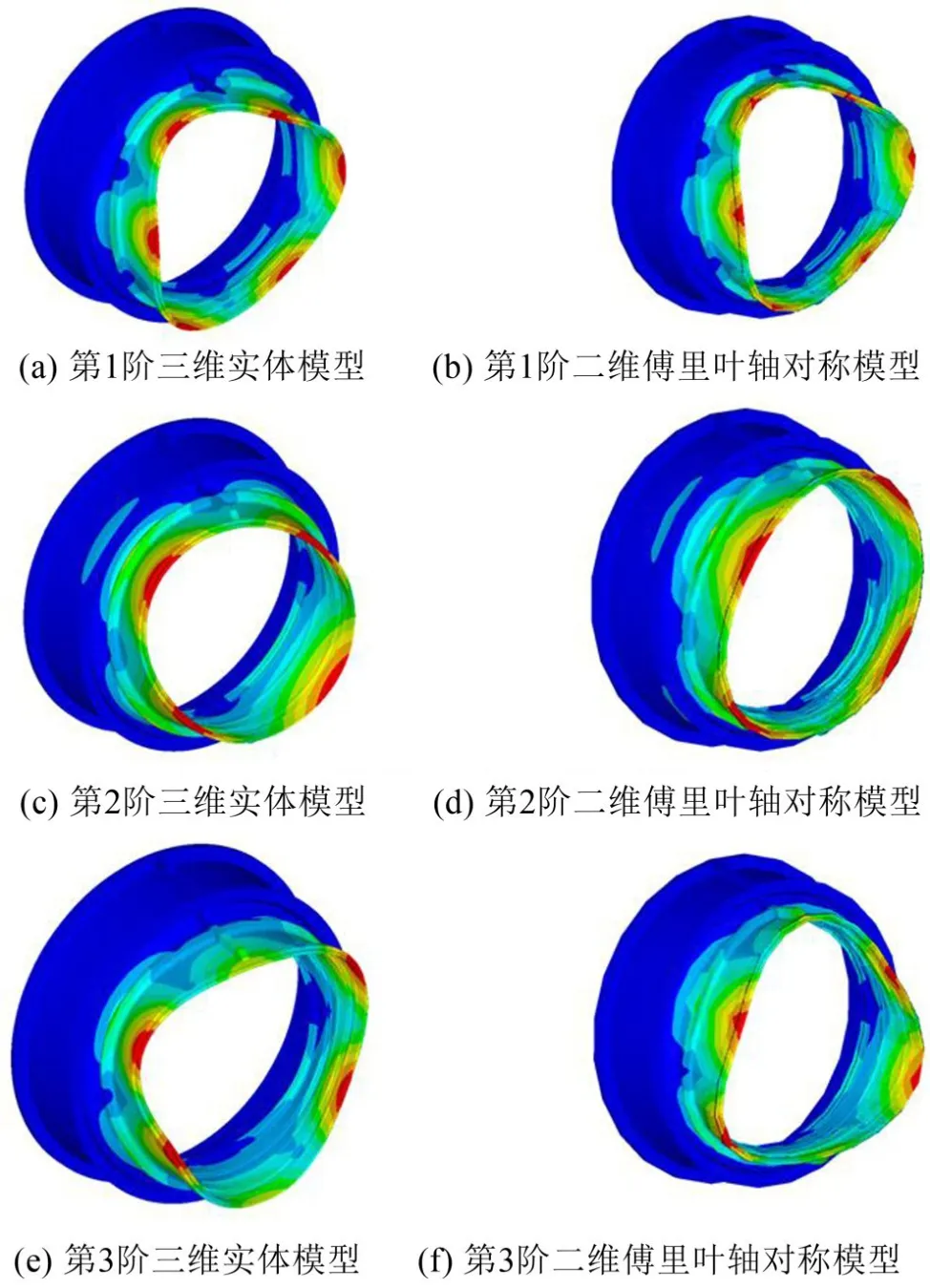
图8 对开机匣前3阶共振模态

表62 种分析模型的模态计算耗时对比/min
3 结语
基于某型航空发动机高压压气机延伸对开机匣,通过在二维傅里叶单元周向展开截面上设置轴向加强筋来模拟纵向安装边,继而对其机匣应力、变形沿周向的不均匀度和振动进行了分析,并与二维传统轴对称模型和三维实体模型的计算结果进行了对比,可知:
(1)基于二维傅里叶轴对称模型计算得到的机匣应力分布,与对应三维实体模型的应力分布大致一致,可以用于评估由于纵向螺栓安装边等非轴对称特征带来的机匣应力沿周向的不均匀问题,且应力结果略显保守;
(2)基于二维傅里叶轴对称模型计算得到的机匣变形沿周向的不均匀度和振动结果,与对应三维实体模型分析结果一致,且差别很小,可以用于评估机匣变形椭圆度对气动性能的影响和用于计算机匣振动;
(3)二维傅里叶轴对称模型的计算规模和耗时远远低于三维实体模型,具有良好的计算效率。
因此可以通过在二维傅里叶单元周向展开截面上设置轴向加强筋来模拟纵向安装边,继而考察此类具有旋转轴对称特征但局部存在非轴对称特征(如纵向螺栓安装边)机匣应力、变形沿周向不均匀度和振动问题,具有良好的计算精度和分析效率。
