金属O形环力学性能仿真分析与试验验证
2019-08-27张文昌励行根2魏世军2贾晓红
张文昌 励行根2 魏世军2 贾晓红 郭 飞
(1.清华大学摩擦学国家重点实验室 北京 100084;2.宁波天生密封件有限公司 浙江宁波 315302)
金属O形环(以下简称O形环)是核反应堆压力容器中常用的密封,具有大接触应力、耐高温、耐腐蚀等优点。O形环密封系统主要由封头或上法兰、筒体端部或下法兰、O形环及其他必要的紧固件组成。O形环一般采用金属圆管弯制焊成,常在外表面涂或镀银等塑性较好的材料以提高密封性能。
O形环自身的力学性能对其密封性能影响显著。密封环通过形变,增加工质在密封界面的流动阻力从而形成密封。受到轴向载荷时O形环的压缩特性反映了密封环表面与法兰表面形成初始密封的能力。而当密封系统在实际工况下,由于螺栓及法兰的形变,使得法兰接触面与O形环接触面产生了相对分离的趋势。此时O形环的回弹能力对于该密封系统连接的紧固程度有较大的影响[1]。
通过研究O形环的力学性能可以为其产品设计和改进、质量监督、密封性能监控等工作提供依据。自1960年美国首次将空心金属O形环应用于反应堆始,各国研究者陆续针对O形环密封特性[2]、形变特性[3]、截面结构[4]以及材料的超塑性[5]、低温高周疲劳性能[6]、长时间组织稳定性[7]等开展了大量研究,同时总结了大量经验设计方法并开展了相关仿真分析方法研究[8-11]。但主要研究成果集中于O形环的压缩回弹特性的试验和经验模型。
本文作者旨在以核反应堆压力容器用金属O形环为研究对象,考虑密封环的复合结构、材料弹塑性特征和工况条件,采用有限元方法建立O形环力学性能仿真模型,分析密封环的压缩回弹特性、应力应变特征、接触特性以及银层的作用,并进行相关试验验证。
1 有限元模型和试验方法
压力容器中采用了双道O形环,由于内侧与外侧O形环力学特性相同,在此只选取内侧O形环进行建模。O形环主体部分是φ12.7 mm×1.27 mm的空心环,由Inconel 718合金管材无缝焊接而成,表面镀有厚度为0.15~0.22 mm的银层。
O形环的力学仿真涉及材料弹塑性、密封圈结构大变形以及接触非线性,根据O形环结构和受力特点,建立如图1所示的平面二维轴对称模型以提高计算效率。
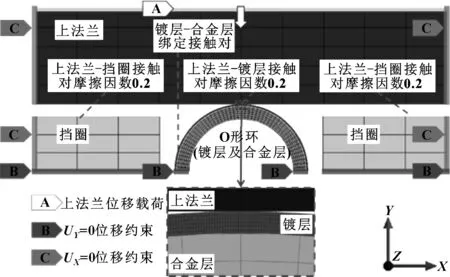
图1 金属O形环密封系统的有限元模型
上下法兰为线弹性不锈钢材料,O形环Inconel718合金及银层采用多线性等向强化(MISO)材料模型。几何模型绕轴线(Y轴)为对称轴,施加对称约束条件,上法兰与挡圈施加UX=0位移,在上法兰施加Y向位移载荷。取最大压缩量为2.4 mm,由于上下法兰对称性,上法兰压缩量为1.2 mm;卸载时,将原施加UY=-1.2 mm载荷逐渐减小,直至O形环与法兰脱离,模拟密封系统使用过程容器内充气、 容器内压的变化等因素引起的法兰分离。加卸载过程为准静态。
压缩回弹特性测量试验在图2所示的垫片综合性能试验机上进行,包括液压机(YJN-100)、位移传感器NS-WY02-20-5(精度:0.05%)、力传感器BLR-1(灵敏度:1 mV/V)。参照GB/T 12622中垫片压缩回弹特性的测量方法,在室温20 ℃环境下以0.5 MPa/s的速率加载卸载,测量垫片的应力与变形关系。由于仿真环和实验环直径不同,采用线比压进行比较,如图3(a)所示。

图2 垫片综合性能试验机示意图
2 力学特性结果分析
2.1 压缩回弹特性
O形环的压缩回弹特性反映了预紧状态下初始密封的形成能力和操作工况下密封的保持能力和裕量,是衡量O形环力学性能的主要指标。O形环的轴向载荷F-压缩率η曲线反映了O形环的压缩回弹特性,图3(b)给出了F-η压缩回弹曲线。
图3(b)所示曲线包括了弹性变形区、塑性变形区和法兰接触区,仿真计算和试验测量的各段区域分界点和变化趋势具有很好的一致性。以最大压缩率
为18.5%时的O形环压缩回弹特性曲线为例。加载过程可以分为3个区域:(1)加载初期,载荷随压缩率呈线性增长趋势,此时为弹性变形区;(2)加载中期,当压缩率达到2%附近时,开始进入塑性变形区,O形环镀层与合金层作为整体,其整体刚度降低;(3)加载后期,上下法兰发生接触后继续加载,进入法兰接触区,由于法兰刚度较大,轴向载荷突然增大,且与压缩率呈线性关系陡增,当达到最大压缩率18.5%时轴向载荷已经达到105kN量级。
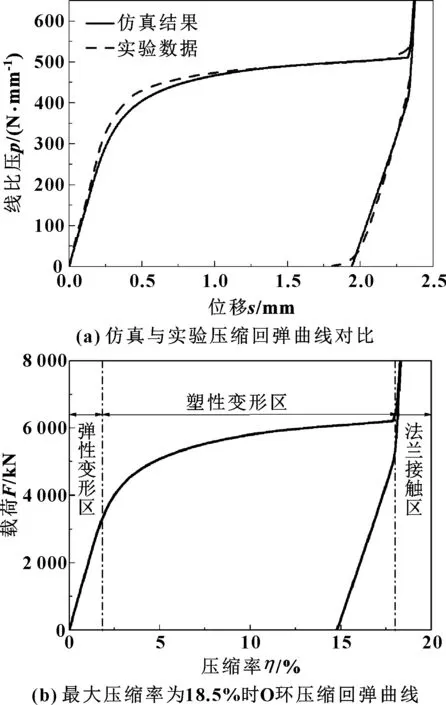
图3 仿真与试验结果对比及O形环压缩回弹曲线
卸载过程,由于法兰处于弹性变形范围,因此加载卸载曲线均与压缩率呈近似线性关系;持续卸载O形环进入塑性变形区后,O形环的塑性形变保留,弹性形变开始恢复,O形环产生回弹,最终完全卸载后仍然有部分残余形变。不同曲线在加载段几乎重合,卸载段卸载起点不同,但卸载段除进入法兰接触区的部分受到刚性较大的法兰的影响,其余卸载段曲线基本互相平行。
2.2 接触特性
图4给出了加载过程中O形环和上法兰接触压力的变化规律,取压缩率分别为0、1%、3%、7%、10%,以及完全加载即压缩率为18.5%,作出接触压力曲线。横轴为有限元模型中的X坐标,零点表示O形环原始外径最高点,即与法兰的切点。
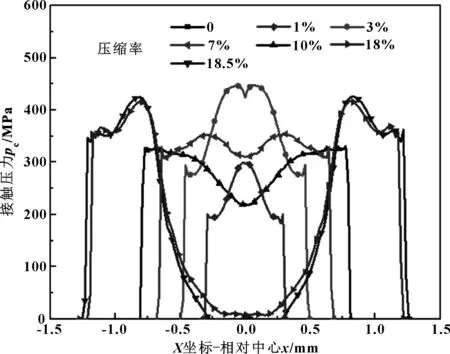
图4 加载过程接触压力变化
O形环经过有限元离散化处理并非严格的圆形,法兰和O形环初始相切的位置,也有很小的接触压力,这属于离散化带来的误差。因为数值很小,所以可以忽略不计。当压缩率较小(载荷较小)时,O形环径向最高点与法兰接触,接触压力分布近似为倒U形;随着载荷增大,接触宽度和接触压力都随之增大。当压缩率达到约3%时,接触宽度进一步增大,但是接触压力则有所减小,尤其接触区中间压力更小,出现内凹。随着压缩率进一步增加,接触区宽度增大,最大接触压力减小,接触压力内凹程度也继续增大。当压缩率达到17.8%时,法兰和挡环开始接触。可以看出,当法兰和挡环开始接触后,O形环与法兰的接触区中间部分近似脱离接触,接触区中间开始凹陷,在凹陷区两侧出现对称的2个接触区;随着压缩率的增大,O形环与法兰之间的接触压力基本不变,增大的载荷由挡环承担,所以挡环与法兰之间的压力随载荷增大而增大。
接触宽度在加载和卸载过程中也因塑性变形而变化。分析接触宽度的变化会发现其与图3所示的压缩回弹特性曲线具有相同的特征。
2.3 应力应变特征
图5所示为等效弹性应变最大值、等效塑性应变最大值及等效应变最大值随压缩率变化的曲线。
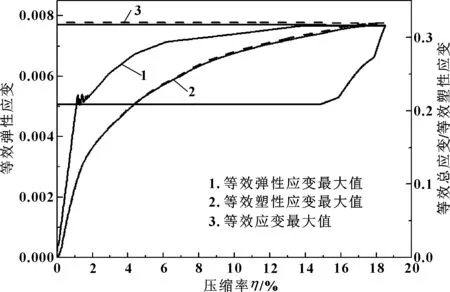
图5 O形环等效应变最大值变化
可以看出弹性应变在加载初期较快地接近其最大值,在压缩率为0~1%之间,弹性应变最大值呈线性增长,压缩率达到1%附近后其最大弹性应变达到0.005即其屈服极限,应变值上下抖动,材料开始发生塑性变形,进入流动阶段;继续增加压缩率,O形环进入强化阶段,材料恢复了对变形的抵抗能力。卸载时由于O形环发生了塑性形变,因此塑性应变最大值保持不减,卸载阶段弹性应变最大值随卸载而减小,但并未完全消失,而是由于各部分变形量不同,回弹过程中各部分要恢复的弹性变形不同,各部分之间为了变形协调就会产生一定的相互约束,导致了在完全卸载后仍然留下一定的残余应变。
图6给出了O形环完全加载时各节点的位移矢量。可以看出:O形环中心部分节点以Y轴位移为主,左侧部分节点以X轴位移为主,且径向位移小于轴向位移。位移矢量长度最小节点约处在截面40°处,其位移矢量方向基本与初始轮廓相切。
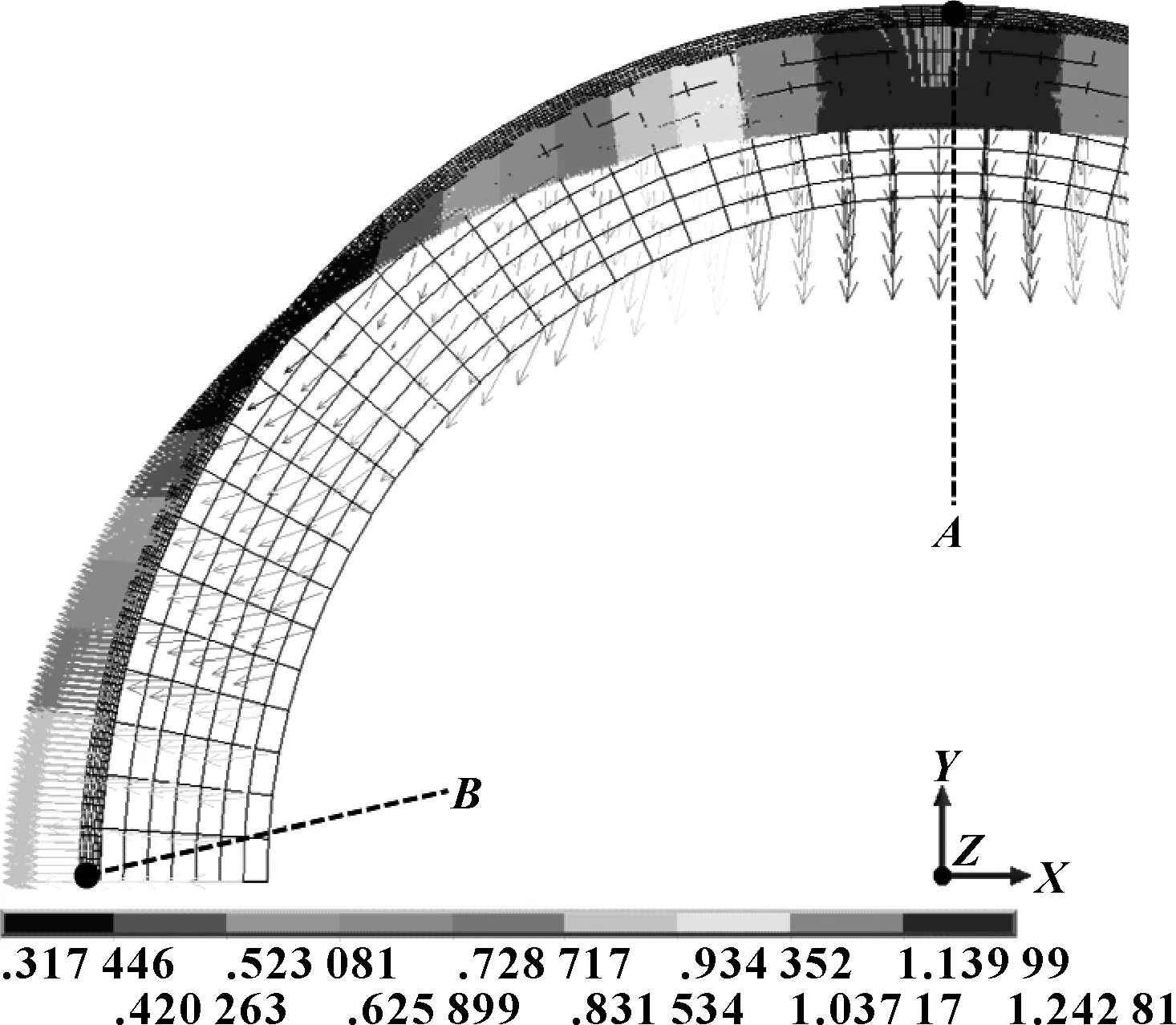
图6 完全加载各节点位移矢量
3 镀银层影响分析
镀层的存在及其厚度是影响O形环力学特征的一个因素,图7给出了3种镀层状态及不同镀层厚度下O形环的压缩回弹曲线。3种状态分别为:(1)公称尺寸状态,即存在镀层,外径d=13 mm,镀层厚度γ=0.15 mm;(2)无镀层状态,即仅存在合金层,O形环外径d=12.7 mm;(3)加厚合金层状态,即仅存在合金层,但O形环外径与状态(1)保持相同,d=13 mm。
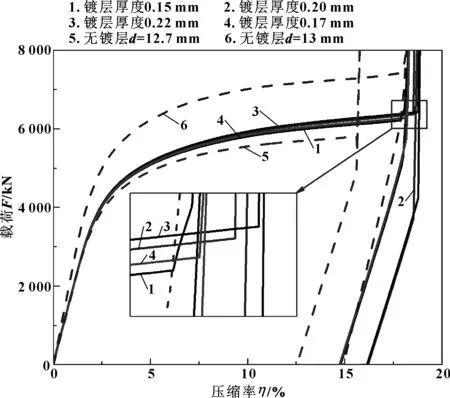
图7 不同镀层压缩回弹特性曲线
比较状态(1)与状态(2),在加载阶段,二者压缩回弹曲线非常接近,失去银层的O形环在相同压缩率下由于外径减小,因此上法兰位移更大,上下法兰更早接触,压缩回弹曲线更早进入法兰接触区。因此,O形环的结构刚度主要取决于合金层,相同的合金层厚度下,镀层有无对压缩回弹曲线的总体趋势影响不大。同时比较状态(1)与状态(3)也可以看出同样规律。
图8中比较的是状态(1)与状态(3)不同压缩率下对应的接触压力分布。可以发现状态(1)与状态(3)各自接触压力分布随压缩率的变化趋势相同,状态(1)与状态(3)具有相似的接触压力分布变化规律,镀银层对该规律基本无影响。但是在相同压缩率下,无镀银层的O形环其接触压力峰值更高,接触压力分布在峰值附近更为集中。这是因为镀银层材料较合金层更易发生形变,材料塑性更好,对于接触压力的分布起到了均化的作用,增大了接触宽度,更好地填补了泄漏通道,利于形成密封。

图8 有无镀层O形环加载时接触压力分布(外径d=13 mm)
4 结论
(1)建立金属O形环的平面二维轴对称有限元模型,仿真得到的压缩回弹特性与试验结果具有良好一致性,表明该有限元模型可用于O形环力学性能的分析。
(2)利用该有限元模型进行了O形环力学性能的分析,包括接触特性、应变特性及压缩回弹特性。分析结果表明:O形环接触压力分布与压缩率有关,压缩率过大或过小都将导致密封性能下降;整个压缩回弹过程可分为弹性变形、塑性变形、法兰接触及回弹4个阶段,O形环的回弹补偿性能由其压缩率决定。
(3)讨论了O形环表面镀银层对于其力学特性的影响,表明镀银层主要对O形环密封的接触压力分布起均化作用,而对O形环总体的压缩回弹特性影响不大。
(4)建立的模型和分析方法可用于其他法兰垫片密封系统的力学特性研究。
