压裂封隔器密封系统流体穿透仿真研究*
2019-08-27
(1.西南石油大学机电工程学院 四川成都 610500;2.四川宝石机械专用车有限公司 四川德阳 618300)
压裂封隔器是多段压裂技术中的核心工具之一[1-2],其工作原理是通过坐封压力使得胶筒轴向压缩,使径向半径增大并与井壁接触形成密封,将井眼分隔从而实现分段压裂作业[3]。因此,胶筒的密封能力是决定压裂封隔器密封性能的关键。
近年来,研究人员从增强封隔器密封性能角度出发,已经开展了大量的研究。伍开松等[4]研究了封隔器胶筒密封几何参数的优选,分析了接触应力随胶筒高度、厚度、倒角等参数的变化规律。张付英和姜向敏[5]利用应力-强度干涉理论建立了胶筒密封的可靠性模型,得出了影响胶筒密封可靠性的主要参数及参数变化的灵敏度。王鹏[6]考虑高温高压完井封隔器中锁紧机构和中心管的力学关系,对封隔器整体进行力学仿真分析,得到封隔器工作时各部件三维应力关系。张付英等[7]研究了胶筒与套管之间的接触应力及沿轴向的分布规律,以及施加不同扭转载荷时对胶筒密封性能的影响。谢代培[8]从工艺管柱、工具质量、作业质量、测试工艺、生产管理等方面,对封隔器密封率的影响进行了分析总结,并提出了相应的对策。张峰[9]揭示了胶筒坐封力加载方式对密封性能的影响规律,为新型封隔器的研制提供了理论依据。李斌等人[10]将等直径的胶筒组设计为变径鼓形胶筒,并研究了变径鼓形胶筒和套管间的接触应力大小与分布规律。但上述研究对封隔器的泄漏原因和泄漏过程却鲜有提及。
封隔器的密封属于静密封的一种。静密封泄漏的成因,研究人员认为是密封接触面存在泄漏通道[11-14],高压端流体通过泄漏通道进入低压端,并推导了相应的泄漏量计算方程。但上述研究未考虑高温对橡胶力学性能的影响,且忽略了流体与胶筒会互相影响产生变形,因此用这样的理论描述封隔器的泄漏现象并不完善。当封隔器坐封成功后,由于胶筒与井壁表面凹凸不平,密封时存在微小泄漏间隙[15-16],而原油、天然气、钻井液等介质在足够大的压差下,会通过挤压密封面端面间隙、扩张端面间隙并通过胶筒变形进一步扩大间隙形成泄漏,造成封隔器胶筒的密封失效。整个泄漏过程中,胶筒在流体介质的载荷作用下产生变形,而胶筒的变形又会导致流体载荷大小与分布的变化。因此,本文作者为研究封隔器胶筒密封的失效本质,建立了封隔器流体穿透模型,采用浸入边界法,模拟高压流体穿透封隔器导致封隔器密封失效的整个过程,并通过高温高压胶筒泄漏试验来验证该过程的正确性与准确性。文中从动态的角度来研究封隔器胶筒的密封失效本质,为封隔器的设计和研发提供了参考。
1 高温下橡胶力学性能试验
封隔器胶筒主要采用橡胶材料,而橡胶材料具有强烈的非线性特征,受温度影响大。因此采用高温下的单轴拉伸试验来测定橡胶试样的应力-应变曲线。如图1(a)所示为橡胶试样,图1(b)所示为120 ℃下,橡胶试样的单轴拉伸试验。

图1 橡胶试样(a)和高温单轴拉伸试验(b)
应变能函数常用于描述橡胶材料的力学性能,根据试验测得应力-应变数据,拟合Mooney-Rivlin模型用于描述橡胶密封单元的大变形行为。假设橡胶材料为各向同性材料,且不考虑材料力学行为的时间相关性,即应力松弛、蠕变和老化等现象,则应变能密度函数W[17]为
(1)
其中
(2)
(3)
(4)
式中:λ1,2,3是3个主伸长比。
则有Mooney-Rivlin模型[18]为
W=C10(I1-3)+C01(I2-3)
(5)
如图2所示,根据单轴拉伸试验所获得的应力-应变数据拟合Mooney-Rivlin本构模型,得到的C10=-0.38 MPa,C01=1.80 MPa。
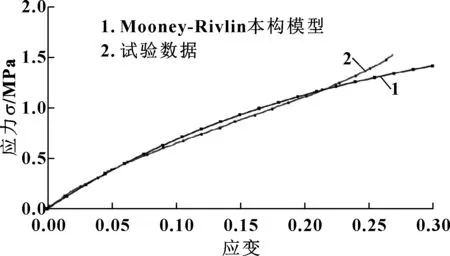
图2 单轴拉伸试验数据与Mooney-Rivlin本构模型拟合曲线
2 封隔器流体穿透模型与前处理
2.1 建立简化的封隔器密封系统流体穿透模型
以Y344型压裂封隔器为研究对象,其具有4组密封胶筒和4组端部胶筒,端部胶筒主要起保护作用。密封胶筒最高密封压差能达到70 MPa,胶筒材料为氢化丁腈橡胶,井下工作温度为120 ℃。文中以胶筒的密封性能为主要研究目的,为提高计算效率,在建立模型时对模型进行简化,并且在网格划分时,对胶筒网格进行细化以提高计算精度。如图3所示为简化的封隔器密封结构二维模型。
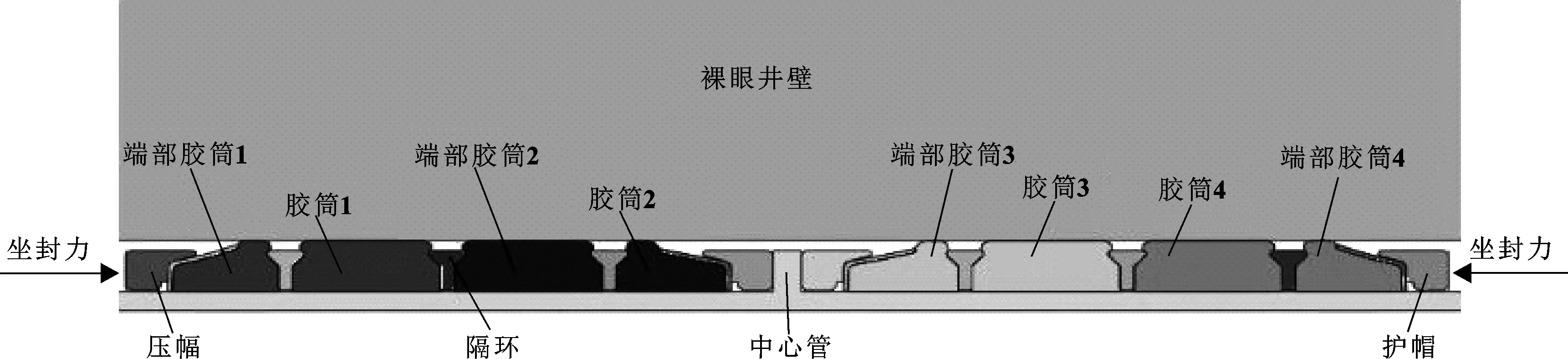
图3 简化的封隔器二维模型
2.2 网格划分
为了获得高质量的网格,利用封隔器密封结构二维模型,通过切分的方法将各部件分割成形状规则的几何形状,然后通过曲面旋转、扫略的方法来生成胶筒、端部胶筒、压帽、护帽、隔环和井筒三维模型。根据封隔器内流体可能流动的区域建立流体模型为160 mm×160 mm×340 mm(长×宽×高)的长方体。对封隔器密封结构采用六面体单元划分,井筒共6 000个单元,隔环和压帽共130 600个单元,护帽共87 040个单元。胶筒和端部胶筒共51 600个单元,中心管共4 000个单元,如图4(a)所示为整体网格模型,如图4(b)所示为胶筒网格模型。

图4 整体网格模型和胶筒网格模型
流体域为长方体,需将封隔器密封结构流体通道包络起来,流体域共450万个欧拉单元。流体欧拉单元必须与坐标轴平行,以达到利用快速耦合技术实现加快求解计算速度的目的。
2.3 材料属性
封隔器密封系统流体穿透过程数值模拟计算的主要目的是为了获得流体压力作用下胶筒和端部胶筒密封状态的变化,为了减小计算规模,不考虑井筒和中心管的变形,井筒和中心管均设定为刚体;压帽、护帽和隔环采用变形体。计算采用的流体介质设定为清水,如表1所示。

表1 流体性质参数
2.4 载荷与边界
首先对模型上端的压帽施加轴向压力,达到坐封的效果,坐封状态稳定后从下端通入流体。为模拟橡胶受到液体压力逐渐撑开的过程,入口流速是一个逐渐增大的渐变过程,出口定义为任意出流。井筒和中心管圆柱面约束所有自由度,确保在流体作用下不会发生任何运动,胶筒、端部胶筒、压帽、护帽和隔环不进行任何约束,如图5所示为模型载荷与边界条件示意图。

图5 模型载荷与边界条件示意图
3 数值模拟
3.1 浸入边界法
PESKIN[19]在1972年提出了浸入边界法的思想,首先利用Navier-Stokes动量方程的附加力项把复杂结构的轮廓边界模糊化,然后将Navier-Stokes动量方程的附加力施加在流体边界的网格模型节点上,通过上述方法能够很容易地模拟出复杂的边界形状。如图6所示为浸入边界法示意图,浸入边界法在数学方法上采用欧拉变量表述流体,采用拉格朗日变量表述拉格朗日固体结构边界,利用近似函数、固体和流体的相互作用通过分布的节点力和速度差值实现[20]。
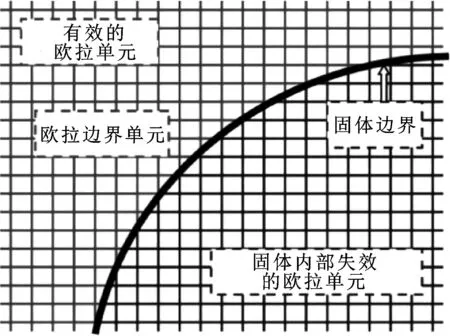
图6 浸入边界法示意图
在封隔器坐封完成后,胶筒与裸眼井壁或套管之间紧密贴合,无流体介质存在,因此贴体非均匀网格重构法不适合解决封隔器密封系统流体穿透问题。而浸入边界法克服了贴体非均匀网格重构法需要流体域始终存在的缺点,适合解决封隔器密封系统流体穿透问题。
3.2 封隔器坐封
封隔器胶筒的大变形特征和运动规律直接体现了封隔器的坐封和液压撑开的过程,为数值仿真的核心。在坐封过程中,胶筒、端部胶筒的轴向、径向变形是非均匀的,尤其径向膨胀沿轴向变化;井壁、中心管和胶筒之间的挤压力、摩擦力沿轴向均不相同,需要通过耦合计算才能得到其协调变化规律;同时,胶筒、隔环、护帽端面形成了一种接触区域持续变化的非线性边界条件,在高压流体的推动下,各胶筒、端部胶筒沿轴向的滑移是不相同的。
选取Y-Z截面观察封隔器密封系统流体穿透仿真计算结果,在0~0.002 5 s完成封隔器坐封。从图7中不难看出,随着上端压帽受压下移,护帽与压帽完全接触,并继续下行压迫端部胶筒。护帽与端部胶筒在坐封压力下均产生明显的变形,胶筒、端部胶筒在轴向的挤压下沿径向扩展与井壁形成接触。
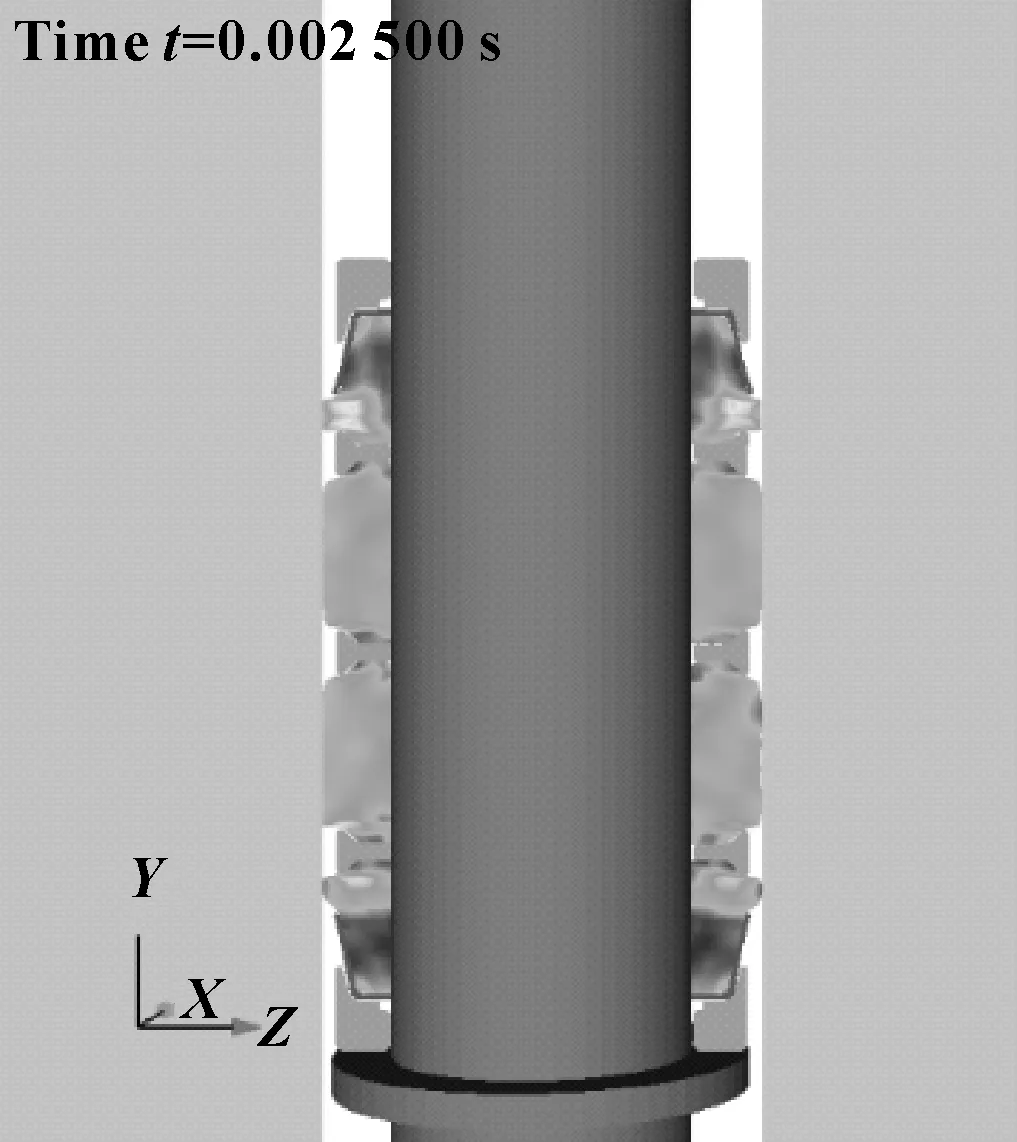
图7 封隔器坐封状态
3.3 临界液压值
选取X-Z截面观察流体压力,并绘制Y-Z截面流体矢量图。坐封成功后,从下端注入液压,如图8所示,在0.003 6 s时,流体即将冲破端部胶筒密封,撑开端部胶筒。从X-Z平面压力云图中可见井壁内侧形成高压,最大压力为20 MPa,这说明当流体压力达到20 MPa临界值的时候,封隔器橡胶将开始被穿透,密封效果遭到破坏。

图8 端部胶筒临界液压
3.4 密封失效
图9所示是液压不断增大,流体流入端部胶筒、胶筒示意图,可以看出计算实现了端部胶筒、胶筒的压缩变形和在流体驱动下的位移变化,而端部胶筒、胶筒位置的变化影响到了流域的变化,实现了封隔器密封系统流体穿透过程计算模拟。随着流体的不断浸入,端部胶筒、胶筒被逐渐撑开,沿径向受到压缩,胶筒密封最终失效。

图9 流体浸入过程示意图
在Y-Z平面的端部胶筒、胶筒内外侧各取4个参考点(参考点具体位置如图10所示),以观察随时间变化各点沿Z向和Y向的位移情况,即橡胶整个过程沿横向和径向的位置变化。结果如图11、12所示。
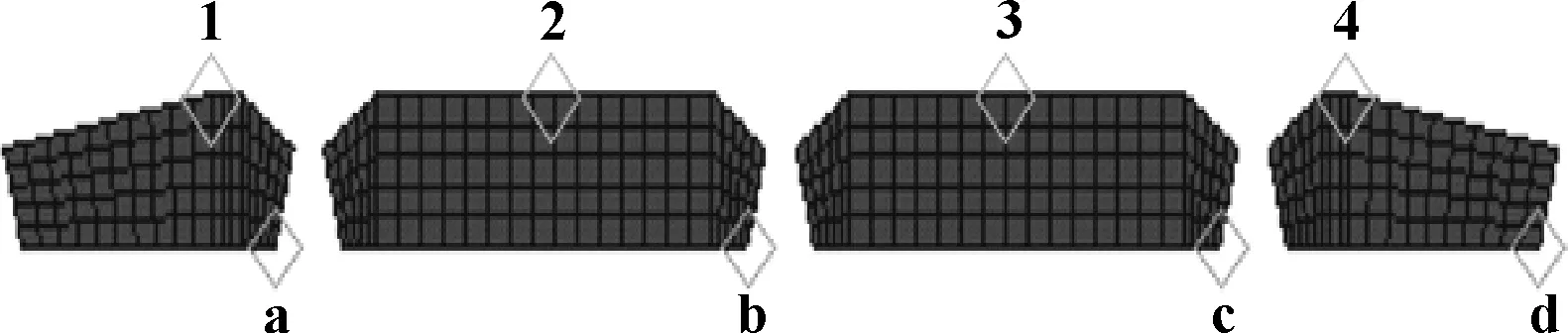
图10 胶筒参考点选取
从图11可看出,参考点1(最下端端部胶筒)初始位移是0,随时间变化,先是沿Z轴负向移动到-5 mm,橡胶形成坐封,达到相对稳定状态后被流体浸入,参考点沿着Z轴正方向移动,0.006 s时Z向位移是2.25 mm。而从参考点2、3、4的位移变化可以看出,靠近上端的参考点4最先受到坐封压力作用沿径向-Z向移动,由于参考点3和参考点4远离流体入口,因而尚未被流体穿透;最靠近下端的参考点1和2较晚受到坐封影响沿-Z方向移动,但距离流体入口比较近,在0.006 s时就已经被穿透。在流体作用下各点沿Z向位移呈现波动性的变化。
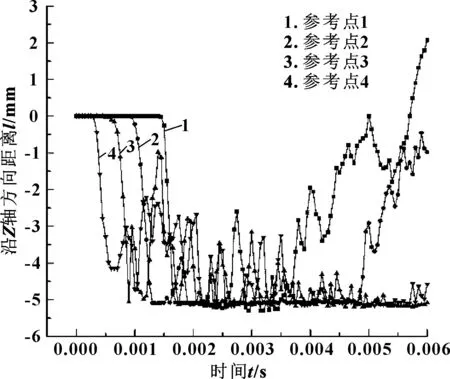
图11 胶筒外径各参考点Z向位移分布曲线
从图12中所示的a、b、c、d 4个参考点Y向位移可以看出,参考点a、b、c、d四点分别在0.000 1、0.000 3、0.000 9、0.001 45 s时开始沿Y负方向移动;到0.002 s时向下压缩停止,此时各点Y向位移不再明显变化,表示胶筒坐封完成;在0.002 2 s时开始从底部通入流体;到0.002 3 s时,4个观察点均开始向Y正方向移动;随着流体不断浸入参考点a、b、c呈波动状态,在0.004 s后波动状态不再出现,参考点逐渐向Y正向移动。
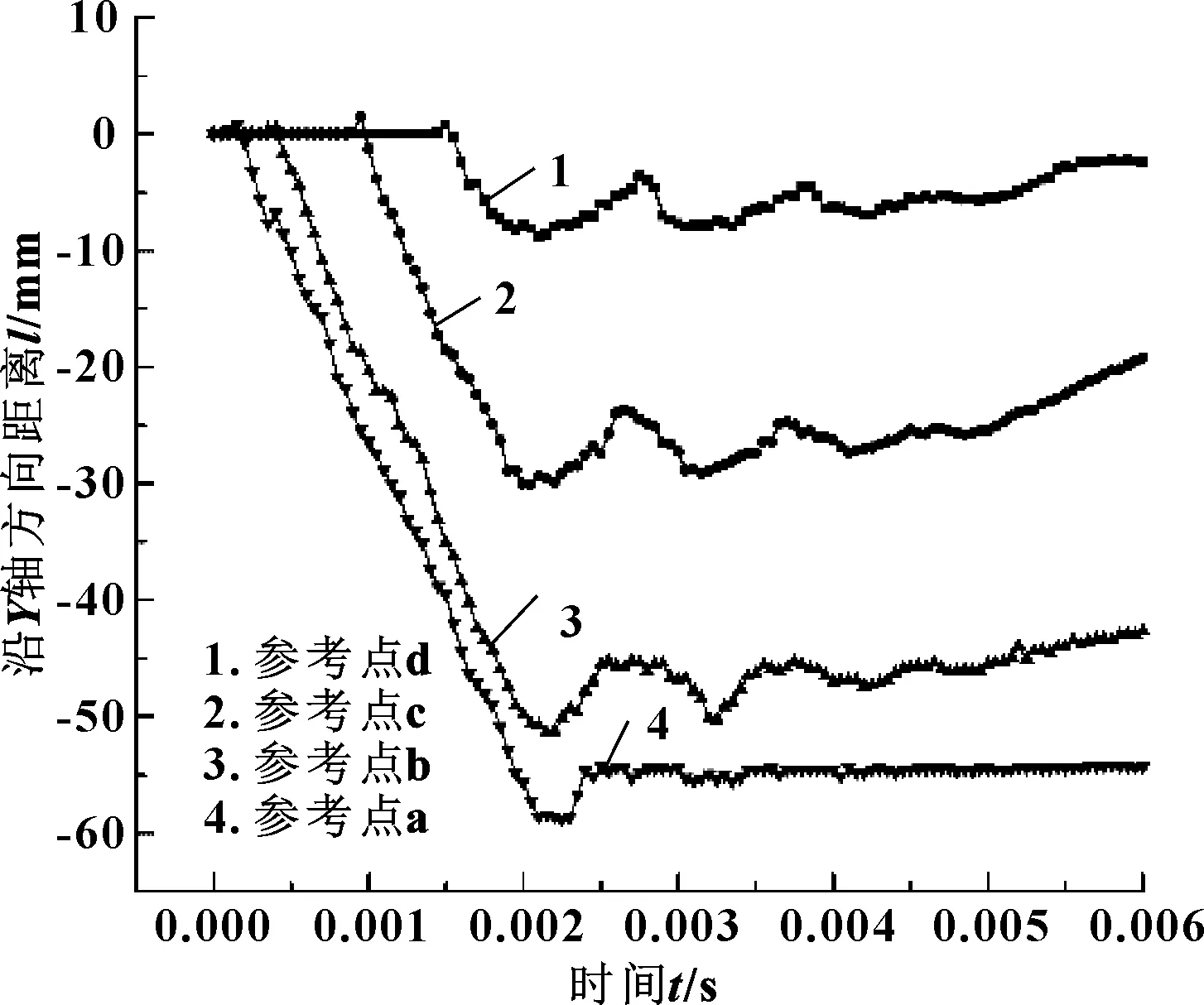
图12 胶筒内径各参考点Y向位移分布曲线
从图13中可以看出,参考点1在0.006 s时流体压力为55.01 MPa,而参考点2在0.006 s时流体压力为77.70 MPa。从图12中可知,在0.006 s时,参考点1、2的Z向位移逐渐减小,即胶筒密封已经失效,而参考点3和4的Z向位移几乎没有变化,因此在0.006 s时,第一个端部胶筒和第一个密封胶筒密封已经失效,该状态对应的流体压力为77.70 MPa。而随着时间和压力的继续增加,参考点处的流体压力也会持续增加,直至所有的胶筒都被穿透。

图13 参考点1和参考点2流体压力变化情况
4 封隔器胶筒泄漏试验
如图14所示,为封隔器高温试验井系统结构示意图,该试验井系统主要由控制系统和高温试验井两部分构成。在试验时,将封隔器胶筒加热至120 ℃,打下压坐封,上下压差至为70 MPa,稳压15 min以上,根据API 11D1[21]中封隔器胶筒密封性能接受标准,若稳压期间压降不超过1%,则胶筒密封性能合格。

图14 封隔器高温高压试验井结构示意图
如图15所示为Y344型压裂封隔器胶筒在高温高压下的泄漏试验。试验开始时前10 min对胶筒进行预热至工作温度120 ℃,并进行坐封;从第10 min开始对胶筒进行缓慢加压,加压至70 MPa并稳压25 min后测试胶筒的密封性能;继续缓慢加压,当加压至78 min时,压力下降,且压降超过1%,认为胶筒已经出现泄漏,终止试验。测得在77 min左右胶筒的临界压力为82.39 MPa。
试验测得的封隔器胶筒泄漏临界液压值82.39 MPa,与仿真得到的临界液压值77.70 MPa之间误差值不超过10%,证明了流体穿透封隔器过程的有效性与正确性。图16所示为胶筒在泄漏试验前后对比。
根据试验过程和试验结果可知,加压至40 min左右时,密封胶筒上下压差为70 MPa,稳压25 min,压差几乎不产生变化,表明该密封胶筒在高温下的确能密封70 MPa的压差,胶筒质量合格。而后续持续加压至78 min时,压力突然下降,原因在于过大的压力穿透了密封面,形成了泄漏通道,导致胶筒上下两端压差下降。而试验结果与仿真结果基本一致,验证了仿真的正确性。
5 结论
(1)通过对封隔器胶筒泄漏过程的仿真可以知道:流体在压力不断增加时,会不断浸入密封间隙、挤压间隙,而由于胶筒橡胶是大变形材料,在高压流体的挤压作用下,产生轴向和径向的压缩,导致胶筒与井壁接触面分离,而流体继续填充,最终间隙会不断增大,而流体也会穿透胶筒与井壁的接触面形成泄漏通道,并不断扩大泄漏通道增加泄漏量。
(2)在穿透过程中因为胶筒与流体互相影响,因此压力不断波动,在流体穿透胶筒的瞬间,有临界液压值,而后因为胶筒与胶筒之间还存在空间,因此流体压力会出现下降。
(3)研究的Y344型压裂封隔器胶筒,在流体压力为20 MPa时,下端端部胶筒被穿透,而在流体压力为77.70 MPa时,第一个密封胶筒被穿透,胶筒密封失效。该胶筒的高温高压试验结果表明,胶筒在82.39 MPa时会产生泄漏,试验结果与仿真结果误差不超过10%,证明了模拟的流体穿透封隔器过程是准确的。而后续流体压力不断增加到某一阀值时会导致所有胶筒被穿透,封隔器胶筒密封失效。
