基于Hamilton理论的无人车路径跟踪控制
2019-08-27陈特陈龙徐兴蔡英凤江浩斌
陈特, 陈龙,2, 徐兴,2, 蔡英凤,2, 江浩斌,2
(1.江苏大学 汽车与交通工程学院,江苏,镇江 212013;2.江苏大学 汽车工程研究院,江苏,镇江 212013)
近年来,智能汽车技术发展迅速并得到了整个汽车行业乃至相关交叉性领域研究人员前所未有的关注,其中L3级别的车辆自动驾驶技术是当前行业研究的热点[1-3]. 无人车辆路径跟踪控制是车辆智能化发展方向的重要研究问题之一,目前已有许多研究成果[4-6]. Leng等[7]和李培新等[8]利用前馈控制与反馈控制结合的方式,同时考虑了转向约束问题,研究了拖车的路径跟踪控制方法.
在现有的研究文献中,通常采用模型预测控制、鲁棒控制、滑模控制及其结合的方式设计路径跟踪控制器. Kim等[9]结合车辆转向系统动力学特性,基于模型预测控制算法提高了车辆路径跟踪性能. Wang等[10]和Hu等[11]基于鲁棒H∞控制和滑模控制理论,同时考虑了时滞、数据溢出以及模型不确定性等因素,研究了相应控制理论的车辆路径跟踪应用及控制算法的车辆表现. 同时,一些文献研究了多执行结构耦合条件下的车辆稳定性与路径跟踪集成控制问题,利用子系统的耦合关系,实现了多控制目标下车辆控制需求的协调. Ni等[12]针对四轮独立驱动无人车,设计了纵向、横向以及横摆控制器,并通过转向以及轮胎力分配实现控制需求,设计了一种路径跟踪与车辆稳定的集成控制策略. 四轮驱动四轮转向汽车相比传统汽车具有更高的控制自由度[13-15],在该汽车平台上研究无人车辆路径跟踪问题,将有助于进一步提高车辆路径跟踪效果.
文中针对四轮驱动四轮转向无人车路径跟踪问题,提出了一种基于Hamilton理论的无人车路径跟踪分层控制策略. 在上层控制器中,利用Hamilton理论实现车辆路径跟踪误差模型的自我镇定,同时在下层控制器中,利用4个车轮纵向的优化分配实现车辆上层控制需求,以期减小车辆路径跟踪过程中的横向误差和航向误差.
1 无人车辆系统建模
1.1 车辆动力学模型
如图1所示,将动态坐标系xOy固定于车辆重心位置,其中x轴正方向与车辆纵向运动方向重合,y轴沿着车辆横向且从右至左为正方向,不考虑车辆的侧倾、俯仰以及垂向运动,假定4个轮胎的机械特性一致,编号1,2,3,4分别代表右前、左前、左后以及右后轮,从而建立车辆的二自由度模型,用来表征横向以及横摆方向的车辆运动特征. 二自由度车辆模型动力学方程为
(1)
(2)

图1 二自由度车辆模型Fig.1 Vehicle model with 2 degree of freedom
式中:vx为纵向车速;vy为侧向车速;γv为横摆角速度;m为汽车质量;Iz为绕z轴的转动惯量;Fyf和Fyr分别为前后横向轮胎力;δ为前轮转角;lf为质心距前轴的距离;lr为质心距后轴的距离;ΔMz为由4个轮胎纵向力所产生的车辆横摆力矩
(3)
式中:bs为前后轴的半轮距;Fxi(i=1,2,3,4) 为第i个轮胎的纵向力. 横向轮胎力可表示为
(4)
式中:Cf和Cr分别为前后轮胎侧偏刚度;αf和αr为前后轮胎侧偏角. 轮胎侧偏角可表示为
(5)
式中:δf和δr分别为前后轮转向角. 同时考虑车辆的四轮转向与四轮驱动,则车辆系统方程可表示为
(6)
式中

1.2 路径跟踪模型
车辆路径跟踪控制的目的是通过实时的车辆动力学控制,使得当前车辆距期望路径的横向偏差与航向偏差尽可能小,从而可建立如图2所示的车辆路径跟踪模型. 航向偏差及其微分方程可表示为
(7)
式中:ψ为航向偏差;ψh为实际的车辆航向角;ψd为期望的车辆航向角.ψh和ψd可表示为
(8)
式中ρ为期望路径的曲率半径. 利用Serret-Frenet方程,路径跟踪横向偏差方程为
(9)

图2 车辆路径跟踪模型Fig.2 Vehicle path following model
考虑到航向偏差角度相对来说较小,则式(9)可简化为
(10)
将式(7)和式(10)及其微分方程代入到式(9),可得车辆路径跟踪模型为
(11)
式中
xb=[x1x2x3x4]T;

2 车辆路径跟踪控制器设计
2.1 整体控制思路
对于四轮驱动四轮转向的无人车辆,采用分层控制的方式进行车辆路径跟踪的整体实现. 在上层控制器中,控制目标为通过设计适当的控制率使路径跟踪过程中的横向偏差和航向偏差趋近于0,根据当前的横向偏差与航向偏差,得到所需的车辆系统控制输入,即前后轮转角以及车辆横摆力矩. 在下层控制器中,通过4个车轮轮胎力的实时优化分配,满足上层控制器指令的车辆横摆力矩的控制需求.
2.2 基于Hamilton理论的控制器设计
式(11)中的路径跟踪模型可表示为
(12)
式中:
车辆路径跟踪过程中,控制目标为式(12)中的状态量趋于0,因此有别于常见的状态反馈控制,此时在控制层面上控制器目标相当于式(12)系统的自我镇定控制. 为了提高车辆路径跟踪系统的可靠性,在Hamilton控制理论的框架下,基于能量函数设计车辆上层控制器.
选取Hamilton能量函数为
(13)
从而系统(12)可转化为如下的Hamilton系统
(14)
式中:y为系统输入;f为系统干扰;
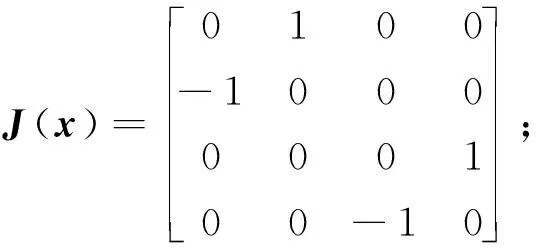
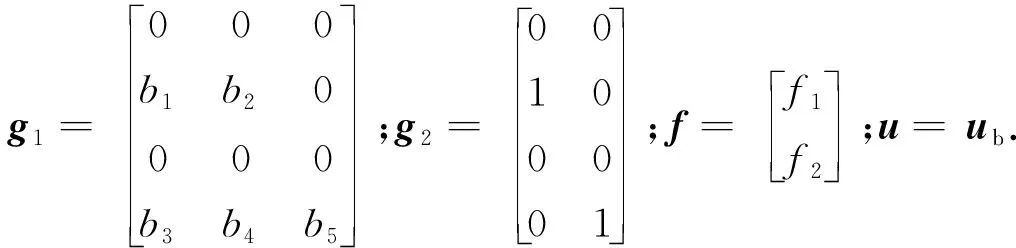
基于系统(14),控制器设计问题为:对于给定的抑制水平λ,设计反馈控制率u使闭环系统的L2增益不大于λ. 状态反馈控制率设计为
(15)
将式(15)代入式(14)可得
(16)
选取Lyapunov函数为V(x)=H(x)≥0,则系统Hamiltonian-Jacobian不等式为
(17)

2.3 轮胎力优化分配
四轮驱动四轮转向无人车的4个轮胎驱动力都可以独立控制与分配,这一优点为无人车辆的路径跟踪控制提供了更高的操纵自由度. 在下层控制器中,根据上层控制器得到的车辆横摆力矩,利用二次规划法动态分配4个车轮纵向力. 目标函数为
(BxFx-ΔMz)TW2(BxFx-ΔMz),
(18)
式中:

其中,B1=-cosδfbs+lfsinδf;B2=cosδfbs+lfsinδf;B3=cosδfbs+lfsinδf;B4=cosδfbs+lfsinδf.
W1和W2为权重矩阵. 权重矩阵W1用于调节轮胎纵向力的大小,目标函数中的J1用于保证车辆的驱动能力且避免轮胎纵向滑移. 权重矩阵W2用于调节J2的大小并满足上层控制器的横摆力矩需求.
对目标函数求偏导可得
(19)
(20)
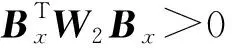
(21)
3 仿真验证
为验证所提出的无人车路径跟踪控制方法的效果,基于CarSim和Simulink搭建联合仿真平台并进行车辆路径跟踪仿真分析,其中CarSim用于提供整车动力学模型,所设计的控制器以及轮胎力分配方法在Simulink中实现. 车辆仿真参数如表1所示.

表1 车辆参数
仿真时,车速为20 m/s,道路附着系数为0.5,仿真工况设定为车辆换道:起步瞬间车辆行驶方向与道路方向平行,然后期望路径的曲率从0逐渐增大,当达到换道中心线时,期望路径的曲率突变为当前曲率的负数并逐渐趋于0.
车辆路径跟踪控制效果如图3所示. 图3(a)中,实际的车辆路径能较好地跟踪期望路径的变化趋势,计算可得路径跟踪精度达到了96.31%,从而验证文中方法具有较好的路径跟踪控制能力. 从图3(b)中可以看出,在上半段路程中,车辆实际路径的曲率能够跟踪期望路径曲率,跟踪精度和实时性都满足要求. 在下半段路程中,由于道路曲率的突变,路径曲率的跟踪误差稍大,但误差相对来说仍然是收敛的,且在可容许范围内.
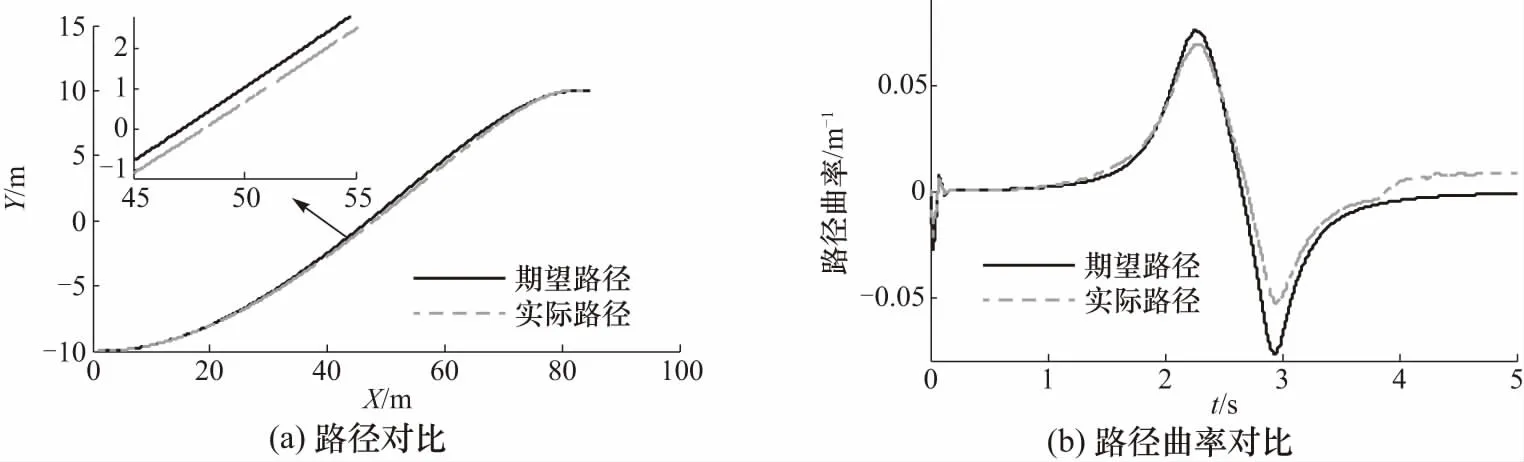
图3 路径跟踪效果Fig.3 Effects of path following control
车辆路径跟踪的横向误差和航向误差变化如图4所示,观察可知,横向误差从0开始增大到0.4 m后又逐渐减小,而航向误差的大小大约在-1.2°~1.5°之间波动. 计算可得横向误差和航向误差的平均值为0.150 7和0.209 7,标准差为0.155 6和0.327 4,说明换道过程中,路径跟踪的横向误差和航向误差都受控于一个较小的误差范围,从而证明所提出的控制方法能较好地保证车辆路径跟踪的控制精度.

图4 路径跟踪误差Fig.4 Error of path following
图5所示为上层控制器计算所得的车辆前后轮转角控制需求. 由图5(a)和图5(b)可知,前后轮转向角变化范围分别约为-4°~7°和-3°~5°之间. 通过图5(a)、图5(b)与图4(b)的对比可知,前后轮的车辆转角变化趋势与实际路径与期望路径之间的航向误差的变化趋势基本一致且在数值上的正负相反,说明路径跟踪控制器能够根据车辆的航向误差实时调节车辆转向,从而使车辆的实际路径动态地趋于期望路径. 图6所示为4个车轮纵向轮胎力分配控制结果. 图6(a)为上层控制器计算所得的横摆力矩控制需求,图6(b)为下层控制器根据横摆力矩所得的4个车轮的轮胎力. 观察可知,在车辆转向过程中,处于对角线位置的车轮纵向力总是交替地增加与减小,且增减的变化趋势与前后轮转角以及航向误差的变化趋势大体一致,说明了控制器具有较好的自适应调节能力. 此外,车辆前轴内轮和后轴外轮的纵向轮胎力总是大于另外两个车轮的纵向力,这种分配方式有助于减小车辆转向时的转向行驶阻力,提高车辆的不足转向趋势和横摆稳定性.
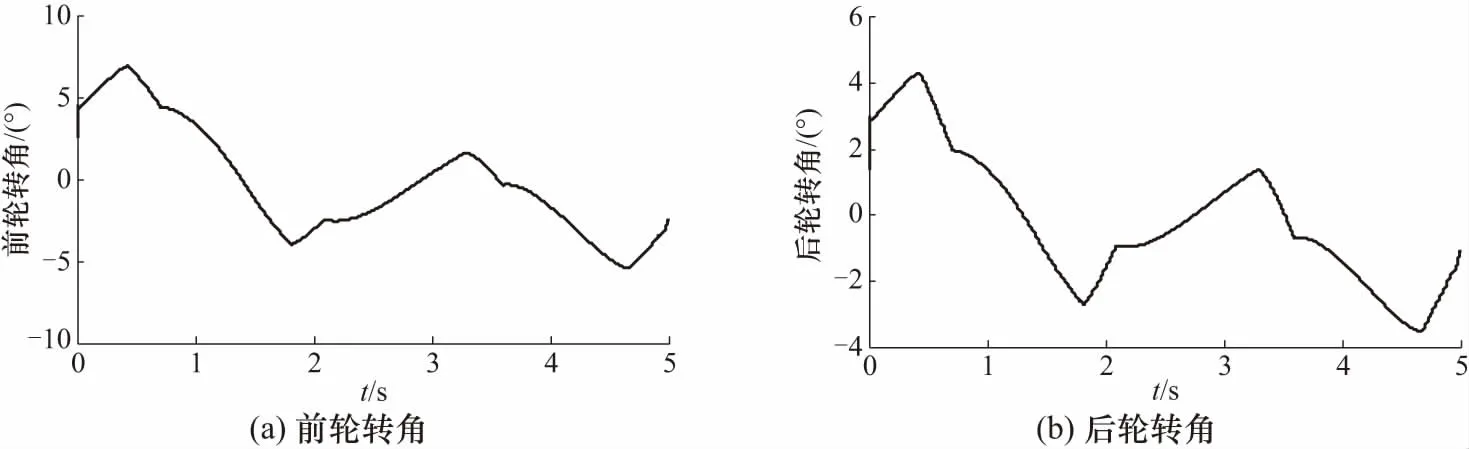
图5 前后轮转角的控制输入量Fig.5 Control efforts of front and rear wheel steering angle
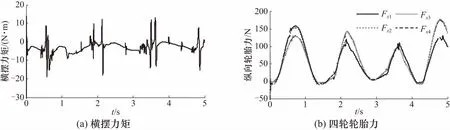
图6 轮胎力分配结果Fig.6 Results of tire force allocation
4 结 论
针对四轮驱动四轮转向无人车辆,利用车辆动力学方程和路径跟踪方程建立了车辆路径跟踪误差模型,设计了基于此误差模型车辆控制目标.
设计了路径跟踪分层控制结构,在上层控制器中,根据车辆路径跟踪误差模型,基于Hamilton理论设计上层控制算法,提高路径跟踪精度和系统的鲁棒性,同时在下层控制器中设计四轮轮胎力分配方法,用于执行上层控制器计算得到的车辆控制需求.
利用CarSim和Simulink联合仿真模型进行了仿真实验,结果表明所提出的控制方法能够将车辆路径跟踪过程中的横向误差和航向误差控制在较小的范围内并趋于收敛,说明路径跟踪的精度和可靠性都能得以保证.
文中研究了路径跟踪控制问题,但尚未考虑无人车辆行驶过程中车辆的稳定性控制问题. 同时,文中尚未考虑模型不确定性,非线性干扰以及系统时滞等因素对控制的影响. 今后将对以上问题进行深入研究.
