控制学科在环的主动悬架多学科设计优化

陈潇凯, 雷浩, 刘佳辉, 李孟强

(北京理工大学 机械与车辆学院，北京 100081)

主动悬架技术是改善车辆动力学性能的主要研究方向之一. 如对于越野车辆，其通常具有较大的刚度、阻尼和质心高度，在普通道路上行驶时的平顺性、高速操纵稳定性和平均行驶速度都不理想，而主动悬架可以使越野车辆兼顾越野行驶和道路行驶[1]. 近年来，主动悬架技术的研究取得了一定的进展，秦也辰等[2]提出了主动悬架的力跟踪控制方法，利用PI控制算法跟踪作动器输出的控制力. 么鸣涛等[3]应用微分几何理论对油气悬架非线性系统进行了线性化，并利用LQR控制器实现了半主动悬架的控制. 但从系统层级上，综合考虑主动悬架的结构参数和控制参数协同作用的研究较少. 本文利用多学科设计优化方法，对主动悬架的设计优化进行研究.

多学科设计优化方法是一种通过充分探索和利用系统中相互作用的协同机制来设计复杂系统和子系统的方法论. 汽车是一类典型的复杂系统，其设计涉及多门学科，且各学科之间相互作用，相互影响. 而在涉及到系统的控制问题时，传统的设计思路往往是把控制问题置于系统的结构设计和优化之外[4]，如图1所示(以主动悬架的设计为例). 这样并没有充分考虑到控制学科和系统结构设计之间相互影响的协同效应，很有可能导致最终设计失去系统的整体最优解. 本文利用多学科设计优化的思想，将控制学科纳入到系统的设计优化回路内，如图2所示，进行控制学科在环的多学科设计优化研究. 这样可以更好地处理学科之间的耦合关系，对系统结构参数和控制参数进行协调，以获取系统的整体最优解[5-10].

图1 传统设计流程Fig.1 Traditional design flowchart

图2 控制学科在环的多学科优化设计流程Fig.2 MDO flowchart with control disciplinary in loop

1 车辆模型和控制系统的建立

1.1 车辆模型的建立

本文以1/4车辆模型为例(忽略轮胎阻尼)，如图3所示.

图3 含主动悬架的二自由度1/4车辆模型Fig.3 2 DOF quarter-vehicle model with active suspension

主动悬架系统的运动方程为

(1)

式中：Ms为簧载质量；Mu为非簧载质量；kt为轮胎垂向刚度；ks为悬架线刚度；cs为阻尼系数；Fu为作动器作用力.

利用滤波白噪声法对来自路面的随机激励进行模拟，车轮受到的路面激励为

(2)

式中：f0为下截止频率；G0为路面不平度系数；v0为车速；z0为路面垂直位移输入；w为单位强度的高斯白噪声信号.

1.2 控制系统的建立

(3)

式中：

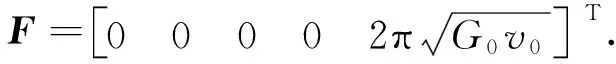
在评价车辆的动力学性能时，通常选取车身加速度、悬架动行程、轮胎动挠度作为评价指标，选输出向量为

故式(3)中：

本文中采用的主动悬架控制器为线性二次高斯最优控制(linear quadratic gaussian, LQG)控制器[5]. 假设所有状态变量均是可测量的. 选取状态变量和控制变量二次型函数的积分作为性能指标，即

(4)

式中Q,R,N均为权重矩阵.

本例中，对作动器作用力，车身加速度，悬架动行程，轮胎动挠度进行综合考虑，取

q3(z1-z2)2+q4(z0-z1)2]dt,

(5)

式中qi(i=1～4)为加权系数. 以车身加速度为基准，故取q2=1.

若将式(5)整理成式(4)的标准二次型，可得权重矩阵Q,R,N为

矩阵Q与悬架动行程和轮胎动挠度的加权系数q3,q4有关；R与作动器作用力的加权系数q1有关. 不同的加权系数对系统的特性具有不同的影响，因此，在设计时需要合理选取加权系数的值，当某个分量需要特别约束时，可增大该分量的加权系数[5].

当车辆参数和加权系数值确定后，最优控制反馈增益矩阵K可由黎卡提方程求出[6]

PA+ATP-(PB+N)R-1(BTP+NT)+Q=0,

(6)

K=R-1(BTP+NT).

(7)

根据任意时刻的反馈状态变量x(t)，可得到LQG控制的线性控制律：

Fu(t)=-Kx(t).

(8)

2 多学科设计优化问题描述

多学科设计优化问题，在数学形式上通常可简单表达为

① 寻找:xd;

② 最小化:f=f(xd,y);

③ 约束:

hi(xd,y)=0(i=1,2,…,m),

gj(xd,y)≤0(j=1,2,…,n).

式中：xd为设计变量；f为目标函数；y为中间变量；hi(xd,y)为等式约束；gj(xd,y)为不等式约束.

在本例中，设计变量包括悬架参数和控制参数，分别为悬架线刚度ks；阻尼系数cs；轮胎垂向刚度kt；以及LQG控制器的控制参数q1,q3,q4.

目标函数除了要考虑车辆的动力学性能指标外，还需要考虑作动器在控制过程中所消耗的能量，消耗能量过大会导致车辆的能耗增加，影响车辆的经济性. 因此，目标函数可定义为作动器作用力、车身加速度、悬架动行程、轮胎动挠度均方根值的加权和，即

(9)

式中ρ1，ρ3，ρ4为权重系数.

同时，将簧载质量部分的偏频在一定的范围内作为优化问题的约束条件，即

(10)

式中kr=ktks/(kt+ks).

本文基于多学科可行法(MDF)的思想，搭建主动悬架设计优化框架，如图4所示. 其中，系统层优化器根据优化算法，调整系统的设计变量值，进行多学科分析，多学科分析根据车辆模型和LQG控制模型得到性能指标，反馈给系统层，系统层再根据反馈结果调整设计变量，重新进行多学科分析，直到迭代过程收敛，获得最优解.

图4 主动悬架MDF优化方法示意图Fig.4 Schematic representation of MDF method for active suspension

3 优化结果分析

本例的参数取值和设计变量的取值范围如表1所示.

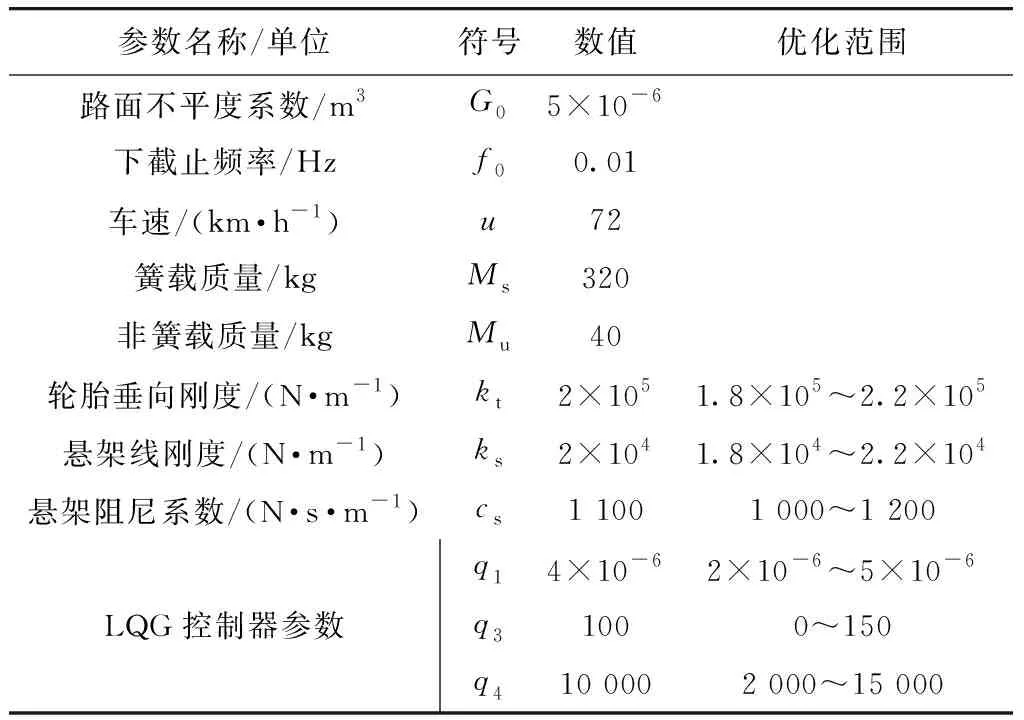
表1 参数取值及设计变量的取值范围

基于MDF优化框架，采用模式搜索(Hooke-Jeeves, HJ)算法对主动悬架进行优化，优化过程中目标函数的收敛过程如图5所示. 由图5可以看出，在MDF的优化框架下，目标函数值逐渐向最优解进行逼近，并最终收敛.

图5 目标函数收敛过程Fig.5 Convergence process of the objective function

优化后的主动悬架与原始主动悬架相比，各项性能指标的均方根值如表2所示. 其中，优化前后的车身加速度-时间响应如图6所示.

表2 优化前后的性能指标均方根值

Tab.2 RMS of performance index before and after optimization

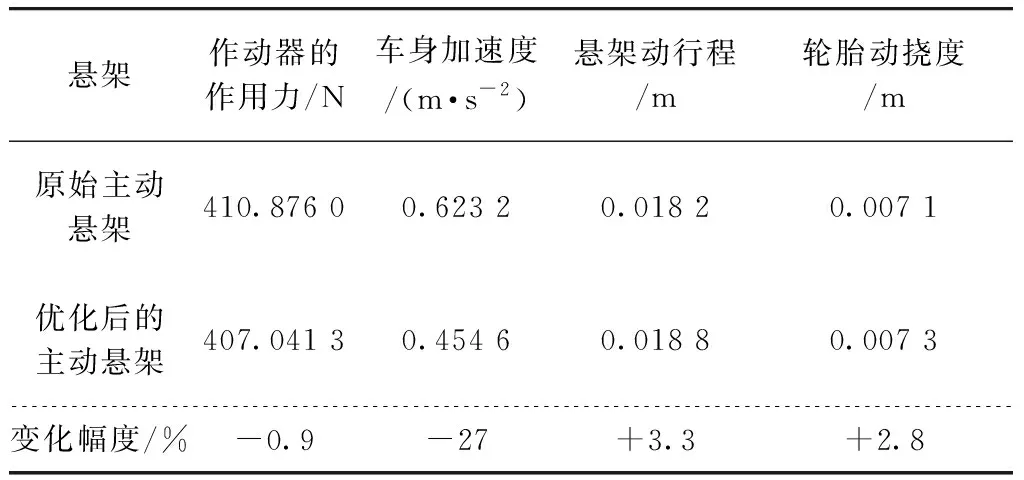
悬架作动器的作用力/N车身加速度/(m·s-2)悬架动行程/m轮胎动挠度/m原始主动悬架410.876 00.623 20.018 20.007 1优化后的主动悬架407.041 30.454 60.018 80.007 3变化幅度/%-0.9-27+3.3+2.8

可以看出，经过优化后，车身加速度的均方根值明显减小，减小幅度达27%；同时，作动器的作用力略微减小，悬架动行程和轮胎动挠度略微增大. 对比优化前后的结果说明：经过考虑控制的多学科设计优化后的主动悬架，在能够保证悬架的工作空间和轮胎变形在一定的范围内，且不消耗更多的能量的前提下，对乘坐舒适性有了显著改善.

4 结 论

基于MDO的思想，将控制学科纳入设计优化的框架内，进行控制学科在环的多学科设计优化研究. 并以主动悬架的优化设计为例，建立了采用LQG控制器的主动悬架1/4车辆模型，采用多学科可行法(MDF)搭建了主动悬架的优化框架，对悬架的结构参数和控制参数同时进行优化. 对比优化前后的性能指标，该方法能显著改善车辆的舒适性，并能协调好悬架参数和控制参数之间的关系，获取整体最优解. 优化后的主动悬架在能够保证悬架的工作空间和轮胎变形在一定的范围内，且不消耗更多能量的前提下，改善了车辆的乘坐舒适性.