基于神经网络模型的室内大规模人流密度预测

宋宇波， 彭朝阳， 苏悦， 刘蕴箫， 赵千锋， 朱珍超

(东南大学 网络空间安全学院,江苏省计算机网络技术重点实验室，江苏，南京 211189)

随着城市化进程的日益加快，城市人口急剧攀升，一些大型的室内场所出现了人群拥挤的难题. 如大型商场、火车站、医院等场所，这些场所人群密度和客流量很大，给人们活动造成不便，存在安全隐患，甚至可能发生踩踏事件[1]. 如果能够预知某个区域内的人流密度，就能够根据具体需要提前做好防范措施，如安排工作人员进行引导，开辟疏导人群的通道等. 人们可根据自身需求选择较为通畅的路径，便能很好地解决人群拥挤的问题.

人流密度监控和预测是解决上述问题的关键步骤之一. 通常两种方法用来对人流密度进行人监测——基于视频监控以及基于射频信号.

一种常规的方案是基于视频监控记录人的身体或者头部图像. 这种方案首先建立头和身体的模型，然后去和视频监控中的画面进行图像匹配，从而收集到一些有用的信息，如协方差矩阵、梯度直方图(HOG)等[2-3]. 如Stan Birchfield[4]利用人头部的二维模型作为匹配特征进行了相关工作. 但是人影重叠，这种方案不适用于人流密度特别大的场合. 因此Marana等[5]使用纹理去描述不同的人群密度，他们发现人流密度小的时候纹理粗糙，而人流密度大的时候纹理精细，因此可以通过纹理的精细程度来描述人流密度的大小. 这类方案一般是基于面积、纹理、边缘等特征的统计. 此外还有Ryan等[6]使用的面积法、边缘法等. 但是这些方法都需要所监控人群的动态信息. 然而，对于商场餐饮区等特定的场所，人们用餐时基本是静态的. 因此以上方法不适用于人们动作较少的场所. 除此之外，基于视频监控的方案都牵涉到个人隐私问题，在许多敏感的场合并不适用[7].

除了视频监控的方案之外，基于射频信号的方案[8]也引起了广泛的研究. 此种方案通常是先采集手机的无线信号，然后对采集到的信号进行加工和分析——先对人进行定位[9]，再由定位信息来统计密度. 但是传统基于射频信号的方案只是将所采集信号按照信号源进行归类，将归类后的类别数作为估算数目. 此种方案忽视了由于信号源与捕获点间距离远近的差异而产生不同贡献度的因素，从而导致了人流密度估算结果具有偏差.

对于人流密度预测这一问题，目前一种主流的预测方案是基于回归分析实现的[10]. 回归分析法由于在分析多因素模型时简单下方便，所以有着广泛的应用. 它首先确定自变量和因变量，然后根据历史数据建立数学回归方程模型. 模型要求预测误差尽可能的小，一般遵循最小均方误差准则(MMSE). 然而通过回归分析法所得到的数学方程需要大量的计算，方能得到一个静态的数学模型. 对于不确定性大，要求能够及时适应场景的的场所并不适用. 本文所适用的场景是医院、大型商场等大规模室内场所，客流量变化明显，不确定因素较多，因此回归分析法并不合适.

针对基于视频监控和射频信号等方案存在的问题以及回归分析法的局限性，本文在采集手机WiFi信号的基础之上，根据信号的强度对其进行加权运算，并提出了一种基于神经网络的新型方案. 因为当今社会智能手机基本人手一部，而某个区域的人流密度是一个大致的人数范围，并不需要特别精确的数值，所以个别没有携带手机的人只会对估计结果产生轻微的影响，所以可以通过某个区域内手机的数量来侧面估计人的数量. 因此，对人流的统计就转变为对手机数量的统计. 为了消除统计手机数量时由于距离因素产生的估算偏差本文提出了新型的室内人流密度估算算法，该算法以现有的基于射频信号进行密度估算算法为基础，引入加权运算来提升估算质量. 并且该算法直接对手机信号强度数据集进行处理，得到一个预测模型，省去了传统方案先得到人数再进行预测的步骤，很大程度上节省了工作量. 另一方面，由于WiFi信号具有穿透性，避免了视频监控方案所存在的遮挡问题. 本文采用了手机WiFi信号处理和神经网络预测的方法，建立了一种新型的大规模室内人流密度预测模型框架.

1 整体结构

1.1 整体框架

本文采用了手机设备信息处理和神经网络预测的方法，建立了一种新型的统一的人流密度预测模型框架，该框架包括两个阶段：训练阶段和验证阶段，如图1所示. 在训练阶段中将手机发出的WiFi信号作为数据来源，WiFi信号中包含mac地址和信号强度等信息. 把WiFi信号按mac地址去重之后，基于信号强度进行加权运算，得到监测范围内的手机数量估算值. 将每个时间段内的手机数量估算值都存入数据库当中，同时作为特征输入送入BP神经网络进行模型训练，得到预测模型. 在验证阶段，用户上传位置信息，与数据库中的预测位置进行匹配，获取所预测位置连续若干个时间段内的手机数量，然后将手机数量送入预测模型，得到人流密度预测值. 预测值与裁决器中预设阈值进行比较，得到预测位置的人流密度等级.

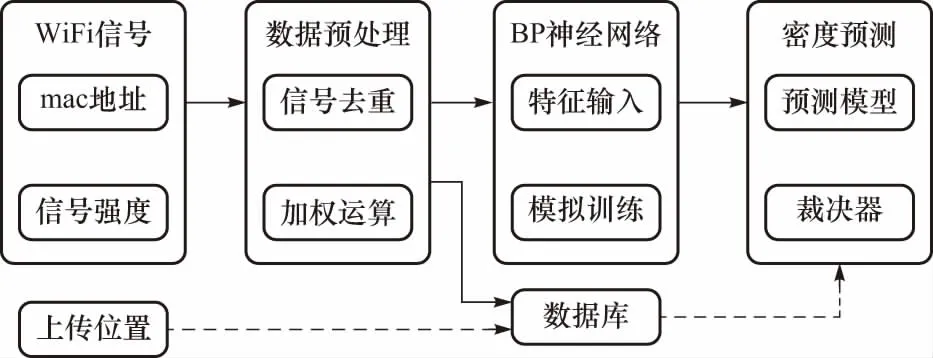
图1 密度预测流程Fig.1 The density prediction process

1.2 训练阶段

① WiFi信号：由于智能手机十分普及，并且手机的信号容易获取，所以本文以手机WiFi信号作为数据来源的载体. 在WiFi开关打开的状态下，手机会发出WiFi信号. 这些信号在空气中传播并随着传播距离增加而衰减，其中携带了信号的强度信息和每部手机唯一对应的mac地址[11].

② 数据预处理：因为对下一个时刻的人数进行预测需要此前若干个连续时间段内的统计人数，所以要对数据采集部分所得到的手机信号进行数据预处理. 因为每部手机的mac是独一无二的，所以可以用于与其他手机进行区分. 将获取到的信号按照mac地址进行去重便粗略得到了手机数量. 但随着手机与捕获点的距离增大，对捕获区域的贡献度减小，因此简单地统计手机数目会造成统计结果偏大. 为了解决统计结果偏大的问题，本文提出了一种基于信道衰减模型的加权算法. 该算法利用信号强度与距离的关系，将信号强度处理之后获得加权系数，最终加权求和所得结果即为捕获区域内有效的统计人数. 把统计人数上传至数据库以便验证使用.

③ BP神经网络：在模型训练阶段，本文采用BP神经网络[12-13]. 本文将在某特定区域中若干个连续时间周期内加权统计后的人数作为输入层，经过隐含层的加权和非线性变换，对下一个时间周期内该区域内的人数进行预测，将预测结果作为BP神经网络的输出层. 训练结束之后便可得到预测模型.

1.3 验证阶段

在验证阶段中，用户根据需求上传所要预测区域的位置信息，与数据库进行匹配，调用该区域过去时间段内所得的统计人数. 将统计人数作为特征输入送入训练好的预测模型得到预测值. 裁决器将预测值根据预设阈值划分人流密度等级.

2 基于信号强度加权的人流密度估算算法

手机与捕获点的距离不同，其对捕获区域的贡献度也不同. 距离越远，那么该手机对人流密度的贡献度也就越小. 由于距离关系在现实环境中不易测量，所以本文将距离信息转换为信号的强度信息. 根据RSSI测距原理[14]，WiFi信号在空气中传播时，遵循信号衰减模型. 随着手机与捕获点之间距离的增加，信号强度会逐渐减弱信号强度和传播距离由接收功率和发射功率表征，具体关系如下

10lgPR=10lgPT-10nlgr.

(1)

式中:PR为接收功率(dBm);PT为发射功率(dBm);r为收发单元间的距离;n为传播因子，其数值取决于传播环境.

由式(1)可以看出捕获设备所抓取信号的强度随着手机距捕获设备的距离增大而减小.

因为手机与捕获点的距离是连续变化的，而加权的系数是按照阈值设定离散化的，所以要将距离离散化. 以捕获点为圆心，手机和捕获点间距离记为r，设定单位值R，那么离散化之后的距离a可表示为

(2)

以捕获点为圆心，离散化后圆的面积与(aR)2成正比. 将以单位值R为半径差的一系列圆环面积记为S，则S的比例关系由式(3)给出为

S1∶S2∶…∶Sa=1∶3∶…∶(2a-1).

(3)

假设所有地方人流均匀分布，则每个环形区域对应的面积比即为人数比，又因为假设人流均匀分布，故权重系数与面积的乘积可认为是一个定值，不妨记为1，因此给出权重系数c的表达式为

c=1/(2a-1).

(4)

将式(4)作为权重对式(2)进行加权，则捕获设备统计到的手机数量为

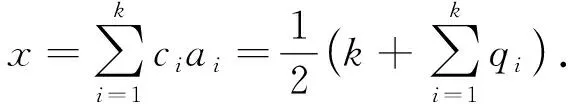
(5)

其中k为根据mac地址去重之后未加权的手机数目，qi由式(6)给出

(6)

将式(1)写成指数形式，用接收信号和发射信号强度来表征收发点间距离r

(7)

将收发点间距离r代入式(6)，所得的qi作为被加权变量整体代入式(5)，并假设发射功率为常数A，于是得到了一个基于信号强度加权的估算算法

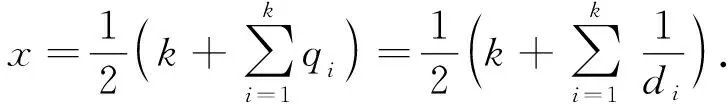
(8)

式中:x为经加权运算之后捕获设备统计到的手机数量；k为加权之前的手机数目，为方便表示，用di表示加权变量，di由式(9)给出

(9)

3 基于神经网络的预测模型

在模型训练阶段，本文采用BP神经网络. 本文将在某特定区域中若干个连续时间周期内加权统计后的人数作为输入层，经过隐含层的加权和非线性变换，对下一个时间周期内该区域内的人数进行预测，将预测结果作为BP神经网络的输出层.

利用上文提出的基于信号强度加权估算的算法，可得到一个时间段内某特定区域内的人流密度估算值. 连续估算N个时间段的人流密度，并按序排列，记为矩阵X

X=[x1x2…xN].

(10)

隐含层的作用是将输入的特征经过加权计算而并非线性变化，它由若干个加权矩阵W和偏置矩阵B组成. 矩阵W和B的各个元素随着神经网络训练过程自动调整. 因此，将连续N个时间段的估算人数X作为BP神经网络的输入，通过隐含层进行参数自动调整，对接下来一个时间段的人数做预测，公式由式(11)给出为

(当j=m时，outm=predict).

(11)

预测输出和实际输出存在差别，将此误差平方作为损失函数，若想得到一个准确的预测模型，则要最小化损失函数. 由于Adam(adaptive moment estimation)的每一次迭代学习率都有一个固定范围，所得到的参数比较平稳，同时其速度要快于梯度下降法. 为了能够快速建立预测模型，适应波动性较大的场所，本文采用Adam算法[15]. 在最小化损失函数的过程中，矩阵W和矩阵B会自动调节参数. 训练之后便得到了一个训练好的预测模型.

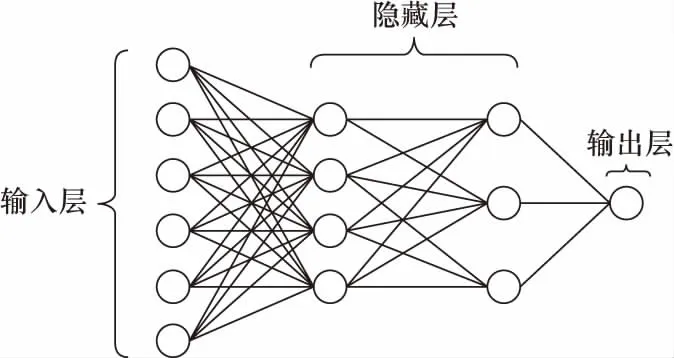
图2 多层预测网络Fig.2 Multi-layer prediction network

4 实验结果分析

本文将某购物中心餐饮区作为测试地点. 每间隔10 min刷新一次捕获到的移动设备信号强度及对应的信息. 经过多次实际信号采集，分析出信号数据的变化趋势. 信号强度加权获得客流量后，将客流量作为输入，构建训练集和测试集. 训练集的数据经过多次迭代后获得一个预测模型，最终使用测试集进行测试.

4.1 测试过程

由于当今社会基本达到人手一部智能手机，室内的手机数量可以反映出该区域的人流量. 本文在某购物中心餐饮区进行了以下测试. 该购物中心地图如图3所示.

图3 购物中心地图Fig.3 Map of global shopping center

在餐饮区设置一个捕获设备. 本文中使用树莓派作为捕获设备. 将树莓派与设置为监听模式的无线网卡组合，可以用来捕获其周围手机的设备信息，这些信息包括mac地址、捕获的时间以及信号强度等. mac地址用于区分不同的手机，每捕获到一个新的mac地址即意味着附近有一个新的手机用户，对应地客流量增加. 捕获时间显示捕获设备抓取到手机数据包的时刻；信号强度则侧面反映出所捕获到的信号源距离捕获设备的距离，信号强度越大，就说明信号源距离捕获点越近，对人数的统计越有意义. 设定不同的阈值，并将信号强度与之比较进而对信号的有效统计程度赋予不同的权重，有助于更准确地计算一个特定区域的人流密度. 将设备的信息按照mac地址的不同进行去重后便得到了某个时刻捕获点周围的人数.

通过构建好的训练集进行训练模型训练. 从图4中可以看出前20次的迭代过程中损失函数急剧下降，并且随着迭代次数的继续增加，损失函数趋于平缓，迭代50次之后基本不变，此时可认为迭代结束，得到训练模型.

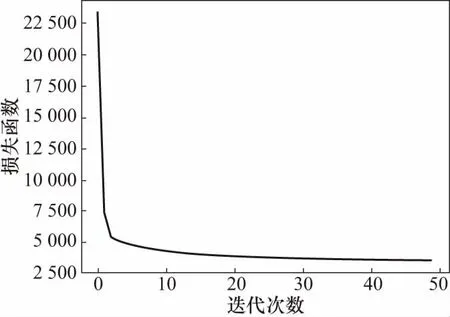
图4 损失函数下降曲线Fig.4 The decline curve of loss function

4.2 测试结果

在商场餐饮区每天10∶00—21∶00区间进行测试，将测试集送入上述已经训练好的模型中进行测试，并把预测值与通过分析数据包所得到的真实数值进行对比. 折线图5绘制了统计的真实人数和预测输出人数在每个时间段内的折线图. 捕获设备每间隔10 min刷新一次数据，选取每个小时中的第20～40 min区间内的平均人数作为该小时的有效统计人数. 柱状图6给出了各个时间段内预测输出的精度. 表1给出了具体的人数信息、精确度的数值和平均预测准确率，其中平均预测准确率由一天内各个时间段的准确率求算数平均给出.

图5 预测人数和真实人数对比Fig.5 Comparison of predicted and actual numbers

图6 各个时间段的预测准确率Fig.6 Prediction accuracy of each time period

由图5可以看出，真实平均人数和预测平均人数走势变化基本一致. 在11∶00—13∶00这段用餐高峰期出现峰值，随后人流密度迅速下降，直到16∶00时候又开始呈现上升趋势，进入晚餐用餐期，并在18∶00—19∶00时间段内达到晚餐高峰期，随后人流密度再次呈现下降趋势.

由图6可以看出，在15∶00—16∶00以及20∶00—21∶00两个时间段内，预测准确率相对其他时间段偏低. 这是因为在用餐高峰期过后，用餐人数急剧减少，人们活动的不确定性增大，所以此时预测准确率下降.

由表1中可以看出，除20∶00—21∶00外，其余每个时间段的预测准确率都在90%以上. 经计算总体的准确率为94.70%. 由于在20∶00—21∶00时间段内用餐的人很少，并且处于商场即将停止营业之前，所以这个时间段内的人流变化随机性较大，导致预测准确率较低，仅有84.74%.

表1 真实人数、预测人数和准确率Tab.1 True number, forecasted number and accuracy

5 结束语

基于对手机WiFi信号的处理，提出了一种适应于大规模室内场所的人流密度预测方案. 该方案将手机WiFi信号进行加权处理，其结果送入神经网络进行预测. 在人流密度估计问题上，本文所提方案一方面解决了视频监控方案的遮挡问题，另一方面避免了传统基于射频信号方案不准确性. 在预测模型构建问题上，相比于线性回归法，神经网络预测法更适合于商场、火车站等人流随机性大的场合. 实验结果表明，所得到的预测模型准确率达到了94.70%. 后续的研究中，将尝试采用多个捕获点同时预测，并通过加权投票的方式，进一步提高预测的准确率和可靠性.