用两种方法研究二维光子晶体的带隙结构

刘继平，张晓茹，刘 晗，杨涪铨，潘 庆，吴向尧

（吉林师范大学物理学院，吉林四平136000）

1987年Yablonovitch和John两人分别独立提出光子晶体的概念[1-2]。目前为止，国内外学者对于光子晶体的研究也取得了较为丰硕的成果[3-5]，例如Zhang等制备出一种多通道可调太赫兹滤波器[6]，Dai等设计出一种基于等离子体量子阱结构的双通道窄带可调滤波器[7]，Wu等提出光子晶体三极管等[8]。光子晶体是由介电常数不同的两种或两种以上材料构成的人工微结构，从维度角度可将光子晶体分为一维、二维和三维光子晶体。二维光子晶体的相关研究是目前国内外的研究热点。光子晶体中介质介电常数的形式有常规和函数之分，故又可将其分为常规光子晶体和函数光子晶体。光子晶体的主要特征有光子带隙、缺陷态、光局域化等[9-11]。当光在光子晶体中传播时，某些频率范围内的光会受到限制，形成光子禁带，在禁带中光的传播是被禁止的。当光子晶体的周期性结构被破坏时，如去掉一个或几个介质柱，改变其中一个或几个介质柱的折射率，这样在原来的带隙中就会出现一条或几条缺陷模式曲线，允许某些特定频率的光通过带隙，因此起到控制光子运动的作用。利用这一特性可以设计优化很多高性能设备，如发光二极管、半导体激光器、光学滤波器等[12-13]。光子晶体在TE和TM偏振下，均存在带隙结构，在TE和TM波带隙重合的区域，称为绝对带隙或完全带隙。一般情况下，光子晶体的禁带越宽，其性能就越稳定[14-15]。研究光子晶体常用的方法有平面波展开法、有限元法、传输矩阵法和时域有限差分法等[16-18]。

在文献[16]中，肖利等首次提出二维函数光子晶体的概念，所谓二维函数光子晶体，即组成光子晶体的介质柱的介电常数是空间坐标的函数，可通过外加电场光场实现将光子晶体介质柱的介电常数呈空间坐标形式分布，即通过电光效应和光学Kerr效应使介质柱介电常数成为空间坐标的分布函数。在本文中，基于二维常规和函数光子晶体在TE偏振下，用平面波展开法和COMSOL Multiphysics软件基于有限元法研究二者的带隙结构，比较两种方法的研究特点。通过对比研究我们得到一些经验结论，这为进一步研究二维函数光子晶体理论和利用函数光子晶体设计光学器件奠定了重要基础，并且提供重要的研究方法与思路。

1 二维光子晶体研究方法

1.1 平面波展开法

文献[16]中，用平面波展开法给出了TM和TE波的特征方程：

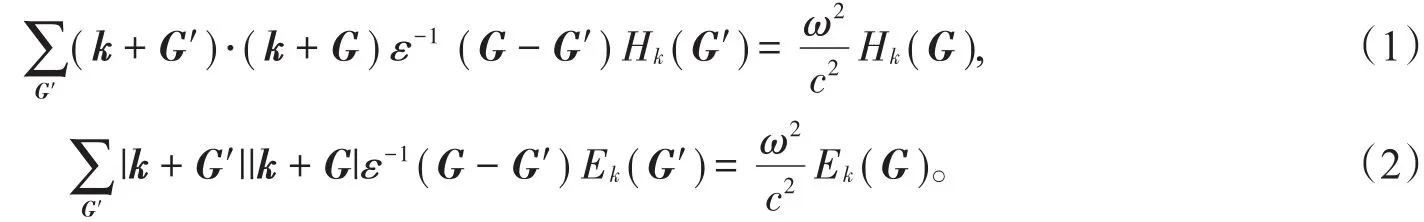
二维函数光子晶体介质柱的介电常数可以写为

即

由傅里叶逆变换得到

当εa(r)= εa，εa是常数，方程（5）可以变为

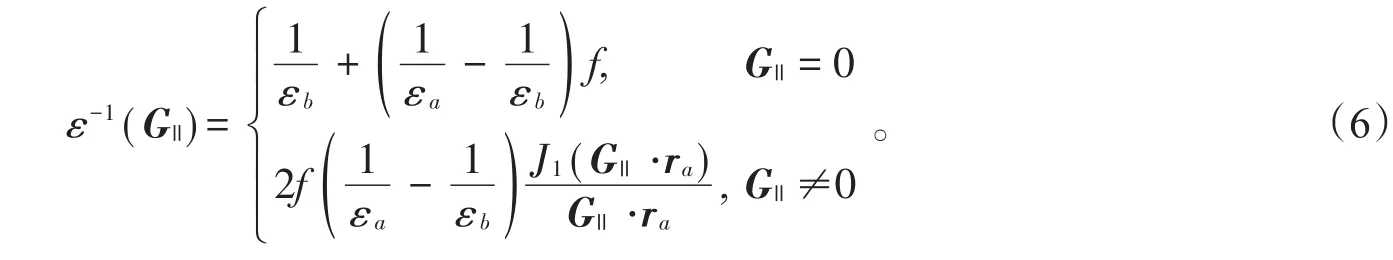
方程（6）是二维常规光子晶体介电常数的傅里叶变换。可见，二维常规光子晶体是二维函数光子晶体的一个特例。把方程（5）和（6）分别代入方程（1）和方程（2）中，可以得到二维函数光子晶体和二维常规光子晶体在TM和TE偏振下的带隙结构。

1.2 有限元法

有限元法（Finite Element Method,FED）[17]的主要思想是将连续场求解区域剖分成有限个离散的子域单元区域，并在每个离散的子单元中利用简单的函数来近似场值，然后将所有子单元的场值合成，逼近整个场域的解。

在本文中，基于COMSOL Multiphysics软件，利用Bom-Von Kannan周期性边界条件和Bloch波理论，将周期结构的有限元离散特征方程化归到一个周期单胞内的复系数特征方程，然后将其分为实部和虚部两组方程，并在周期单胞边界上应用Bloch定理，求解得到实数特征方程，获得频散曲线。具体来说，在COMSOL中，利用几何工具建立晶体模型最简单的单细胞结构，根据布洛赫定理，在单元格的4个边界上增加了两组周期性边界条件，并建立合适的网格，通过给定波矢k的范围，求解频率ω，得到色散曲线关系ω (k)，利用matlab软件编程转换数据，通过Origin画图得到二维光子晶体的色散关系曲线。

2 物理模型与数值分析

以二维正方结构光子晶体为例，由于光子晶体是周期性结构，所以选取光子晶体中的一个单胞进行计算。在二维光子晶体中，介质柱半径为ra=0.3a（晶格常数a=10-7m），背景介质为空气εb=1。对于二维常规光子晶体取介质柱的折射率n=3.42；对于二维函数光子晶体，取介质柱的介电常数为εr=k⋅r+b，其中k为函数系数，单位为1 m，b为无量纲参数。

图1（a）为正方结构二维光子晶体中的一个单胞，其中a1、a2为单胞的晶格矢量。图1（b）中，蓝色阴影部分是由3个高对称点Γ、Χ和Μ定义的简约布里渊区，三点坐标分别为为布洛赫波矢k的x，y分量。

图1 （a）定义正方单胞的晶格矢量a1和a2；（b）第一布里渊区扩展图

图2 为常规光子晶体的带隙结构图，其中介质柱的折射率n=3.42。图2（a）为通过平面波展开法计算得到的带隙结构，其中，第一条禁带的频率范围：0.238 6～0.318 9，第二条禁带：0.428 4～0.528 3，第三条禁带：0.670 5～0.701 0。图2（b）为通过COMSOL建模计算得到的带隙结构，其中，第一条禁带的频率范围：0.233 4～0.303 8，第二条禁带：0.412 7～0.516 9，第三条禁带：0.642 3～0.694 1。从2（a）与2（b）以及禁带频率范围的对比可以看出，两种计算方法得到的带隙结构图的能带分布基本相同，第一、二条禁带的位置及范围相差很小，第三条禁带的频率频率范围差距相对明显。

图3为函数光子晶体平面波展开法和COMSOL建模计算得到的带隙结构图，其中介质柱的函数介电常数ε(r)=5.6× 107⋅r+11.6964。在图2（a）中，第一条禁带频率范围：0.230 1～0.309 1，第二条禁带：0.410 7～0.520 2，第三条禁带：0.651 4～0.690 6。在图2（b）中，第一条禁带频率范围：0.224 1～0.291 7，第二条禁带：0.393 8～0.502 7，第三条禁带：0.620 8～0.680 6。从图2（a）与图2（b）以及禁带频率范围的对比可以看出，两种计算方法得到的带隙结构图的能带分布基本相同，第一、二条禁带的位置及范围相差很小，第三条禁带的频率频率范围差距相对明显。

图2和图3中，均是第三条禁带及以上通带的差别较大，这是频率所致。低频时，误差相对较小；高频时，其误差相对较大。关于频率造成误差的原因在文献[19]中有进一步的解释。平面波展开法与有限元法实质上都是求解电场的偏微分方程，只是运用的方法不同，两种算法计算同一参数下光子晶体带隙结构出现微小差距，原因在于两者的计算方法不同，得到的结果会有相应的误差，用COMSOL建模计算时，给定的波矢范围是个猜测值，取值会对计算结果又一定的影响，但是经过验证，一般取频率为光子晶体归一化频率的0.1～0.5倍，都能得到较好的计算结果。

图2 常规光子晶体在两种计算方法下的带隙结构图。

图3 函数光子在两种计算方法下的晶体的带隙结构图

3 结论

利用平面波展开法研究光子晶体带隙结构时，理论推导较为清晰，能够更加直观地理解光子晶体色散关系的求解过程，但是对于处理较复杂的光子晶体结构或含有缺陷的光子晶体结构时，该方法很难精确计算，甚至不能求解。利用基于有限元法COMSOL软件计算光子晶体能带时，虽然计算过程不能直观显示，但是COMSOL中能够结合超胞技术计算超胞的能带，该方法也可计算含缺陷的光子晶体能带，并能直观地看出光子在缺陷处的分布状态。与已有计算方法相比，该方法在适用性、难易程度、计算速度、精确度、收敛性等方面具有明显的优越性。