数学物理中一维泊松方程基本解的两种求法

周文杰，潘 婷，章礼华，马业万

（安庆师范大学物理与电气工程学院,安徽安庆246133）

泊松方程是一个在理论物理和机械工程等领域应用广泛的二阶椭圆型偏微分方程，含该方程的定解问题通常均可采用格林函数法进行求解。在物理上，求解泊松方程的边值问题本质上可以归结为求相对应的格林函数，然后通过将求得的格林函数代入相应的泊松方程解的积分公式，就可以得到该定解问题的解。利用格林函数法求解时，需要用到与之相对应的基本解。数学物理上通常将不同维度下无界空间的格林函数称为该维度上泊松方程的基本解。在国内外众多数学物理方法教材和参考文献中，如姚端正教授和德国顾樵教授在他们各自编写的数学物理方法教材中均着重讨论了三维和二维无界空间格林函数，并给出了十分详细的求解方法及解的结果[1-2]，张宏浩教授针对三维无界空间格林函数也给出了详细的傅里叶积分法求解过程[3]，但针对一维无界空间格林函数都鲜有讨论，显式的表达式也较为少见。为此，本文将在分析讨论三维和二维泊松方程基本解的基础上，分别采用类推法和积分解法，给出一维无界空间格林函数的表达式。

1 类推法求一维泊松方程的基本解

1.1 三维泊松方程的基本解

三维泊松方程的基本解，即三维无界空间格林函数G( )M,M0是下述含有三维δ函数的非齐次方程

为了求解三维无界空间上泊松方程（1），考虑到空间对称性，通过选取球坐标系（选择源点M0为坐标原点），利用傅里叶变换法[2]，可求得上述无界空间泊松方程（1）的基本解为

其中r为场点M到源点M0的距离，即r= ||MM0。

1.2 二维泊松方程的基本解

二维泊松方程的基本解，即二维无界平面所对应的格林函数满足下述含有二维δ函数的非齐次方程

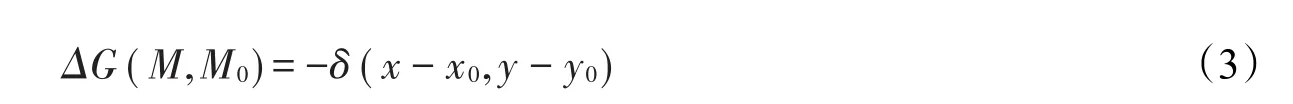
的解，其中二维δ函数可以表示为δ(M-M0)= δ(x-x0,y-y0)，M=M(x,y)，M0=M(x0,y0)，-∞ ＜ x,y ＜ +∞。

选取源点M0为坐标原点，在极坐标系下对（3）式求解[1]，可得二维无界平面上的格林函数为

其中r为二维平面上场点M到源点M0的距离，也即二维泊松方程的基本解为，它与垂直于XOY平面的具有单位线密度的无限长线电荷在r处所形成的电势函数相对应，其中ε为介电常数，这也正是二维泊松方程基本解的电势物理意义。

1.3 类推法求一维泊松方程的基本解

基于上述结果，下面从格林函数为势函数的物理意义出发，通过类推给出一维泊松方程的基本解。无界空间格林函数在三维情形下表示放置于坐标原点的单位点电荷在三维空间任意r= ||MM0=处所形成的电势，在二维情形下表示线密度ρ=1的垂直于XOY平面的无限长线电荷在处所形成的电势。单位点电荷可以看作是线密度ρ=1的无限长线电荷在原点处的投影，而线密度ρ=1的无限长线电荷可以视为面密度σ=1的无限大面电荷的投影。结合电磁学的知识[4]，面密度σ=1的垂直于x轴的无限大面电荷在一维空间任意r处产生的电势函数为φ=-r/2ε，其中ε为介电常数再结合三维和二维泊松方程基本解的表达形式和物理意义，可以类推给出一维泊松方程

的基本解，即一维无界空间格林函数，可以用面密度σ=1的垂直于x轴的无限大面电荷在一维空间任意r处形成的电势函数来表示，也即（5）式的基本解可以表示为

其中r表示x轴上点到平面的距离。将上述分析讨论的结果总结如表1所示。

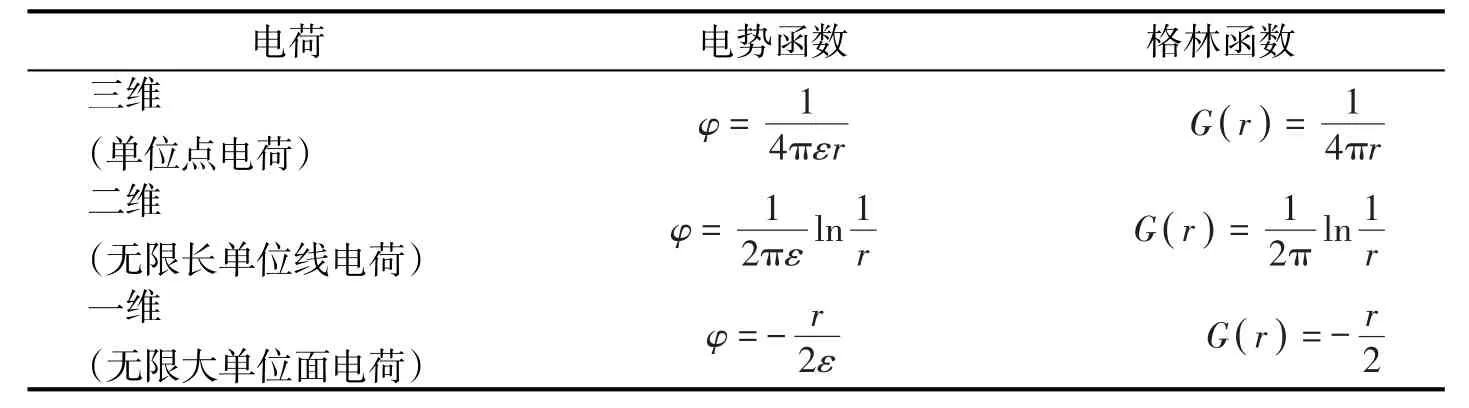
表1 三维、二维和一维情形下电势函数和格林函数

2 积分法求一维泊松方程的基本解

一维泊松方程的基本解即一维格林函数满足的泊松方程为

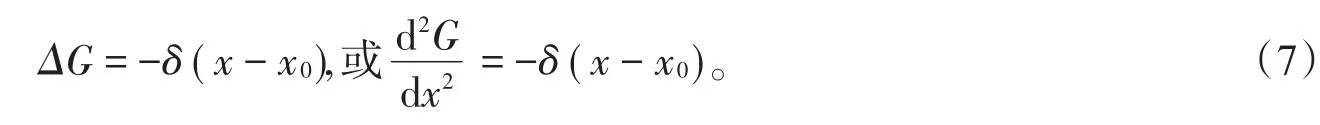
由δ函数的性质[5-6]可得

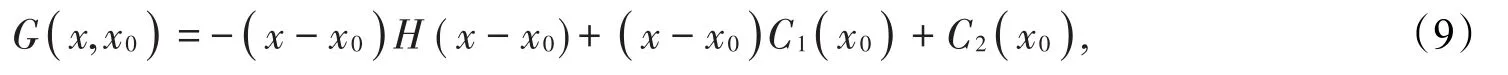
其中x0在物理上表示源点，考虑到G在物理上表示势函数，取x0处为零电势参考点，则C2( )x0=0。又由对称性可得根据阶跃函数的性质，有解得C1( )x0=则可得到格林函数为即

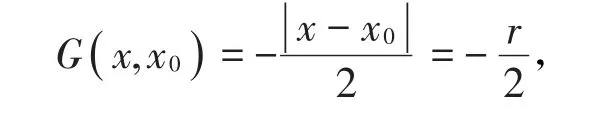
其中，r为x轴上的点到过源点x0且垂直于x轴的平面的距离。

3 结束语

综上所述，本文分析了三维和二维泊松方程基本解的电势物理意义，并运用类推的方法得出了一维泊松方程基本解，即一维无界空间格林函数的显式数学表达式。在此基础上，通过直接积分法求解一维泊松方程基本解，与类推法得出的结果完全一致。该方法对于泊松方程基本解的学习和应用于定解问题的求解具有重要的参考价值，也有利于加深学生对格林函数的整体理解。