延胡索热风干燥特性及动力学行为

杜伟锋， 顾 超， 康显杰， 石森林， 李昌煜*， 葛卫红*

（1. 浙江中医药大学， 浙江 杭州310053； 2. 浙江中医药大学中药饮片有限公司， 浙江 杭州311401）

延胡索是罂粟科植物延胡索Corydalis yanhusuo W. T. Wang 的干燥块茎[1], 为浙八味之一, 其主要成分包括延胡索乙素等生物碱类, 具有活血化瘀、 行气止痛功效。 热风干燥[2-3]是将空气作为传递介质, 将热量传递给物料, 水分吸收热量扩散至表面, 由热空气带走的过程, 广泛应用于中药饮片的生产加工。 热风干燥技术成熟、 操作简便、 受外界影响较小, 适用于中药材产地加工。有学者对姜片[4]、 金银花[5]、 茯苓[6]等干燥过程拟合, 研究干燥特性, 建立动力学模型。 本研究采用热风干燥技术对延胡索鲜切片进行干燥, 通过研究温度和装载量对其干燥特性的影响, 建立延胡索干燥动力学模型, 为干燥工艺提供理论依据。

1 材料与方法

1.1 仪器 BWS-3-SN 电子天平（厦门佰伦斯电子科技有限公司, 精度±0.1 g）； DHZT-9070A 电热恒温鼓风干燥箱（上海精宏实验设备有限公司）。

1.2 试药 新鲜延胡索产自浙江磐安, 含水量（68.62 ± 0.25）%, 经浙江中医药大学中药饮片有限公司质检部钱敏主管中药师鉴定为正品。

1.3 样品制备 选择干燥温度（T,℃） 和装载量（L, kg/m2） 作为变量, 其中装载量为单位面积中供试品的质量。

称取新鲜延胡索切片5 份, 厚度为4 mm, 分别称取125.66、 188.50、 251.33、 314.16、 376.99 g,置于半径为10 cm 的圆形托盘中, 使其装载量分别为4、 6、 8、 10、 12 kg/m2, 分别置于鼓风干燥箱中热风干燥, 温度70 ℃, 风速恒定, 每隔20 min称定质量, 直至含水量低于15%。

称取新鲜延胡索切片5 份, 厚度为4 mm, 各称取251.33 g, 置于半径为10 cm 的圆形托盘中,使其装载量为8 kg/m2, 分别置于鼓风干燥箱中热风干燥, 温度分别为50、 60、 70、 80、 90 ℃, 风速恒定, 每隔20 min 称定质量, 直至含水量低于15%。

每组重复试验3 次, 取平均值, 采用SPSS 19.0 软件进行数据分析。

2 干燥模型及试验指标

2.1 水分测定 按2015 年版《中国药典》 “0832水分测定法” 中“第二法（烘干法） ” 测定[1]。

2.2 干基含水率 干基含水率[7-9]计算公式如下：

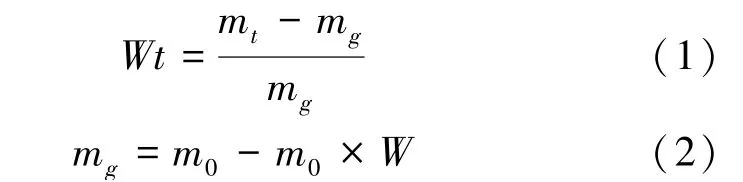
其中Wt为t 时刻延胡索的干基含水率, mt为t时刻延胡索的质量, mg为延胡索的干基质量, m0为延胡索的初始质量, W 为延胡索的初始湿基含水率。

2.3 干燥速率 干燥速率[10]计算公式如下：

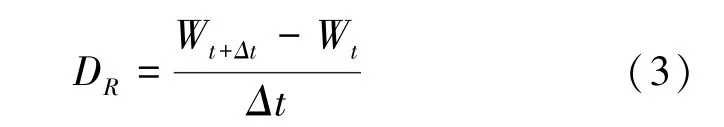
其中DR为干燥速率, Wt+Δt为t+Δt 时刻延胡索的干基含水率, Wt为t 时刻延胡索的干基含水率, Δt 为干燥间隔时间。

2.4 水分比（MR） 水分比（MR）[11]的简化计算公式如下：

其中MR 为水分比, Wt为t 时刻延胡索的干基含水率, W1为初始时刻延胡索的干基含水率数据。

2.5 薄层干燥数学模型的选取 通过文献调研,选取以下9 种常用的薄层干燥数学模型[7-10], 见表1, 该类模型适用于拟合物料质量降低只与水分蒸发相关的干燥过程。 本实验的材料为新鲜延胡索切片, 挥发性成分较少, 属于薄层干燥。

表1 常用薄层干燥数学模型Tab.1 Commonly drying mathematical model of thin layer

2.6 水分扩散系数的计算 在降速干燥阶段, 干燥过程可用费克扩散方程对其描述, 方程适用于长方形、 圆形和球形等形状的物料[12]。 假设所有的样品都有相同的初始水分分布, 对于长时间的干燥过程, 其简化方程表述如下[13]。

其中Deff为有效水分扩散系数（m2/s）, L0为样品堆积厚度的一半（m）, 取对数可得, ln MR-t 呈线性关系, 通过计算斜率可得Deff。

2.7 干燥活化能 干燥活化能为1 mol 水分子发生有效碰撞时必须具备的相对平动能的最低值, 用于描述物料干燥的难易程度。 物料在干燥过程中,水分以扩散的形式离开物料表面[12]。 其扩散系数可用Arrhenius 公式表述[14], 可以来计算活化能Ea：

其中Do为指前因子, Ea为活化能（kJ/mol）,R 为摩尔气体常量, 其数值为8.314×10-3kJ/（mol·K）,T为热力学温度（K）。 取对数可得, lnDeff-1/T 呈线性关系, 通过计算其斜率可得Ea。

3 结果

3.1 延胡索热风干燥特性 不同热风温度下延胡索的干燥速率曲线、 水分比曲线见图1～2； 不同装载量下延胡索的干燥速率曲线、 水分比曲线见图3～4。

图1 延胡索干燥速率曲线（I）Fig.1 Drying rate curves for Corydalis Rhizoma （I）

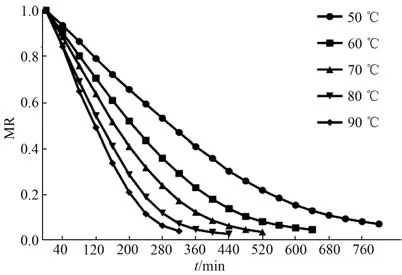
图2 延胡索水分比曲线（I）Fig.2 Moisture ratio curves for Corydalis Rhizoma （I）

由图1 可知, 在一定的温度范围内（50 ～90 ℃）, 延胡索热风干燥过程由短暂的加速干燥阶段后转为降速干燥的阶段, 初期干燥速率下降较慢, 后期干燥速度下降较快。 热风温度越高, 水分从表面蒸发的速度越快, 热风温度对延胡索的干燥速率影响显著。

由图2 可知, 随着干燥时间的延长, 不同热风温度的延胡索水分比呈下降的趋势。 初期水分比下降较快, 随后下降速度变慢并逐渐趋于平缓。 热风温度在50～90 ℃范围内, 温度对水分比的影响显著, 提高热风温度可以加速干燥过程, 可以大幅缩短干燥时间。

由图3 可知, 装载量10、 12 kg/m2的干燥速率曲线差异较小, 并有短暂的加速干燥阶段后转为降速干燥阶段, 而4、 6、 8 kg/m2的干燥速率曲线只有降速干燥阶段。 初期干燥速率下降较慢, 后期干燥速度下降较快。 装载量越小, 水分从表面蒸发的速度越快, 所以干燥速率越大, 装载量对延胡索的干燥速率影响显著。

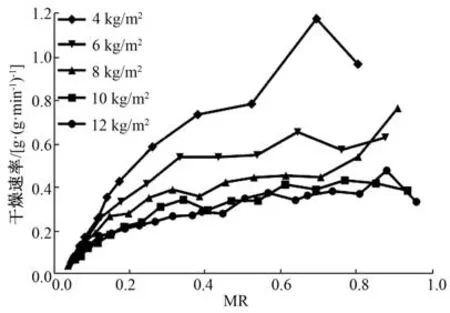
图3 延胡索的干燥速率曲线（Ⅱ）Fig.3 Drying rate curves for Corydalis Rhizoma （Ⅱ）

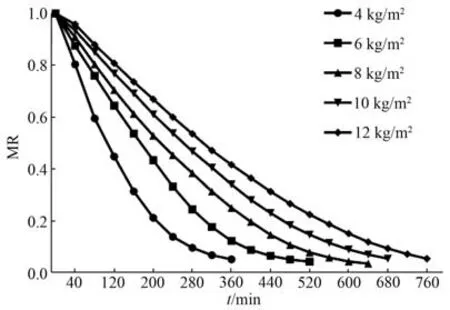
图4 延胡索的水分比曲线（Ⅱ）Fig.4 Moisture ratio curves for Corydalis Rhizoma （Ⅱ）

由图4 可知, 水分比随干燥时间延长不断下降, 干燥初期水分比下降较快, 随后下降速度变慢并逐渐趋于平缓。 装载量4 ～12 kg/m2, 装载量对水分比影响显著, 降低装载量可以加速干燥过程,大幅缩短干燥时间。

3.2 延胡索热风干燥模型的建立 以装载量8 kg/m2, 温度70 ℃为例, 用所选的9 种薄层干燥模型, 对延胡索不同热风干燥条件下的水分比曲线进行拟合, 得到各干燥模型的参数、 R2、 RMSE 和c2值, 结果见表2。

通过考察9 个模型的评价指标, 发现Page、Modified Page、 Modified Page equation-Ⅱ、 Modified Page 4 个模型的R2均大于0.999, RMSE 分别为0.007 165、 0.007 165、 0.007 165、 0.005 777, c2值分别为5.738×10-5、 5.738×10-5、 5.738×10-5、3.730×10-5, 表这4 个模型拟合程度均较高。 通过综合比较, 选择拟合曲线与实测值的差异较小, 模型评价指标R2值相对接近1, RMSE 和c2值较小,且模型参数较少的模型, 最终确定延胡索的热风干燥采用Modified Page 模型进行拟合。

表2 不同薄层干燥模型参数Tab.2 Parameters of different thin layer drying models

3.3 模型求解 由表3 可知, Modified Page 模型中的干燥常数k 随温度的升高而增加, 而n 无规律性。 k 与物质的热导性、 水分扩散性等干燥特性相关, 因此k 越大, 样品的导热效果越好, 干燥速率越快。

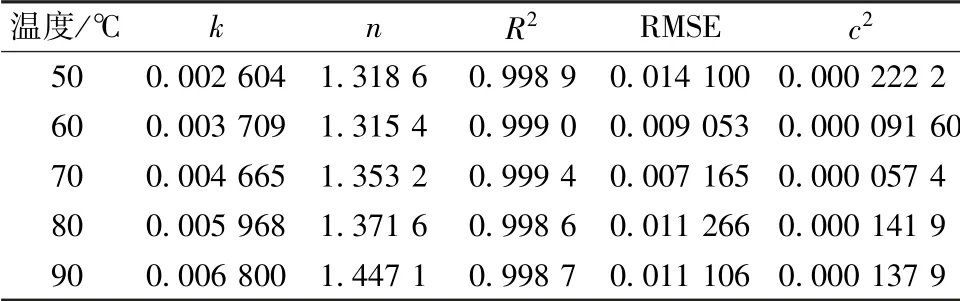
表3 Modified Page 模型干燥常数Tab.3 Drying constant of Modified Page

Modified Page 模型中的干燥常数k、 n 与延胡索的干燥温度（T,℃） 和装载量（L, kg/m2） 相关, 是关于温度和装载量的函数。 本研究采用二次多项式[5]拟合参数, 设定方程中的干燥常数n、 k的公式如下。

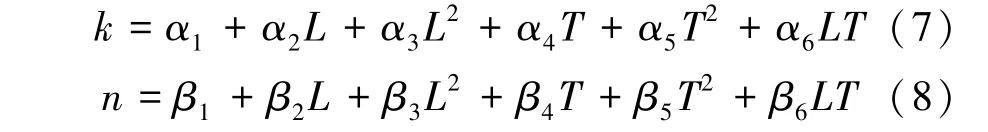
通过SPSS 软件对数据进行拟合, 求解方程中待定参数, 剔除不显著的影响因素（P＞0.05）, 得到n、 k 的回归方程, 结果如下。

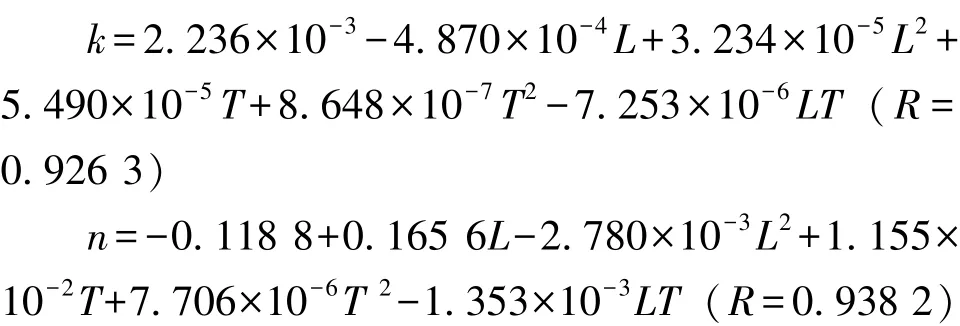
将以上各参数代入Modified Page 模型公式MR=exp [- （kt）n] 中, 得延胡索热风干燥的模型方程。

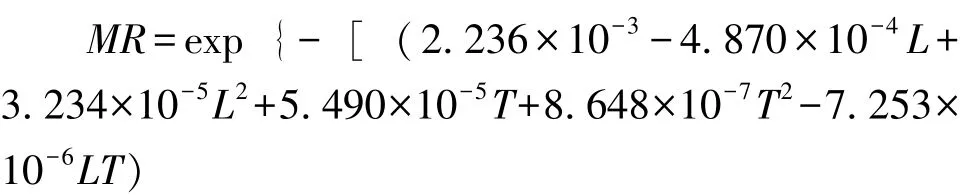
3.4 Modified Page 模型验证 为了验证模型的拟合程度, 选取装载量10 kg/m2、 干燥温度80 ℃的干燥条件, 比较水分比实测值与模型的预测值, 结果见图5。

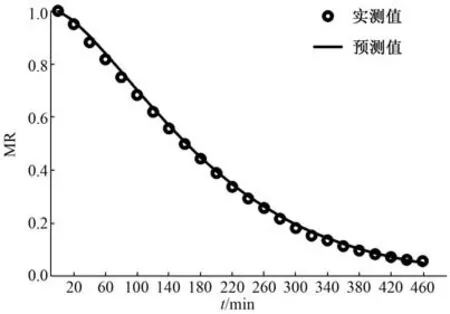
图5 实测值与预测值的差异Fig.5 Differences between measured and predicted values

由图5 可知, 在装载量10 kg/m2、 干燥温度80 ℃的干燥条件下, 延胡索水分比的实测值与预测值差异较小, Modified Page 模型可用于延胡索的热风干燥过程的预测。

3.5 有效水分扩散系数及活化能 由式（5） 可知, 延胡索饮片在干燥过程中, lnMR-t 呈线性关系[8], 通过对不同热风温度下lnMR-t 曲线的回归计算, 得到对应的水分扩散系数Deff。 由表4 可知,干燥温度在50 ～90 ℃时, 延胡索热风干燥水分有效扩散系数范围为3.972×10-10～1.362×10-9m2/s,水分有效扩散系数随着温度的升高而增大。

由公式（6） 可知, lnDeff-1/T 呈线性关系[9],根据拟合方程的斜率可以计算出延胡索热风干燥的活化能Ea。 lnDeff-1/T 的线性回归方程为lnDeff=-3 629 （1/T）-10.39, 则其活化能Ea为30.17 kJ/mol（R2=0.961 6）。

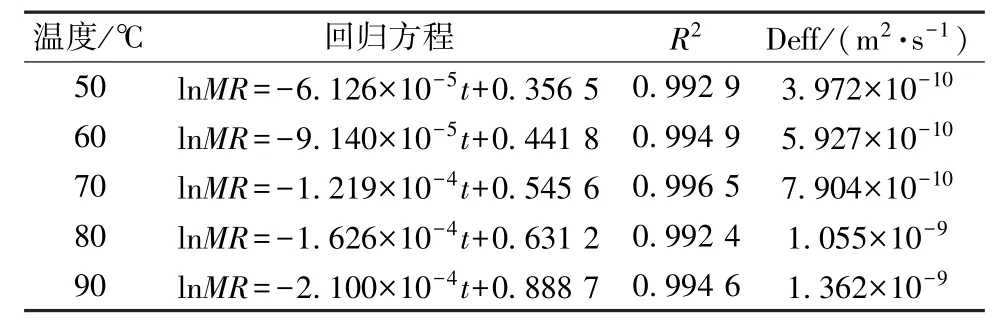
表4 延胡索水分有效扩散系数Tab.4 Effective moisture diffusion coefficient of Corydalis Rhizoma

4 讨论与结论

在装载量4 ～12 kg/m2, 50 ～90 ℃的条件下,Modified Page 模型对干燥过程的拟合度较好。 通过对模型参数的拟合, 确定参数与装载量和温度的函数关系, 建立的MR-t 函数, 能够较为准确的预测不同温度和装载量下的水分比曲线, 通过比较干燥效率, 优化干燥工艺, 建立适合的延胡索产地加工方式； 并能预测不同时刻延胡索的水分比, 用于预测延胡索干燥至预定含水量所需的时间, 减少能耗, 提高产能。

在50 ～90 ℃范围内, 延胡索热风干燥主要是降速阶段, 水分有效扩散系数随着温度的升高而增大, 范围为3.972×10-10～1.362×10-9m2/s； Ea 为30.17 kJ/mol, 在20 ～40 kJ/mol 之间[15]。 因此在延胡索热风干燥过程中, 除去的水分在固相骨架表面吸附的主要形式为物理吸附。