基于欧拉-拉格朗日模型的内燃机燃油喷雾数值模拟
2019-08-26解茂昭
李 亮,解茂昭,贾 明
(大连理工大学能源与动力工程学院,大连116024)
众所周知,喷雾的初次雾化发生在液核周边.在这一区域,流体以连续相的状态射入,气液两相之间存在强烈的相互作用,而并非离散液滴法(DDM)中所描述的以众多液体包的形式射入.而且,实验中在该区域很少发现球形的液滴,而只能观测到1个气液界面为高度褶皱的连续相流体.因此,严格地说,DDM 框架下的多种亚模型[1-3]与真实喷雾存在较大差别,且在数值模型建立过程中其对入射粒子量、喷射锥角等参数的设定具有很强的人为经验性.对喷雾近场研究比较可行的方法是连续欧拉法.此方法中,把气液界面的面积密度定义为一个函数,并导出精确的输运方程.通过输运方程的求解来描述气液界面和喷雾下游离散液滴的行为.Vallet等[4]基于这种思想,首次提出了液体射流的 ELSA(Eulerian-Lagrangian spray and atomization)雾化模型;此模型主要针对的是高雷诺数和高韦伯数的流体计算,并逐步演化出多种应用模型.
Blokkeel等[5]采用Vallet提出的方法对整个喷雾过程进行了数值研究,模拟了由近场连续相到远场离散相的转变,即假定两个液滴间的平均自由间距达到平均液滴直径的2倍时发生模型的切换,最终得出了非常满意的结果,而且当燃烧室气体密度增加时模型同样可以很精确地预测喷雾锥角的变化.Beau等[6]同样采用了均相模型,假设在液相体积分数小于 0.1时发生欧拉到拉格朗日的转换.Lebas等[7]对比ELSA模型和DNS模型的结果来确定模型的常数和参数值,并加入了蒸发模型,考虑了切应力、破碎、碰撞、汽化等因素对界面密度输运方程的影响,同时研究了不同环境气体密度、温度、射流压力等条件下ELSA模型适用性.Ning等[8]在Vallet基础上进一步增加了平衡蒸发模型,并同时修正了标准 κ-ε湍流模型,以考虑可压缩性和涡管拉伸的影响.
Belhadef等[9]通过修改界面密度输运方程中的生成和耗散项,利用欧拉均相模型对轴对称旋流喷射进行模拟,结果显示索特平均直径与实验值能很好地匹配.García-Oliver等[10]研究和验证了蒸发和无蒸发条件下可压缩Σ-Y模型,通过修改标准κ-ε湍流输运方程中的耗散系数,可以精确地预测不同入射压力和环境气体密度下液体和喷雾的贯穿距、轴向速度和混合质量分数分布.而且,随着环境气体密度和入射压力的增加,预测精度也相应增加.
从先前的研究可见,欧拉-拉格朗日模型在喷雾中的应用相对较少.本文在先前基于 OpenFOAM 所构建的欧拉模型[11]的基础上,参照Vallet理论和前人的研究,构建欧拉-拉格朗日模型.在Vallet的最初模型中,压力是通过状态方程直接求解[4];在当前构建的模型中,则采用 PISO算法来迭代求解压力泊松方程.由于该模型假设液相向气体环境的弥散主要是由湍流扩散控制,故湍流模型的选择将对计算产生影响.因此,本文对动量方程分别进行了RANS和LES封闭,以考察湍流模型的影响,其中RANS封闭模型见文献[11].最后,应用此模型对柴油喷射特性进行数值研究,模拟对象为 ECN(engine combustion network)喷雾 A[12]2106753#试验,此喷雾已广泛应用于发动机各种喷雾模型的验证.
1 理论模型
Vallet等[14]在 1998年提出了一种新的欧拉喷雾计算模型,此模型中同样包含对离散液滴相的求解;因此,也可被称作欧拉-拉格朗日模型.此模型的基本出发点是:高雷诺数和高韦伯数的高速液体湍流射流的雾化过程,与具有大密度差的气体射流的湍流混合过程非常相似.从计算的观点看,Vallet模型把喷雾视为液体和气体混合物组成的一种单一的“有效流体”.液相向气体环境的弥散主要是由于湍流扩散控制;对于小尺度的离散项,则通过一个局部的液体质量分数以及气液界面面积密度值来描述;此二者的值则通过求解其各自的输运方程得出.
事实上,喷雾实验中发现在喷嘴的出口存在一个连续的界面高度褶皱的液核,燃料的初次雾化发生在液核周边,2次及多次雾化则在喷射的相对下游.正是基于这一现实,Vallet模型在接近喷嘴的稠密区采用欧拉方法描述气液两相行为,而在喷嘴下游的稀薄区则采用拉格朗日方法来描述.
模型中,欧拉相的基本控制方程的求解是采用均相模型方式,详细表达式见笔者前期研究[11].湍流求解本文采用 LES方法,其中亚格子模型选用单方程湍动能模式,模型具体的描述见文献[13].模型中两相混合物密度按式(1)计算[4]:

式中:Y是当地液相质量分数,Y=1为纯液相,Y=0为纯气相;ρl,ρg分别为液、气相密度.气相密度采用理想气体状态方程求解,液相密度采用线性的可压缩方程求解.

其中φl,p0分别为液相可压缩常数和初始参考压力.
模型中质量分数的输运方程为
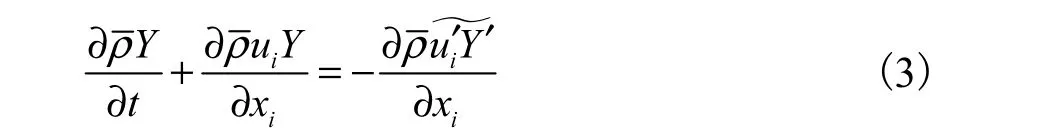
方程右侧为液相的湍流扩散,即湍流引起的液、气相之间的质量弥散;其可由 Demoulin[14]模型进行封闭:
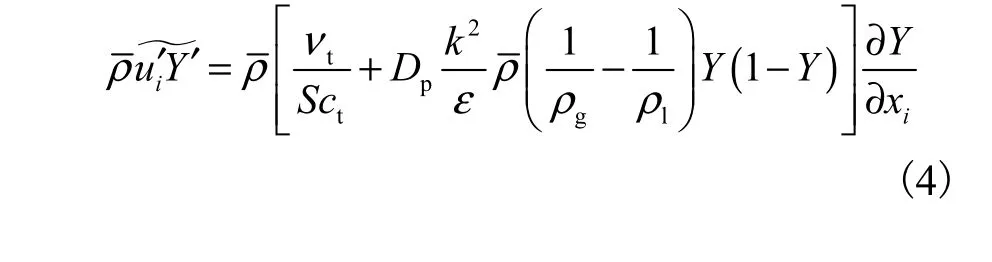
其中 Sct,Dp分别为 0.9 和 1.8.
对于拉格朗日离散相特性,需要借助气液界面面积密度输运方程[4]进行求解.具体方程如下:
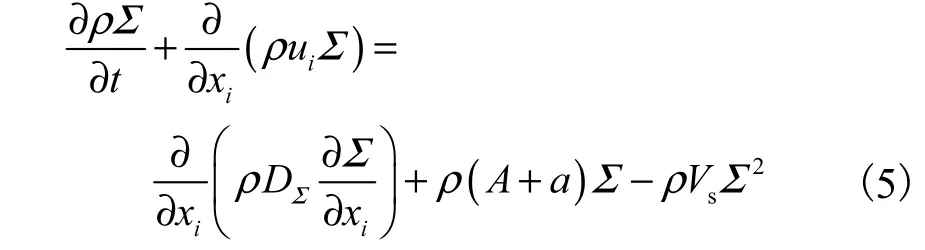
此界面面积密度(Σ)则代表了每一个网格单元中液相的分裂程度的亚网格信息.输运方程推导过程则采用了与火焰面密度输运方程类似的方法;其中,方程右侧的源项,考虑了表面张力、湍流拉伸、液滴碰撞和聚结等因素的影响.方程中各相关变量的含义如下:
DΣ为一扩散系数,其值等于湍流黏性除以施密特数.

A为由于平均速度梯度引起的气液界面的拉伸生成项即

a为考虑液滴破碎和碰撞而引起的界面的生成项,即

Vs为液滴碰撞和聚结引起的界面的耗散项:

式中:req为湍流特征时间尺度(lt)内面密度达到平衡值时对应的液滴的平衡稳定半径,即
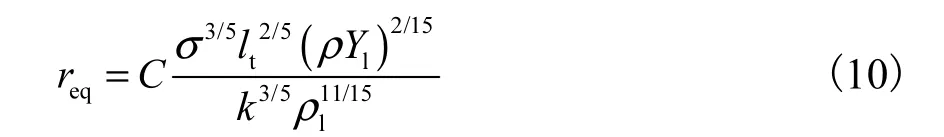
拉格朗日液滴的尺寸和液滴数通过当地的液相质量分数和界面面积密度来确定.具体如下:

2 物理模型及定解条件
由于计算模型中没有考虑蒸发作用,因此选择的试验模型同样也是低温下的ECN Spray A 21067[12],试验条件详见表 1.物理模型为圆柱体,长 80mm,直径 50mm,喷嘴的直径为 89.4µm.网格划分为六面体正交网格,采用两套网格系统进行无关性检验.网格划分方面,喷嘴处沿径向均匀划分为 16个节点;腔室沿轴向和径向按比例因子为 1.01、1.06划分为300和200个节点,网格总量为300万.
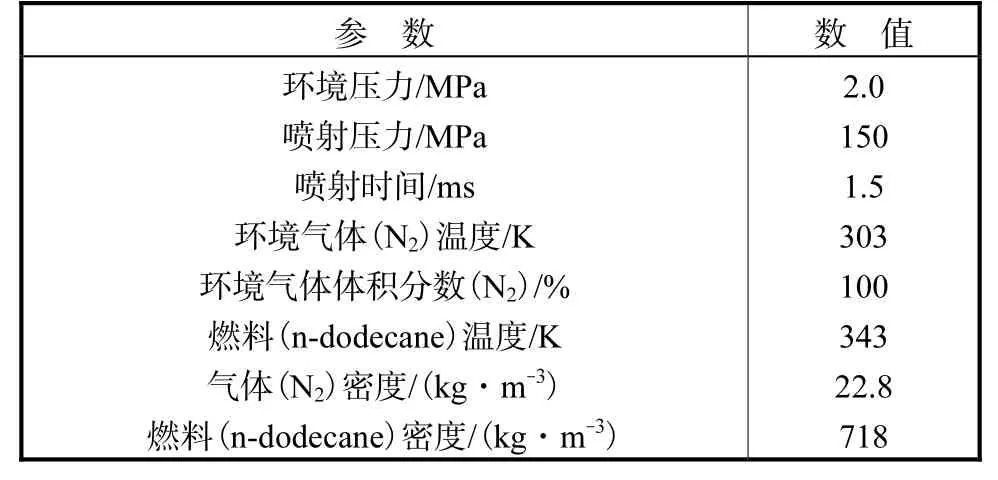
表1 实验参数Tab.1 Experimental parameters
壁面采用无滑移绝热壁面;出口为第 2类边界,无回流;入口为第1类边界,入口速度随时间变化.
插值格式方面,时间项采用 1阶 Euler隐式格式;对流项选用 Gauss Gamma差值格式;Laplacian项选用 Gauss linear corrected差值;梯度项为Gauss linear差值;其中,面法向梯度需进行非正交修正.
3 结果分析
由于ECN[12]实验所得的数据和云图是1.4ms以内平均值;因此,此处的定性分析云图和下面的定量分析数据需要将喷射时刻 1.5ms以内的大涡模拟数据进行取样平均(见图1).体积分数与质量分数的转换如下:


图1 喷雾质量分数Fig.1 Mass fraction of spray
首先对喷雾中的欧拉特性进行分析.图2反映了稳定喷射后、轴距6mm以内的燃料体积分数与实验的对比.其中,实验图片为 ECN所得,详见文献[15].对比实验图片发现,在 3mm 内模拟的预测结果较好,只是在末端附近模拟结果高于实验值.然而,在 3~6mm 内两者的偏差增大,尤其是在轴距3mm 附近,实验云图的峰值较大,模拟值过低地预测了轴心燃料分布;然而,在下游6mm附近,轴心处的模拟结果显示了比实验值更高的体积分数.

图2 轴向体积分数Fig.2 Axial volume fractions
对于离散相的分布,图3和图4分别给出了t=0.5ms时刻粒径D32和粒子量N的分布云图.从图3可见,在轴线处粒子直径沿喷射方向先减小,后又逐渐增大.由此证实在喷嘴出口附近,由于气液剪切和湍流作用,使得射流发生分裂破碎,粒径减小、粒子量增加.同时,由图3可见,在喷雾的径向边缘和末端下游附近,粒子的直径较大;其增大的原因可能是在上述区域存在更为剧烈的气液剪切作用和湍流扰动,造成液滴间的碰撞聚合作用加剧.对应于图4中的变化,是粒子量在喷雾下游减小.因此,可以认为在喷雾的下游,由于流速和湍流扰动的下降使得粒子间的碰撞融合加剧,从而导致粒径的增加和粒子量的减小.而且,由图4可见粒子量分布则是沿轴向先增加后减小,这与D32的整个云图的分布正好相反.
图5直观地给出了两相界面面积密度值的分布云图.由喷嘴附近的放大云图可见,在喷嘴出口附近,界面面积密度值接近于零,可以间接证实喷嘴出口附近射流液核的存在.同时,由于界面面积密度值代表的是当前计算单元的液相的分裂程度,即其值越大说明此单元网格内的分裂雾化效果越有效,平均液滴直径越小;反之,其值越小,平均粒径越大.因此,从图5分布也可说明,在靠近液核的下游,液相的分裂雾化更强,产生的粒子直径更小;然而,在喷雾的边缘和下游,其分裂下降,粒径增加,使得界面面积密度值减小.此结果与图3的粒径分布对应;而且,在喷嘴出口的液核周边,初次破碎的气液界面为一种连续褶皱形态,且沿轴向逐渐向轴线收缩.

图3 粒径D32分布云图Fig.3 Nephogram of D32
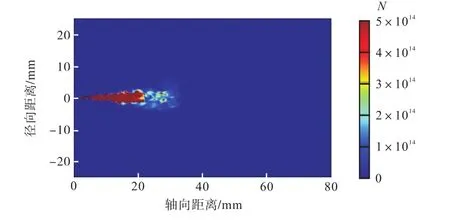
图4 粒子量N分布云图Fig.4 Nephogram of the number of droplets N

图5 两相界面面积密度∑分布云图Fig.5 Nephogram of two-phase interfacial area density
图6给出了不同喷射时刻喷雾的贯穿距与实验值对比;其中,RANS模型为利用两相密度修正后的湍流模型[11].对比RANS模型和实验数据发现,在喷雾的初始时刻,LES模型具有更长的贯穿距;然而在0.2ms之后,即喷雾达到稳定喷射后,LES与实验结果更加吻合.
图7显示了轴心线的燃料体积分数分布.在喷嘴附近,LES模拟与实验对比显示了良好的发展趋势;而且,展现了喷嘴出口处稳定完整液核的存在;同时,实验值的体积分数保持在 0.9上下波动,这可能与实验中喷嘴内部的气穴现象或者周围的湍流气相卷吸有关;然而,在本文的模拟中并没有考虑喷嘴内的空化因素.
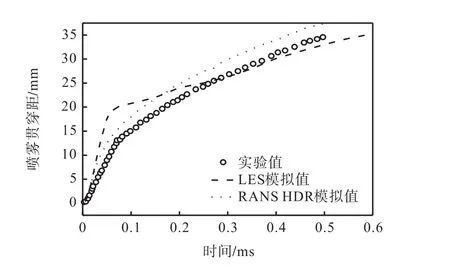
图6 喷雾贯穿距Fig.6 Spray penetrations
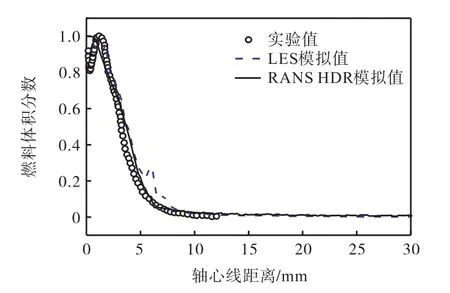
图7 喷雾轴线体积分数分布Fig.7 Distribution of volume fractions on the axis
在液核下游燃料的体积分数迅速衰减,LES和RANS模型均很好地捕捉了此衰减过程;但是,LES在轴距 6mm附近却存在一个明显的小峰值;这说明LES的衰减过程中在此处存在燃料的部分聚集,这与图2的结果相对应.
为了进一步分析喷嘴出口附近RANS和LES结果的不同,图8给出了轴向速度分布.由图可见,LES在6mm内的高速度值区间较RANS结果更长,尤其是在6mm处出现一个小的速度峰值;这对应于LES模拟 6mm附近燃料分布的波动.此后,LES模拟的速度下降速率过快,速度值低于 RANS模拟结果,这使得 LES模型喷雾末端的喷雾贯穿距低于RANS模型的预测结果.

图8 喷雾轴心线速度分布Fig.8 Distribution of axial velocity in the spraying process
图9对不同横截面处体积分数的径向扩散分布进行对比验证,由于图2、图7显示预测值与实验值的差别主要位于轴距 6mm 内.因此,分别选取轴距为 0.1mm、2mm和 6mm 共 3个不同轴向位置.在轴距 0.1 mm 处,由于位于喷嘴出口处存在液核,体积分数在液核边缘存在断崖式下降;通过对比实验值可见,LES的结果与边缘体积分数的下降趋势吻合较好;然而,RANS结果则呈现出更加尖锐的断崖式变化.同时,在中心的液核区,LES的预测结果同样与实验测量值更接近;然而,RANS结果略微偏高;同时,在轴心处的 RANS模型曲线的水平线性的跨度更宽.在轴距 2mm 处,同样在体积分数下降的径向边缘,LES的结果与实验值更接近;然而,在轴线处,LES的预测值略高;RANS的预测值略低.对于轴距6mm 处,虽然 LES在径向边缘处的预测较好,但是在轴心处的狭小区间内却存在过高的体积分数,其值大约为实验值的 2.5倍;然而,RANS的预测值虽然在径向边缘略高,但在轴心处与实验值更吻合.
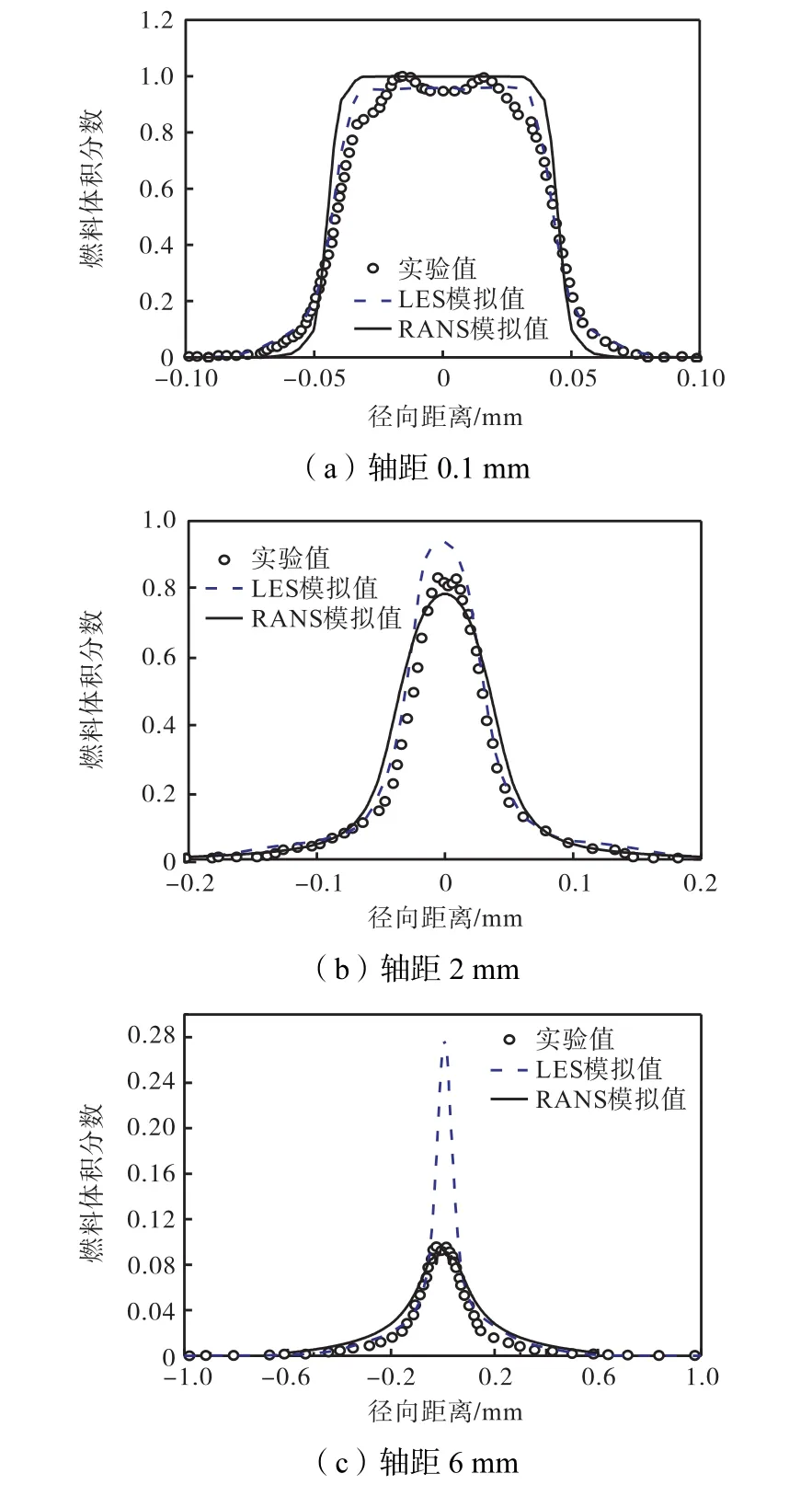
图9 燃料体积分数的径向分布Fig.9 Radial distribution of volume fractions
为了直观地显示和分析 LES模拟值在此处出现较高体积分数值的原因,图10给出了燃料1.5ms时刻的瞬时质量分数、涡量云图,以及整个喷射时间平均化处理后的质量分数、涡量云图.由图可见,LES模拟的喷雾在 6mm附近存在高的质量分数和强的涡量分布.而且,此处的不稳定波动增强,促使喷雾产生初次分离和破碎,形成高密度液体包;由公式(12)知,质量分数与体积分数相对应,同时,考虑到高密度梯度对射流的流体动力学稳定作用,即所谓固壁效应,使得射流的进一步不稳定性破碎产生延迟.然而,一旦失稳发生,大的稠密的流体包裹将再次分离破碎,产生快速移动的块状结构或韧带,增强了射流末端的局部湍流和不稳定波动,从而对气液混合产生显著影响,进而影响体积分数的分布.
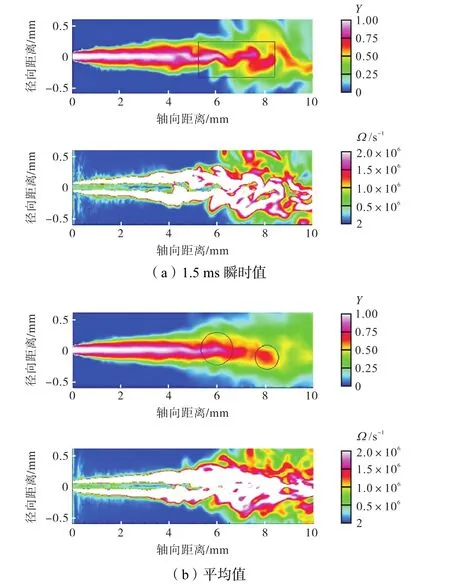
图10 LES模型给出的燃料质量分数Y和涡量Ω 分布云图Fig.10 Nephograms of mass fraction and vortices given by the LES model
图11给出了喷雾D32随喷射时间的发展变化和分布.随着时间的发展,喷雾的下游和边缘的液滴直径逐渐增大,液滴的大直径范围也逐渐增加.图12给出了平均化处理后的不同轴距处 D32的径向分布,同时与García-Oliver的实验进行对比.图12(a)显示在喷雾的下游,液滴直径的径向分布沿轴向逐渐增加;同一径向曲线的最大液滴直径均位于喷雾的径向边缘.图12(b)中García-Oliver实验条件为喷射压力80MPa,环境密度ρ为 10~40kg/m3;本文中的模拟算例的喷射压力为 150MPa,环境密度为 22 kg/m3;由实验数据可见,随着环境密度的增加,液滴径向的直径逐渐增加,直径径向的分布也更加均一.对比实验值与模拟曲线可见,本文和 García-Oliver的模拟值均小于测量值.在保证环境密度值近似的条件下,相同轴距处,本文模拟的液滴直径较 García-Oliver的模拟值更小,径向分布更宽;这是完全正确的,因为高的喷射压力必然导致高的流速和湍流强度,液滴的分裂破碎加剧,产生较小的液滴直径.
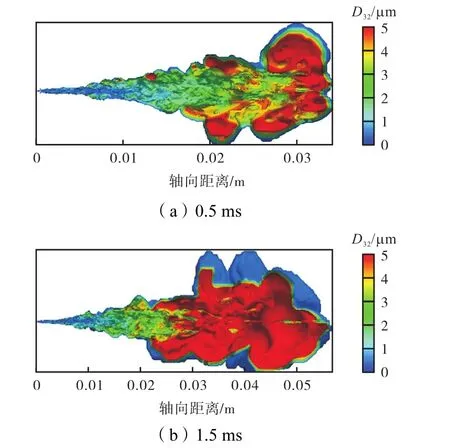
图11 轴向D32外部轮廓Fig.11 Exterior profile of axial D32

图12 D32的径向分布Fig.12 Radial distribution of D32
4 结 论
(1) 对于喷雾中的欧拉特性,除了在轴距 6mm附近轴心线的体积分数的实验值存在一定差别外,LES模拟的预测值与实验吻合较好,尤其是燃料的径向分布;同时,也可以捕捉到喷嘴出口附近恒密度液核的存在.对于轴距 6mm 处的偏差,这与大涡模拟下此处高的质量分数和涡量分布有关,使得液核末端不稳定波动产生高密度的液体包,这些高密度液体包的进一步破碎受到气液密度差的抑制而产生延迟,进而影响液核末端的体积分数分布.
(2) 对于离散相而言,在喷嘴出口处粒子直径基本等同于喷嘴直径;而且,界面面积密度值接近零,这进一步证实了喷嘴出口连续液核的存在.同时,由于界面面积密度值可表征液体的分裂程度,因此,由其分布可知:在液核末端的下游,液相的分裂破碎增强,产生较小的粒子直径;而在喷雾的下游,液滴粒子间的碰撞融合加剧,使得液滴直径略显增加.对比液滴直径实验值与模拟值可见,相同轴距处,本文模拟的液滴直径较小,径向分布较宽,这与高的喷射压力直接相关.
