基于零序电流积分的单相接地故障定位方法
2019-08-24闫丽梅张琰骏徐建军
闫丽梅,张琰骏,徐建军,杨 帆
(东北石油大学电气信息工程学院,黑龙江 大庆 163318)
0 引言
35 kV及以下电压等级的线路称为配电线路。配电线路易发生各类短路故障,其中单相接地故障的比例高达70%。目前,已存在多种单相接地故障检测和定位方法。各方法根据所利用信号的不同,分为暂态法[1-2]和稳态法;根据原理的不同,分为注入法[3]、相似性法[4]等;根据定位范围的不同,有故障测距法和区段故障定位[5-7]等。常见的一些定位方法存在故障信号获取复杂的缺点。相似性法存在数据计算量大、通信成本高的缺点。一些先进数学算法已应用到电力系统故障定位上(如小波变换、神经网络和模式分析)[8-10]。这些方法故障特征计算准确,但原理和算法复杂、计算量大。
为研究一种故障信号获取方便、原理简单、数据计算量和通信传输成本小的方法,本文提出基于零序电流分时积分原理的故障定位方法。借助Matlab/Simulink搭建10 kV配电网模型,对不同故障情况下的单相接地故障进行仿真验证。验证结果表明,该方法定位准确,高阻接地、线路末端接地和电弧性接地的适用性好。
1 单相接地时零序电流故障特性
某配电网单相接地故障后的系统等效零序网络结构如图1所示。其中:f为故障点,;M、N、P、Q为故障线路检测点;RL、jXL为站内消弧线圈等效阻抗;C01、C02、C03为线路L1、L2、L3对地电容;C1、C2、C3、C4为L4线路MN、NF、FP、PQ区段的对地电容[11]。

图1 系统等效零序网络结构图Fig.1 Equivalent zero sequence network structure of system
假设L4线路NP区段上的f点发生单相接地故障。此时,故障区段NP两侧N点和P点流过的零序电流存在以下关系:
i0N=i0M+iC1
(1)
i0P=i0Q+iC4
(2)
式中:i0M=i01+i02+i03为健全线路对地电容电流之和;iC1为MN区段对地容性电流;i0Q为流经Q点的对地容性电流;iC4为PQ区段对地容性电流。
通常配电网一条母线下存在多条出线,使得故障点前零序电流远大于流经故障点之后的零序电流[12],即i0N>>i0P。
根据线路结构,M点和N点流过的零序电流存在如下关系:
i0M=i0N-iC1
(3)
通常情况下,MN区段设置线路距离较短。因此,其对地电容电流iC1要远小于非故障线路对地电容电流的之和i0M,可忽略[13]。即:
i0M≈i0N
(4)
P点和Q点流过的零序电流存在如下关系:
i0Q=i0P-iC2
(5)
即P、Q点检测到的零序电流也近似一致。
综合上述分析,单相接地时故障线路上各检测点零序电流具有以下特性:故障点之前(或之后)同侧相邻检测点流过的零序电流波形相似,幅值差别小;故障点前后两侧检测点流过的零序电流波形差别大,幅值差别大。
2 零序电流幅值分段积分定位方法
2.1 定位原理
对于存在6个检测点的某条线路,在3、4检测点之间发生的单相接地故障如图2所示。
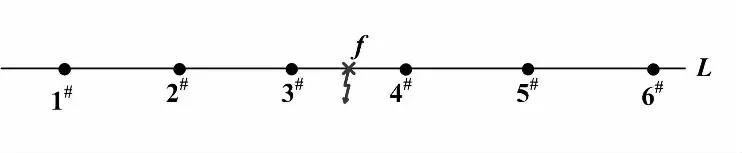
图2 故障示意图Fig.2 Schematic diagram of fault
暂态零序电流波形如图3所示,其对应幅值分布曲线如图4所示。

图3 暂态零序电流波形Fig.3 Waves of transient zero sequence current
图3、图4验证了上文对单相接地故障发生后暂态零序电流故障特性分析。
为体现暂态零序电流幅值特征,对故障发生后两个周期内暂态零序电流按时段计算幅值,得到各检测点零序电流幅值序列。各时段暂态零序电流幅值为:
(6)
式中:m为时段,m=1,2,…,8;I0(m)为第m个时段内暂态零序电流幅值;n为第m个时段内暂态零序电流数据采样数;i0t为暂态零序电流。
为计算不同检测点间的零序电流幅值差异,定义幅值积分系数E为:
(7)
式中:E(I1,I2)为幅值积分系数;I01(k)、I02(k)为2个检测点的故障暂态零序电流幅值序列。
I01={I01(1),I01(2),I01(3),I01(4),I01(5),
I01(6),I01(7),I01(8)}
I02={I02(1),I02(2),I02(3),I02(4),I02(5),
I02(6),I02(7),I02(8)}
线路出现单相接地故障时,故障线路上非故障区段两端检测点暂态零序电流幅值接近,幅值积分系数小。故障区段两端检测点流过的暂态电流幅值存在明显差异,幅值积分系数大。因此,可根据幅值积分系数判定故障区段。其定位判据为:故障区段为所计算暂态零序电流幅值积分系数最大值的区段。
一次线路末端发生单相接地时,故障暂态零序电流波形如图5所示,其对应幅值分布曲线如图6所示。由图5和图6可知,线路末端发生单相接地时,整条故障线路上相邻检测点之间的零序电流波形相似度高,各区段计算所得幅值积分系数差别小。
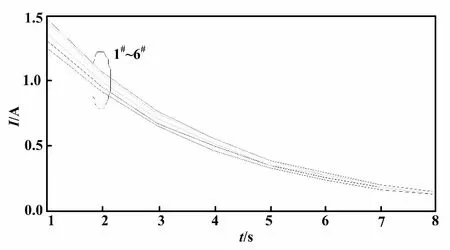
图6 故障暂态零序电流分时段幅值分布曲线(1#~6#)Fig.6 Time-divisional amplitude distribution curves of fault transient zero sequence current(1#~6#)
为此,以定义幅值积分差异系数表示各区段计算所得零序电流幅值积分系数之间的差异性。若幅值积分差异系数小于所设定阈值,线路末端发生单相接地故障。定义幅值积分差异系数δ为:
δ=Emax-Emin
(8)
式中:δ为幅值积分差异系数;Emax为故障线路各区段幅值积分系数最大值;Emin为故障线路各区段幅值积分系数最小值。
2.2 定位流程
本文仿真中设定阈值δset=0.1。该值可由现场实际和采样检测设备的精度设定。定位算法流程如图7所示。
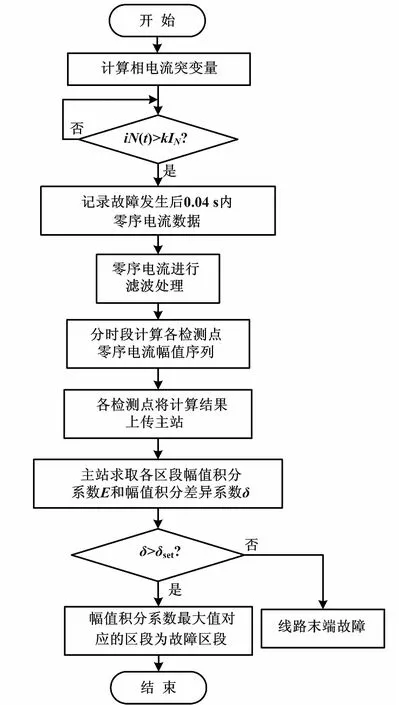
图7 定位算法流程图Fig.7 Flowchart of positioning algorithm
3 仿真验证
利用Matlab/Simulink搭建10 kV配电网仿真模型[14]。仿真示意图如图8所示。

图8 仿真示意图Fig.8 Simulation diagram
仿真中,线路总长度为44 km。其中:L1=10 km,L2=10 km,L3=13 km,L4=11 km。架空线路的正序参数R=0.17 Ω,L=1.2e-3 H,C=9.697e-9 F;零序参数R=0.23 Ω,L=5.48e-3 H,C=6e-9 F。
3.1 一般性接地故障分析
L4线路设置以下3种故障情况,对设计算法的准确性进行仿真验证。故障情况1:故障点位于[1,2]区段。故障情况2:故障点位于[3,4]区段。故障情况3:故障点位于[5,6]区段。分别对不同故障初相角和不同接地过渡电阻进行仿真,设置采样频率为20 kHz,选取故障发生后0.04 s内数据进行计算处理。
一般性接地故障数据处理结果如表1所示。

表1 一般性接地故障数据处理结果Tab.1 Processing results of general grounding fault data
注:故障1、3、5为故障区段,Rf为接地电阻,E[1,2]~E[5,6]为幅值积分系数,δ为幅值综合差异系数
由表1可知,当线路区段1,3,5发生单相接地故障时(故障区段为[1,2]、[3,4]、[5,6]),计算得到的幅值综合差异系数δ值远大于δset=0.1,且故障区段的暂态零序电流幅值积分系数值E均最大,远大于非故障区段暂态零序电流幅值积分系数,定位准确。
3.2 线路末端接地故障分析
为验证所设计算法对线路末端接地故障情况的适应性,设置线路L4末端发生不同接地电阻和故障初相角下的单相接地故障,对算法进行仿真。
线路末端接地故障数据处理结果如表2所示。

表2 线路末端接地故障数据处理结果Tab.2 Processing results of grounding fault data at the end of the line
由表2可知,当单相接地故障出现在线路末端时,各区段计算的幅值积分系数接近。此时计算得到的幅值综合差异系数δ值远大于δset=0.1,确定为线路末端故障,定位准确。
3.3 电弧性接地故障分析
在配电网发生的单相接地故障中,有很大比例为电弧性接地故障。为了验证设计的定位原理和算法对电弧性接地故障的通用性,建立Cassie电弧模型[15-16],将该电弧模型加入到单相接地故障模块中,进行仿真验证。电弧性接地数据处理结果如表3所示。
由表3可知,当线路区段2,4发生电弧性单相接地故障时,计算得到的幅值综合差异系数δ值远大于δset=0.1,且故障区段的暂态零序电流幅值积分系数值E[2,3]、E[4,5]均最大,远大于非故障区段暂态零序电流幅值积分系数,定位准确。当线路末端发生电弧性接地故障时,计算得到的幅值综合差异系数δ值远小于δset=0.1,确定为线路末端故障,定位准确。
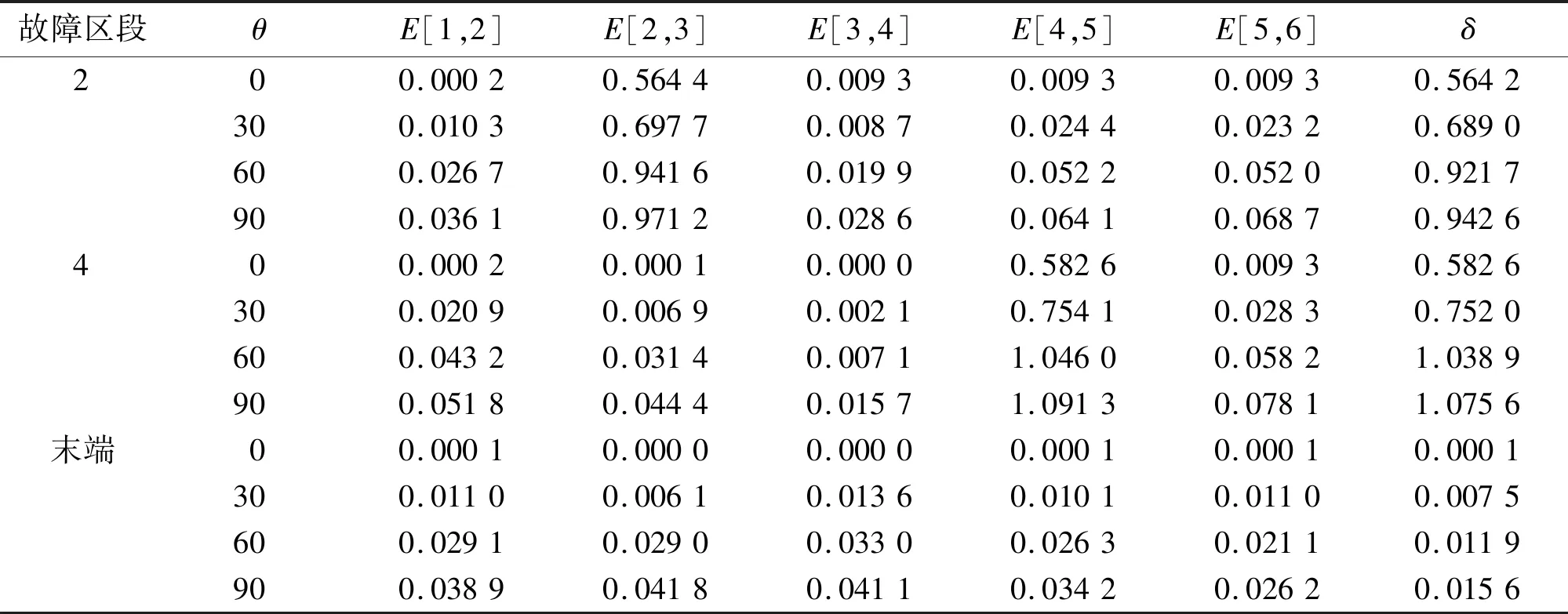
表3 电弧性接地数据处理结果Tab.3 Processing results of arc grounding data
4 结束语
本文根据单相接地故障发生后的故障零序电流,分区段计算各段零序电流幅值积分系数,并利用幅值积分系数进行故障定位。该方法具有信号获取方便、计算量小的特点,对不同故障条件下的单相接地故障下定位准确度高,在高电阻接地、末端接地以及电弧性接地故障时适用性好。该研究为配电网单相接地故障定位提供了一种新的方法。
