区域集中供热室温控制策略研究

朱冬雪，褚红燕，林福建，鹿世化

(南京师范大学能源与机械工程学院，江苏 南京 210042)

0 引言

近年来，集中供热系统在我国北方地区[1]应用广泛，但在系统运行过程中出现了许多问题[2]，如热量利用率不高[3]、系统自动化水平不高[4]、热计量技术水平低和统计预测能力不强等，造成了采暖用户室内温度不均、热量损失严重。这些问题对供热系统的稳定运行产生了很大的影响。

目前，国内外研究学者对区域集中供热系统中的常用控制方法有前端控制和末端控制。文献[5]针对太阳能集热器蓄热效果欠佳的问题，设计了一种通用集热器，对太阳能集热器的热量采集进行实时控制，满足冬季集中供热系统热量的需求。文献[6]针对热交换站能耗高、效率低的问题作出相关的研究。在原有的换热器上添加一个备用换热器，对换热器进行合理的协调控制，满足了供热系统中的供热需求。文献[7]对塔林地区供热管网热量损失问题作了相关研究。通过管网的监测系统，对管道进行改进，以保证末端用户的需热量。文献[8]针对集中供热系统末端用户冷热不均的问题，设计了一种远程阀门控制系统。在室内放置一个温度传感器来监测室内温度，通过无线通信技术来控制阀门的开度。由于缺乏试验验证，无法准确判断在阀门开度调节过程中的系统稳定状态。

以上学者的研究使得供热系统中热量损失大大降低，但实际采暖时用户室内温度不能稳定在舒适的阈值范围内。本文采用一种高效的室内供热系统建模方法和控制算法，设计了合理的室内温度控制器，使室内温度快速稳定在温度阈值范围内，保证供热系统的节能、稳定运行。

1 室内供暖系统建模

本文对郑州地区某住宅小区冬季区域集中供热采暖出现的冷热不均问题进行了深入研究。为了更好地实现区域集中供热末端用户用热需求，设计了散热器的闭环供热系统，对室内温度供热系统进行数学建模。

室内温度供热系统数学模型如图1所示。

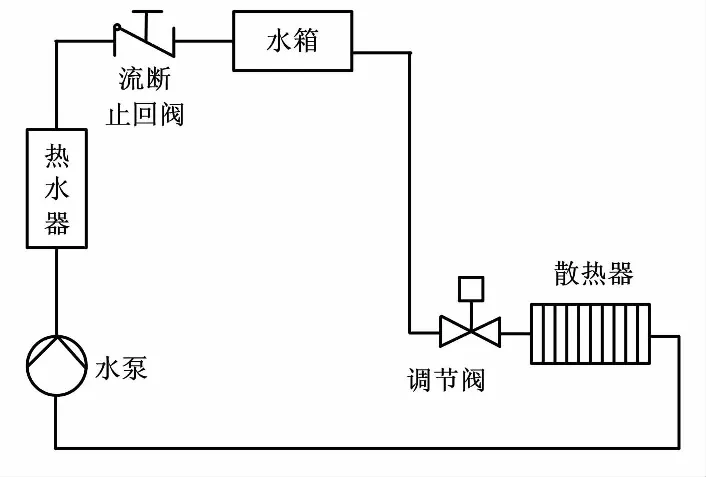
图1 室内温度供热系统数学模型Fig.1 Mathematical model of indoor temperature heating system

储热水箱动态方程为：

(1)

式中：K为阀门流量系数；μ为调节阀的开度；h为水箱水位高度的变化值；R为出口阀门阻力；A为水箱截面积。

对于散热器近似动态模型[9]来说，能量的转换公式为：

Q1=G1CPT1ρ

(2)

式中：Q1为水进入散热器所带的热量；CP为热水的比热容；T1为进口热水的温度；ρ为热水密度。

Q2=G1CPT2ρ

(3)

式中：Q2为水流出散热器所带的热量；T2为出口热水的温度。

散热器与表面空气对流换热的热量为：

Q3=h1A1(TW2-Tf)

(4)

式中：Q3为散热器与表面空气对流换热的热量；h1为散热器与表面空气对流换热的换热系数；A1为散热器表面的面积；TW2为散热器表面的温度；Tf为房间空气的温度。

Q4=h2A1(TW2-Tf)

(5)

式中：Q4为散热器与表面空气辐射所散失的热量；h2为散热器与表面空气对流换热的换热系数。

散热器自身贮存的热量为：

(6)

式中：Q5为散热器贮存的热量。

散热器中传递的总热量为：

Q1-Q2=Q3+Q4+Q5

(7)

整理公式可得：

(8)

化简式(8)，作适当优化和拉氏变换，可得：

(9)

通过查阅相关资料，把已知数据代入式(9)。室内温度供热系统传递函数为：

(10)

2 误差反向传播神经网络PID控制器

2.1 改进的单神经元自适应PID控制器

常规PID控制器只能对一些线性系统作出简单的控制，以达到稳定、高效的目的。而对于一些非线性、大时滞、多变量的系统来说，传统PID控制器的控制效果极其不稳定。这时，采用改进的单神经元自适应PID控制器[10]对系统的运行作出调整，使其系统能够稳定运行。改进的单神经元自适应PID 控制器结构如图2所示。

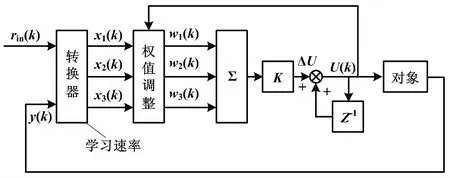
图2 改进的单神经元自适应PID 控制器结构图Fig.2 Structure of improved single neuron adaptive PID controller

图2中：rin(k)为输入信号、y(k)为系统输出信号；经过转换器之后，输入、输出信号转换成神经元的输入量x1(k)、x2(k)、x3(k)；wi(k)为神经元输入量的加权系数；z(k)为系统的性能指标；K为神经元的比例系数。

本文选择K>0，每个神经元之间通过权系数的自我调整来实现系统的自我学习功能。改进的单神经元自适应PID学习算法如下。

(11)

x1(k)=e(k)

(12)

x2(k)=Δe(k)=e(k)-e(k-1)

(13)

x3(k)=Δ2e(k)=e(k)-2e(k-1)+e(k-2)

w1(k)=w1(k-1)+ηiz(k)u(k)[e(k)+Δe(k)]

w2(k)=w2(k-1)+ηpz(k)u(k)[e(k)+Δe(k)]

w3(k)=w3(k-1)+ηdz(k)u(k)[e(k)+Δe(k)]

式中：ηp、ηi、ηd分别为比例系数、积分系数、微分系数学习速率，一般取0<η<1。

2.2 BP神经网络PID控制器

改进的单神经元自适应PID控制器对于非线性系统控制性能良好，自我调节能力强。基于神经元之间信号传递强、传输速度快的特点，提出了神经网络的构想。BP神经网络控制器中各个神经元之间相互联系结构和电网一样，可以实现信息的快速传递。BP神经网络的基本模型是一个三层前馈网络，包括输入层、隐含层和输出层，各层之间权系数连接。根据对象的复杂程度，选择适当的网络结构，就可以实现从输入空间到输出空间的任意非线性函数[11-12]的映射。

在设计BP神经网络结构时，有以下两点需要考虑。首先是隐含层的数量,其次是隐含层节点的数量。研究表明，有两个隐含层的神经网络可以解决任何类型的分类问题。但后来许多研究学者指出，只要有一个隐含层的神经网络包含足够多的节点，就能以任意的精度逼近非线性函数，对系统进行精确的控制。

BP神经网络基本结构如图3所示。

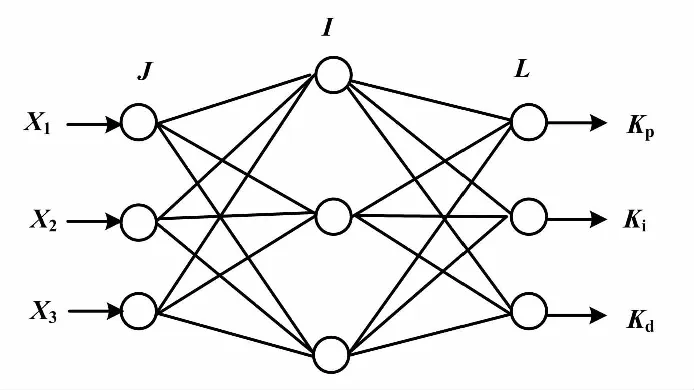
图3 BP神经网络基本结构图Fig.3 Basic structure of BP neural network

BP神经网络输入层变量为：

(14)

BP神经网络隐含层的输入、输出变量分别为：

(15)

(16)

式中：w(2)ij为隐含层加权系数；上角标(1)、(2)、(3)分别为输入层、隐含层和输出层。

隐含层神经元的活化函数取正负对称的Sigmoid函数：

(17)

BP神经网络输出层的输入、输出变量分别为：

(18)

(19)

(20)

(21)

(22)

BP神经网络输出层输出变量kp、ki、kd不能为负值。因此，取输出层神经元的活化函数为非负的Sigmoid函数：

(23)

取性能指标函数为：

(24)

为了防止BP神经网络算法对系统进行学习时陷入局部最小值[12]，增加一个全局极小的惯性项：

(25)

式中：η为学习速率；α为惯性系数。

增量式PID算法为：

u(k)=u(k-1)+kp[error(k)-error(k-1)]+

kierror(k)+kd[error(k)-2error(k-1)+

error(k-2)]

(26)

联立式(22)和式(26)，可得：

(27)

(28)

(29)

由此可得BP神经网络输出层权值的学习算法为：

(30)

3 仿真试验

本文采用传统PID控制器、改进的单神经元自适应PID控制器和BP神经网络PID控制器，分别对室内温度供热系统传递函数(14)进行仿真。

控制阶跃仿真曲线如图4所示。

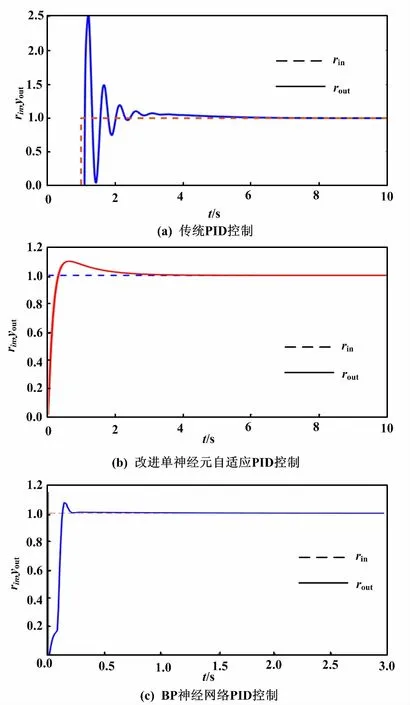
图4 控制阶跃仿真曲线Fig.4 Control step simulation curves

改进的单神经元自适应PID控制策略明显比传统PID控制策略更稳定、超调量更小。BP神经网络PID控制策略如图4(c)所示，超调量与改进的单神经元PID控制策略相比基本相同，但系统达到稳定的时间短。

为了更加精确地分析不同控制器对室内温度的控制性能，结合以上仿真结果作了性能指标分析。

性能指标分析如表1所示。

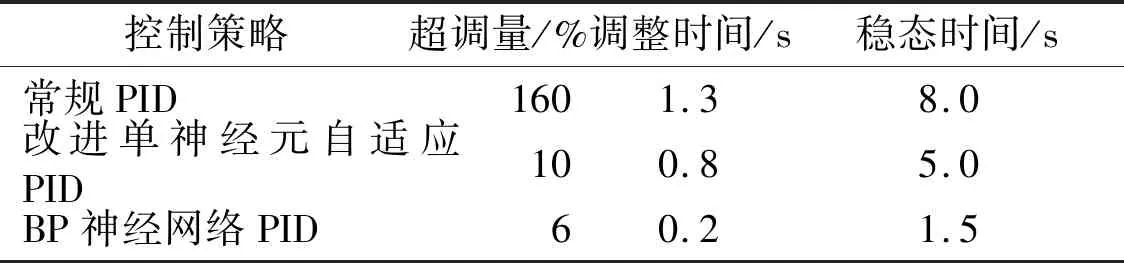
表1 性能指标分析Tab.1 Performance indicator analysis

通过表1数据可知，基于室内温度控制的不同控制策略中，BP神经网络PID控制超调量小、调整时间短、稳态时间少，其控制性能优于常规PID和改进单神经元自适应PID控制策略。

4 结束语

通过对区域集中供热系统末端用户室内温度模型的建立，进行了常规PID、改进的单神经元PID以及BP神经网络PID控制策略的室温控制仿真试验。试验结果表明，本文提出的BP神经网络PID控制策略的室温控制阶跃响应超调量小、调节时间短，达到稳态的时间最短。该BP神经网络PID控制策略可以使室内温度快速稳定在舒适的温度阈值范围内，控制效果理想。