深度学习在电力负荷预测中的应用

张建寰,吉 莹，陈立东

(厦门大学航空航天学院，福建 厦门 361000)

0 引言

负荷预测作为电力系统调度的重要组成部分，其预测精度或预测误差对电网后续运行的状态评估、安全性、经济性等具有重要意义[1-3]。随着机器学习的快速发展，目前负荷预测多采用前馈神经网络、支持向量机等机器学习技术。但由于其只是停留在浅层的学习，难以提取负荷序列的深层特征，预测精度有待进一步提升。

深度学习负荷预测领域表现出的自适应学习、感知能力，可以有效解决浅层预测模型对非线性负荷数据和多因素影响的认知能力不足，以及人为干扰等问题[4-5]。因此，为提高负荷预测的精度，本文将深度学习中的几个典型模型应用到负荷预测中，进行短期电力负荷预测，并采用常用的模型评价指标对几种模型的负荷预测进行评估和对比。

1 电力负荷预测及深度学习简介

1.1 电力负荷预测现状

电力系统的负荷预测是根据电力系统的运行特性及其他诸多因素，在满足一定精度要求下预测电力系统未来某些特定时刻的负荷数据。由于电能难以大量存储且用户端电力需求时刻变化，这就要求系统发电量要和负荷变化时刻保持动态平衡。由于负荷预测是根据过去的数值来推测未来的数值，因此负荷预测的研究对象是一个不确定、复杂的随机事件，具有不准确性、条件性、时间性和多方案性等特点。

电力负荷预测，根据其预测周期，可以分为长期、中期、短期以及超短期负荷预测。其中，短期负荷预测研究较多，其预测目标一般是预测某个地区未来一天或者一周的用电量数据。相较于其他周期的负荷预测，短期负荷预测更具实际意义，是制定发电计划和提供调度的重要参考依据。短期负荷预测的方法有很多，传统的负荷预测主要方法有：基于时间序列的自回归滑动平均模型(autoregressive moving average model,ARMA)、灰度预测和线性回归分析法等。这些模型的预测结构较为简单，应用广泛。但是它们对序列数据平稳型要求较高。大多数情况下，这些模型只是利用历史负荷数据对未来负荷进行预测，考虑因素单一，在某些情况下预测的精度会受到很大的影响。

1.2 深度学习简介

深度学习(也称为深度结构学习或逐层学习)不是特定于任务的算法，而是作为以数据学习规律为代表的、更广泛的机器学习方法系列的一部分。它的学习方式分为监督学习、半监督学习和无监督学习。作为机器学习中一个新的研究领域，它的原理是通过建立神经网络模拟人脑来分析学习，并试图模仿人脑的机制去解释事物原理。深度学习架构，比如深度神经网络、深度信念网络和递归神经网络，目前已被广泛应用到计算机视觉、图像处理、自然语言处理、语音识别、音频识别、社交网络过滤、机器翻译、生物信息学、药物设计和棋盘游戏程序等领域。机器学习的成果可与人类专家媲美，甚至在某些情况下要优于人类专家。

2 三种深度学习模型原理

2.1 LSTM神经网络原理

长短时记忆(long-short-term memory,LSTM)神经网络是一种特殊的循环神经网络(recurrent neural networks,RNN)类型，可以学习长期依赖信息。其由Hochreiter &Schmidhuber于1997年提出，近期取得了改良和推广。典型的RNN结构如图1所示。RNN神经网络内部节点定向链接成环。相比于前馈神经网络，它的本质特征是在内部的处理单元中既有反馈连接，又有前馈连接。因此，它可以利用结构的记忆功能来处理任意时间序列，更适用于不分段的手写识别或者语音识别等[6-7]。

图1 RNN结构图Fig.1 RNN structure

图1中：X为RNN神经网络的输入；h为隐含层；损失L用来衡量每个O与相应的训练目标y的距离；权重矩阵U为输入到隐藏层的权重；权重矩阵W为隐藏层到隐藏层的连接权重；权重矩阵V为隐藏层到输出层的权重矩阵。

RNN神经网络的局限性在于，随着时间间隔的不断增大，它会出现梯度消失或梯度爆炸的问题，并且其结构很容易依赖于激活函数和网络参数。基于上述问题，出现了RNN的变体LSTM神经网络[3]。LSTM典型结构如图2所示。

图2 LSTM典型结构图Fig.2 Typical LSTM structure

图2中，每条线表示一个完整的向量，即从一个节点的输出到其他节点的输入。

在标准的RNN结构中，其重复的神经网络模块的链式形式只包含一个非常简单的结构，如tanh层(如图1所示)。LSTM拥有一个不同的内部结构。它不是只有单一的神经网络层，而是有四个，并且以特殊的方式进行交互。根据图2所示，可以用以下几个公式解释LSTM循环模型单个循环体的结构。

输入门：

it=σ(Wi[ht-1,xt]+b)

(1)

遗忘门：

ft=σ(Wf[ht-1,xt]+bf)

(2)

候选时刻记忆单元：

(3)

当前时刻记忆单元：

(4)

输出门：

ot=σ(W0[ht-1,xt]+b0)

(5)

输出：

ht=ottanh(Ct)

(6)

LSTM和RNN都是利用随时间反向传播(back propagation through time,BPTT)、随机梯度或者其他算法，优化去拟合模型的最佳参数。由于LSTM更新的状态值Ct的表达式是相加的形式，因此不容易出现状态值逐渐接近0的情况，即梯度消失现象。

2.2 GRU神经网络原理

并非所有的LSTM网络结构都如图2所示。LSTM神经网络目前包含了很多的变体，其中较流行的一种是变体门循环单元(gated recurrent unit,GRU)神经网络，其结构如图3所示。它既保持了LSTM的效果，又使得结构更为简单。LSTM实现了三个门(遗忘门、输入门和输出门)的计算，而GRU实现了更新门和重置门的计算，即图3中的Zt和γt。

图3 GRU结构图Fig.3 GRU structure

GRU的前向传播方式为：

r1=σ(Wr[ht-1,xt])

(7)

zt=σ(Wz[ht-1,xt])

(8)

(9)

(10)

yt=σ(W0ht)

(11)

2.3 SAE编码器原理

自编码器(autoencoder，AE)是构建栈式自编码器(stacked auto-encoder,SAE)模型的基本单元，通过编码和解码两个功能去逼近一个使得输出接近于输入的恒等函数。自编码器结构如图4所示。其包含可视层、隐藏层和重构可视层，是一个类似于三层神经网络的结构[8]。

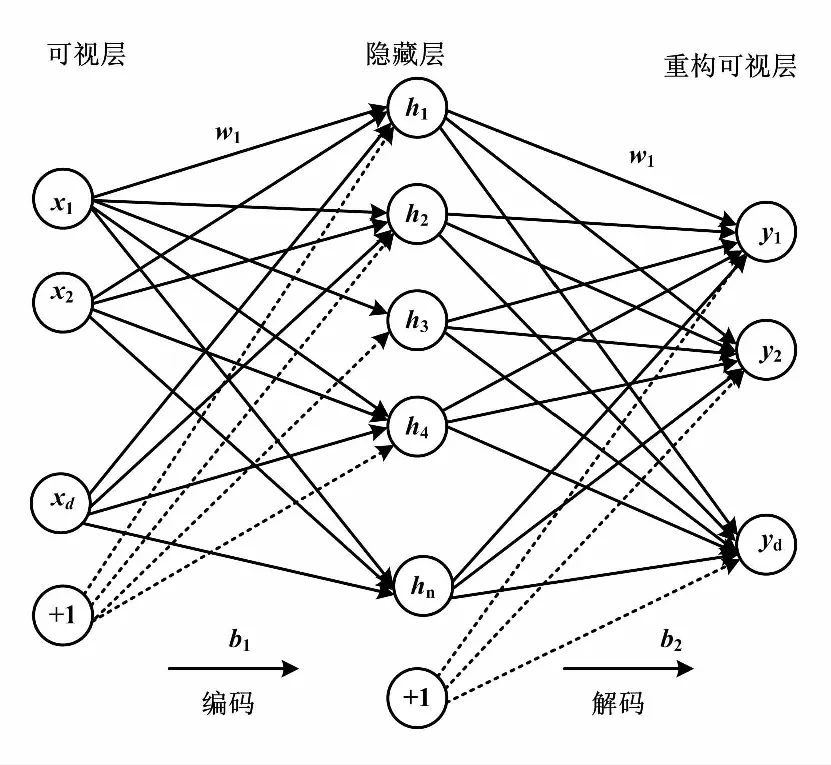
图4 自编码器结构图Fig.4 AE structure

在编码阶段，将Xi作为特征向量输入到隐藏层中，通过式(12)完成特征提取，得出编码结果h；然后使用式(13)隐含层输出结果进行解码重构，输出解码结果y(xi)。

h=f(w1xi+b1)

(12)

y(xi)=g(w2h+b2)

(13)

式(12)、式(13)中，w1和w2分别表示可视层与隐藏层、隐藏层与重构可视层的连接权值矩阵，b1和b2分别表示可视层与隐藏层、隐藏层与重构可视层的偏置值矩阵。f()和g()是对应节点的变换函数，一般采用sigmoid函数。单个自编码器通过反向传播算法训练网络，以最小化损失函数L来求解满足逼近条件y(xi)≈xi的参数{w,b}的值。自编码器损失函数C可表示为：

(14)

从图4可以发现，每个单元输入层与输出层的神经元数量相等。在实际使用中，SAE是由多个AE自编码器叠加起来的，并且逐个训练。只不过从第二个自编码器开始，其输入向量就变成了前一个编码器的隐藏层。

SAE模型结构如图5所示。其中，虚线框的结构在SAE堆叠模型结构中不出现。

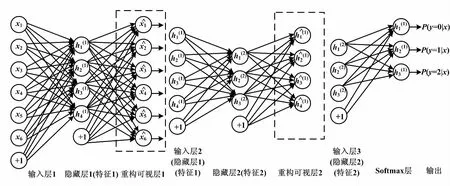
图5 SAE模型结构图Fig.5 SAE model structure

3 负荷预测模型建立

3.1 数据预处理

目前，电网系统系统收集了大量的电量信息，但是仍不可避免地存在数据缺失或者数据异常的情况[5]。如果这些数据不加以处理直接输入神经网络预测模型，必然会导致很大的误差。因此，需要对缺失的数据进行填补，并对异常数据进行识别和修正。这就是数据预处理所要做的工作[9-10]。

(1)异常数据的识别和修正处理。

正常情况下，电力负荷数据都是连续平滑的，相邻时刻点的负荷数据值不会相差太大。如果差距明显很大，那就可能是异常数据。本文中对异常数据采取水平处理方法修正，具体修正方法如下。

如果：

max[|Y(d,t)-Y(d,t-1)|,|(Y(d,t)-

Y(d,t+1)|]>ε(t)

(15)

那么：

(16)

式中：ε为阈值；t为采样的时间点。

本文中的数据是每隔半小时的数据，因此t的取值范围为1～48，Y(d,t+1)表示第d天(t+1)时刻的电力负荷值。

(2)缺失数据的补充。

考虑到负荷数据的周期性，本文对负荷数据中意外丢失的数据作拉格朗日插值法处理。

(3)数据样本归一化。

归一化操作的公式为：

(17)

式中:P为预处理后的输入样本矩阵；Pd为归一化处理后的数据矩阵；Pmax为历时输入数据中的最大值；Pmin为历时输入数据中的最小值。

3.2 建立基于负荷预测的深度学习模型

本次试验中，采用的数据样本为某地区2016年整年的负荷数据，采样周期为每半小时一次。将预处理后的数据分别输入构建的LSTM、GRU和SAE模型中。

LSTM和GRU按照正常的RNN网络进行训练。由于电脑硬件的限制，在模型的训练中，LSTM 和GRU模型都只设计了两个隐藏层，SAE模型中构建了三个单独的自动编码器。

自编码器训练的原理如前文所述，就是通过encode层对输入进行编码，即提取特征；然后，用encode层参数的转置成特征矩阵再加偏置值矩阵，以此重构输入；最后，利用最小化重构的输入和实际输入值的损失函数训练模型参数。SAE的训练过程是多个AE分别训练，第一个AE训练完以后，其输出作为第二个AE的输入，以此类推。训练完成后，将所有AE的隐藏层连接起来，就组成了SAE网络模型。按照之前各自AE训练好的权值作为初始化权值，对整个网络进行参数微调，优化全局网络参数。

3.3 预测结果分析

本文采用了平均绝对误差(mean absolute error,MAE)、均方根误差(root mean square error,RMSE)、相对百分误差绝对值的平均值(mean absolute percentage error,MAPE)、R平方(R2)和可释方差得分(explained_variance_score)这五个指标,分别对模型的预测结果进行评估和对比。

(18)

(19)

(20)

explained_variance_score[y(i),h(x(i)]=

(21)

式中:h(x(i))为网络输出的预测值；y(i)为实际负荷值。

本文以三种算法模型作为对比算法，分别将2016年一整年的负荷数据和2015～2016年两年负荷数据输入模型，对比各个模型的预测结果。编码实现基于Python3.6平台完成。表1展示了三个算法模型以2016全年数据训练模型的负荷预测指标评估结果，表2展示了三个算法模型以2015～2016数据训练模型的负荷预测指标评估结果。

表1 负荷预测指标评估结果(2016)Tab.1 Evaluation results of load forecasting indicators (2016)

表2 负荷预测指标评估结果(2015～2016)Tab.2 Evaluation results of load forecasting indicators (2015～2016)

由表1和表2可知，无论是对于负荷的长期预测还是短期预测，LSTM预测算法各个指标评价结果均优于其他预测模型。当以2016年的负荷数据作为训练样本时，LSTM负荷预测的预测误差达到5.34%；当以2015至2016两年的负荷数据作为训练样本时，LSTM负荷预测的误差可以降低至4.98%。

但由结果可知，当数据数据类型只有历史负荷数据时，三种模型的负荷预测效果都不是很理想，误差皆超过3%。其主要原因是影响负荷的因素有很多，例如节假日、气候状况、温度等。因此，进行负荷预测时，如果只考虑历史负荷数据，误差会相对较大。但是通过以上三个模型的预测结果评估对比可知，LSTM 预测模型更适用于负荷预测，并且输入的历史负荷训练数据时间越长，越有利于提高模型的预测准确度。在下一步工作中，考虑以LSTM模型作为基础进行改进，并对输入数据加入更多的特征(例如温度、气候、节假日等)，以提高负荷的预测精度。

4 结束语

电力系统的海量负荷数据为电网负荷的特性分析和高准确度、复杂的预测模型的奠定了基础。传统的负荷预测模型的结构较为简单，且考虑因素单一。而前馈神经网络、支持向量机等机器学习技术只是停留在浅层的学习，难以提取负荷序列的深层特征，模型的泛化性受到了限制，预测精度有待进一步提升。因此，本文将深度学习算法模型应用到负荷预测领域，主要对比了LSTM、GRU和SAE三种算法的预测效果，并通过对比预测精度来挖掘较为适合负荷预测的基础模型。在今后的研究中，会研究更多影响负荷预测的因素，并将其输入到神经网络模型中，以优化负荷预测模型的结构、提高预测精度；同时，考虑加入更多的顶层预训练器，以实现更精准的负荷预测。